Open Exercises
Всего страниц найдено: 51.
Задача «Задачи/eupce-2-13-b»©
Решите обобщенную версию задачи [[../eupce-2-13]]:
- kn различных купонов, организованных в n непересекающихся наборов из k купонов.
- нужен один купон из каждого набора.
Задача зарезервирована: MordashovAP 14:41, 20 декабря 2024 (UTC)
Задача «Задачи/NTIME-NlogN-reduction-3SAT»©
Покажите, что для любого языка , можно построить полиномиальную Карп-сводимость, от слов длины n, к 3SAT-формулам длины .
Задача зарезервирована: Nikitashapovalov 00:04, 20 декабря 2024 (UTC)
Задача «Задачи/DHAM3»©
Пусть
- — задача поиска гамильтонового цикла в графе , где V — делиться на 3.
- — задача подтверждения наличия гамильтонового цикла в таком графе.
Докажите, что и — NP-трудны.
Задача зарезервирована: Nikitashapovalov 00:03, 20 декабря 2024 (UTC)
Задача «Задачи/conp-as-yes»©
Покажите, что язык L лежит в co-NP тогда и только тогда, если существует недетерминированная машина M, и полином p, такой, что M останавливается за время p(n) для всех входов x длины n, и L состоит точно только из таких строк x, у которых все пути вычисления M(x) приводят к ответу «1».
Задача зарезервирована: Nikitashapovalov 23:59, 19 декабря 2024 (UTC)
Задача «Задачи/Свойство Sigma i=PH»©
.
Задача зарезервирована: Nikitashapovalov 23:54, 19 декабря 2024 (UTC)
Задача «Задачи/unary-in-p-then-time2kn-in-time2cn»©
Докажите, что если каждый унарный язык из NP также лежит в P, то то для любого языка из для какого-либо k, он тажке лежит в для любого c.
Задача зарезервирована: Nikitashapovalov 23:51, 19 декабря 2024 (UTC)
Задача «Задачи/Квадрат букв»©
Задача зарезервирована: илья52 21:51, 19 декабря 2024 (UTC)
Задача «Задачи/eupce-6-9»©
Задача зарезервирована: илья52 21:50, 19 декабря 2024 (UTC)
Задача «Задачи/eupce-6-20»©
Задача зарезервирована: илья52 21:49, 19 декабря 2024 (UTC)
Задача «Задачи/eupce-1-16-d»©
Задача зарезервирована: илья52 21:49, 19 декабря 2024 (UTC)
Рассмотрим игру, основанную на бросках трех стандартных шестисторонних костей. Цель → получить одинаковое число на всех трех костях, кто первый этого добьется, тот выиграл.
- Игрок начинает с броска всех трех кубиков.
- После первого броска игрок может выбрать одну, две или три кости и бросить их снова.
- После второго броска игрок один из трех кубиков и перебросить его.
Предположим, что игрок использует следующую оптимальную стратегию:
- если все три кости одинаковые → останавливаемся и выигрываем;
- если два кубика совпадают, игрок перебрасывает тот, который «выбивается из коллектива».
- если все не совпадают — перебрасываем их всех.
Рассматривая все возможные возможные выпадения костей, найдите вероятность того, что игрок выиграет.
Задача «Задачи/eupce-6-14»©
Задача зарезервирована: илья52 21:25, 19 декабря 2024 (UTC)
Задача «Задачи/eupce-6-2-a»©
Задача зарезервирована: NikitaAkshaev 15:11, 19 декабря 2024 (UTC)
Докажите, что для каждого целого числа n существует раскраска ребер полного графа в два цвета, такое что полное число одноцветных подграфов будете не больше чем
Задача «Задачи/eupce-1-16-a»©
Рассмотрим игру, основанную на бросках трех стандартных шестисторонних костей.
Цель → получить одинаковое число на всех трех костях, кто первый этого добьется, тот выиграл.
- Игрок начинает с броска всех трех кубиков.
- После первого броска игрок может выбрать одну, две или три кости и бросить их снова.
- После второго броска игрок один из трех кубиков и перебросить его.
Предположим, что игрок использует следующую оптимальную стратегию:
- если все три кости одинаковые → останавливаемся и выигрываем;
- если два кубика совпадают, игрок перебрасывает тот, который «выбивается из коллектива».
- если все не совпадают — перебрасываем их всех.
Найдите вероятность того, что все три кубика показывают одинаковое число в первом броске.
Задача зарезервирована: MordashovAP 12:37, 19 декабря 2024 (UTC)
Задача «Задачи/eupce-1-26-b»©
Обычные крестики-нолики скучные, при оптимальной стратегии в них выигрывают крестики.
Рассмотрим вероятную модификацию этой игры.
- Как обычно, крестики и нолики ходят по очереди и нолик идет первым. Как обычно, выигрывает тот, кто первый добъется «три в ряд», или ничья, если никто.
- Но на каждом ходе позиция и у крестиков и у ноликов выбирается независимо и равномерно среди свободных квадратов.
Найдите вероятность, выигрыша для «крестиков» и для «ноликов».
Задача зарезервирована: MordashovAP 12:33, 19 декабря 2024 (UTC)
Задача «Задачи/P^BPP»©
Какой класс будет
Задача зарезервирована: NikitaAkshaev 11:40, 18 декабря 2024 (UTC)
Задача «Задачи/eupce-6-1-a»©
Рассмотрим K-ESAT, SAT, когда в каждой скобке ровно k литералов.
Предложите Лас-Вегас алгоритм выполняющий минимум
скобок, и проанализируйте матожидание его времени выполнения.
Задача зарезервирована: NikitaAkshaev 11:28, 18 декабря 2024 (UTC)
Задача «Задачи/eupce-6-10»©
Задача зарезервирована: Trifonov.dv 19:15, 15 декабря 2024 (UTC)
Задача «Задачи/eupce-6-7»©
Задача зарезервирована: Glbmkrv 02:35, 15 декабря 2024 (UTC)
Задача «Задачи/eupce-2-7-a»©
X и Y — независимые случайные величины с геометрическим распределением, с параметрами P и Q соответственно.
P(X = Y) = ?
Задача зарезервирована: Галлямов Ислам М05-304б 15:36, 13 декабря 2024 (UTC)
Задача «Задачи/eupce-1-14»©
Задача зарезервирована: Ydanyok 15:32, 13 декабря 2024 (UTC)
Я играю в турнире ракетбола против игрока, против которого раньше не играл, но видел его в игре.
Априори рассматриваю три равновероятные возможности:
- мы одинаково талантливы, каждый из нас в равной степени может выиграть каждую игру;
- Я немного лучше, и поэтому я выигрываю каждую игру независимо с вероятностью 0.6;
- Он немного лучше, и поэтому он выигрывает каждую игру независимо с вероятностью 0.6.
В рокетбол играют, пока один игрок не выиграет три сета. В нашей игре, я выиграл только второй сет, а противник выиграл первый, третий и четвертый.
В апостеорной модели, с какой вероятностью я должен верить, что мой оппонент немного лучше, чем я?
Задача «Задачи/accept-after-t-steps-in-npc»©
Задача зарезервирована: Ydanyok 09:10, 13 декабря 2024 (UTC)
- M
- одноленточная машина Тьюринга над бинарным алфавитом.
- t
- число t единичной системе (t единиц).
- Существует вход x, M(x) останавливается и возвращает 1, после t шагов.
Покажите, что это NP-полная задача.
Задача «Задачи/Жадное вершинное покрытие для почти всех исходных данных»©
Задача зарезервирована: Ydanyok 09:03, 13 декабря 2024 (UTC)
- n-вершин
- ребра между любой парой вершин возникают с вероятностью p.
Какова точность алгоритма для почти всех исходных данных?
(упрощенный вариант — для фиксированного p=½).
Задача «Задачи/eupce-1-26-a»©
Задача зарезервирована: Ydanyok 09:03, 13 декабря 2024 (UTC)
Обычные крестики-нолики скучные, при оптимальной стратегии в них выигрывают крестики. Рассмотрим вероятную модификацию этой игры.
- Изначально, бросая честную монетку, разметим каждый из девяти квадратов либо X, либо O.
- Если только один из игроков имеет «три в ряд» → он победил.
- Если оба или никто → ничья.
Определите вероятность, что «X» выиграет.
Задача «Задачи/eupce-2-9»©
Задача зарезервирована: Галлямов Ислам М05-304б 13:43, 9 декабря 2024 (UTC)
Дважды бросают честный k-гранный кубик с числами от 1 от k до k на гранях кубика, получая значения X1 и X2.
- E[max(X1, X2)] = ?
- E[min(X1, X2)] = ?
Покажите, что E[max(X1 , X2)] + E[min(X1 , X2)] = E[X1] + E[X2].
Задача «Задачи/eupce-2-6-d»©
Предположим, что независимо бросают два стандартных шестисторонних кости, X1 — то, что выпадает на первой, X2 — на второй, а X — сумма обоих значений.
- 2 ≤ k ≤ 12
- E[X1 - X2 | X = k] = ?
Задача зарезервирована: RomanFilonov 20:42, 8 декабря 2024 (UTC)
Задача «Задачи/eupce-1-11-c»©
Пытаемся передать один бит (0 или 1) через «n» промежуточных узлов, каждый из которых независимо
может инвертировать бит с вероятностью «p».
Докажите, что вероятность получения корректного бита:
Задача зарезервирована: RomanFilonov 19:10, 8 декабря 2024 (UTC)
Задача «Задачи/eupce-1-9»©
- Честную монету бросили «n» раз.
- Для k>0, найдите верхнюю границу вероятности, что будет последовательность из последовательных орлов.
Задача зарезервирована: RomanFilonov 15:46, 8 декабря 2024 (UTC)
Задача «Задачи/eupce-6-8»©
Задача зарезервирована: Конин Георгий 20:59, 3 декабря 2024 (UTC)
Задача «Задачи/eupce-6-11»©
Задача зарезервирована: AlferovIS 20:54, 1 декабря 2024 (UTC)
Задача «Задачи/eupce-2-6-c»©
Предположим, что независимо бросают два стандартных шестисторонних кости, X1 — то, что выпадает на первой, X2 — на второй, а X — сумма обоих значений.
E[X1 | X = 9] = ?
Задача зарезервирована: AlferovIS 16:19, 1 декабря 2024 (UTC)
Задача «Задачи/eupce-2-13»©
- Каждая коробка хлопьев содержит один из 2n различных купонов (купон в каждой коробке выбирается независимо и равномерно случайным образом из 2n).
- Купоны организованы в n пар, так что купоны 1 и 2 составляют пару, купоны 3 и 4 составляют пару и так далее.
- Получив по одному купону из каждой пары, вы можете получить приз.
Какое ожидаемое количество коробок, надо для этого купить?
Задача зарезервирована: AlferovIS 16:11, 1 декабря 2024 (UTC)
Задача «Задачи/eupce-2-5»©
Если X — случайная величина с биномиальным распределением B(n, 1/2) для n ≥ 1, покажите, что вероятность того,
что X — четное будет 1/2.
Задача зарезервирована: AlferovIS 16:09, 1 декабря 2024 (UTC)
Задача «Задачи/eupce-2-6-b»©
Предположим, что независимо бросают два стандартных шестисторонних кости, X1 — то, что выпадает на первой, X2 — на второй, а X — сумма обоих значений.
E[X | X1 = X2] = ?
Задача зарезервирована: LunevLA 15:06, 25 ноября 2024 (UTC)
Задача «Задачи/NP-sums»©
Проверить принадлежность классу следующей задачи: по заданному конечному множеству натуральных чисел, представленных в своей бинарной записи, определить возможность разделения этого множества на два подмножества с одинаковыми суммами.
Задача зарезервирована: LunevLA 16:01, 23 ноября 2024 (UTC)
Задача «Задачи/eupce-2-8-a»©
Алиса и Боб решили заводить детей до тех пор, пока у них не родится девочка или пока у них не будет k ≥ 1 детей.
Предположим, что каждый ребенок будет мальчиком или девочкой независимо с вероятностью 1/2 и что многоплодных родов не бывает.
- Каково ожидаемое число детей женского пола?
- Каково ожидаемое число детей мужского пола?
Задача зарезервирована: LunevLA 15:45, 23 ноября 2024 (UTC)
Задача «Задачи/eupce-6-15»©
Задача зарезервирована: EjenY 15:43, 10 ноября 2024 (UTC)
Задача «Задачи/eupce-2-7-c»©
Задача зарезервирована: Solovev 15:16, 10 ноября 2024 (UTC)
X и Y — независимые случайные величины с геометрическим распределением, с параметрами P и Q соответственно.
P(min(X, Y) = k) = ?
Задача «Задачи/eupce-2-4»©
Докажите, что для любого целого .
Задача зарезервирована: Ermakov
Задача «Задачи/eupce-1-13»©
Медицинская компания рекламирует свой новый тест на определенное заболевание.
Частота ошибок первого рода (false negative) мала: если у вас есть расстройство, вероятность того, что тест вернет положительный результат, составляет 0.999.
Частота ошибок второго рода (false positive) тоже невелика: если у вас нет расстройства, вероятность того, что тест вернет положительный результат, составляет всего 0.005.
Предположим, что эту болезнь имеет 2% населения.
Если мы проверяем человека, выбранного равномерно из популяции, и получается положительный результат, какова вероятность того, что эта болезнь у него действительно есть?
Задача зарезервирована: Ermakov
Задача «Задачи/eupce-1-15»©
Предположим, что бросают десять стандартных шестисторонних костей.
Какова вероятность того, что их сумма будет деленной на 6, предполагая, что броски независимы?
Задача зарезервирована: Ermakov
Задача «Задачи/MAX-CUT-NPC»©
Докажите, что задача MAX-CUT, в форме задачи разрешения («правда, ли, что для графа G есть разрез больше K?») NP-полна.
Задача зарезервирована: Ermakov
Задача «Задачи/eupce-6-1-b»©
Предложите алгоритм дерандомизации методом условных вероятностей для алгоритма из MAX-SAT: вероятностное округление/Задачи/eupce-6-1-a.
Задача «Задачи/eupce-1-18»©
- Есть функция
- и известно что .
Единственный способ вычисления F — использовать таблицу поиска, в которой хранится значения F. К сожалению, злой противник изменил значение 1/5 записей в этой таблице.
Опишите простой рандомизированный алгоритм, который, учитывая входной Z, выводит значение, которое равняется f(z) с вероятностью не менее 1/2.
Ваш алгоритм должен работать для каждого значения Z, независимо от того, какие записи изменил противник.
Дополнительно, предположим, вам разрешено повторить этот ваш начальный алгоритм три раза.
Как этим воспрользоваться, чтобы максимально увеличить вероятность правильного ответа, и какова эта вероятность?
Задача «Задачи/\Sigma^p k=NP^(\Sigma^p (k-1))»©
Докажите
Задача «Задачи/QBEQ-NPC-NPC»©
Покажите NP-полноту языка совместимых систем квадратичных уравнений в булевых переменных. Т.е. разрешимых систем вида
и где сложение по модулю 2.
Задача «Задачи/USUBSETSUM-IN-P»©
Вспомним задачу булев-рюкзак выполнимость, и потребуем, чтобы все веса и размер рюкзака задавались в унарной системе ().
Покажите, что тогда язык таких выполнимых рюкзаков, лежит в классе P.
Задача «Задачи/scheduling-ident-machines-in-npc»©
Рассмотрим задачу разрешения для оптимизационной задачи Планирование Задач на Одинаковых Машинах («если ли планировка с максимальным временем меньше k»).
Покажите, что эта задача, даже в случае p=2, NP-полна.
Задача «Задачи/Порядок закачек — NPC»©
Представим распределенный сервис стриминга видеофильмов. Центральный сервер с полной БД фильмов получает от периферийных кеширующих узлов запросы на требуемые фильмы и ориентировочные сроки, когда люди собираются их посмотреть.
Однако пропускная способность от сервера с дисками к внешнему миру ограничена, и требуется составить работающее расписание отгрузки фильмов.
Конкретно, узел контроля планирования получает n-заданий вида:
- «начать_не_раньше, закончить_не_позже, размер_фильма»i, 1<=i<=n
- максимальная пропускная способность не больше МаксКанал
И говорит «OK» (или «Паника-Паника!» в противном случае), если существует такое расписание из n команд отгрузки, соответствующих заданию (1<=i<=n ):
- «время_начала, время_окончания, ширина_канала»i,
- время_началаi >= начать_не_раньшеi
- время окончанияi <= закончить_не_позжеi
- ширина_каналаi <= МаксКанал
- ширина_канала*(время_окончания — время_начала)i >= размер_фильмаi
Докажите NP-полноту задачи.
Hint: Можно через «Рюкзак-выполнимость» или «SUBSET-SUM»
Задача «Задачи/ptas-for-minimal-scheduling»©
Разработайте PTAS-алгоритм для Планирование Задач на Одинаковых Машинах используя этот подход.
Задача «Задачи/maximum-k-choice-knapsack-dynamic-programming»©
Придумайте алгоритм динамического программирования, находящий оптимальное решение задачи Maximum Integer k-choice Knapsack.
Задача «Задачи/P^(\Sigma^p k)=P^(\Pi^p k)»©
Докажите
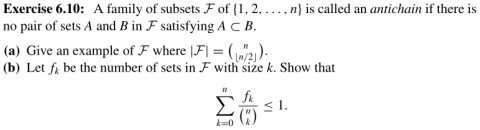
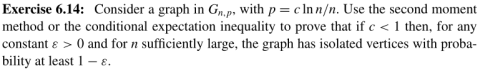
[ Хронологический вид ]Комментарии
Войдите, чтобы комментировать.