Python-оптимизация жадного алгоритма из codechef
StasFomin (обсуждение | вклад) |
StasFomin (обсуждение | вклад) |
||
| (не показано 14 промежуточных версий этого же участника) | |||
| Строка 5: | Строка 5: | ||
{{oldid|1=chefstr2.py|2=20542|3=Первая версия}} | {{oldid|1=chefstr2.py|2=20542|3=Первая версия}} | ||
| − | Видимо легкий перебор, | + | Видимо легкий перебор, три вложенных цикла (три цикла, что-то дофига, причем явно с зависимостью от длины входа — не к добру), что-то считается, что-то отбирается по максимуму…, суммируется, отбирается по минимуму — типичный жадный алгоритм. |
Cмотрим описание задачи [[Codechef/CHEFSTR2]], даже сразу переходим по ссылке [https://discuss.codechef.com/t/chefstr2-editorial/83721 на разбор и разъяснение]. | Cмотрим описание задачи [[Codechef/CHEFSTR2]], даже сразу переходим по ссылке [https://discuss.codechef.com/t/chefstr2-editorial/83721 на разбор и разъяснение]. | ||
| − | Разьяснение немного мутное, и мутность там даже зачем-то подмешивается во входные данные (вторая строчка входа не нужна). Но суть простая, есть строка, хотим из нее сделать какую-то повторяющуюся подстроку меньшего размера, можем менять символы и добавлять к концу произвольные, но нужно минимизировать число таких операций. | + | Разьяснение немного мутное, и мутность там даже зачем-то подмешивается во входные данные (вторая строчка входа не нужна). |
| + | |||
| + | Но суть простая, есть строка, хотим из нее сделать какую-то повторяющуюся подстроку меньшего размера, можем менять символы и добавлять к концу произвольные, но нужно минимизировать число таких операций. | ||
Вот, нарисовал картинку в терминах исходной версии программы: | Вот, нарисовал картинку в терминах исходной версии программы: | ||
| − | [[File:chefstr2.svg|800px|center]] | + | [[File:Python-оптимизация жадного алгоритма из codechef_2022-05-05_12-39-25_image0.png|center|800px]] |
| + | <!-- [[File:chefstr2.svg|800px|center]] --> | ||
| + | Мы можем попробовать делать циклы из подстрок разной длины («ind»), повторяющиеся разное число раз «ks», чтобы получилась строка, нужной длины или чуть длиннее (не больше чем на «ind»). | ||
| + | ---- | ||
| − | + | Рассмотрим строку «ABCABCAB». | |
| − | + | ||
| − | + | Если делать цикл из одного символа («ind=1, ks=8»), то на «пути» (красным) надо посчитать частоты символов, выбрать самый частый (пусть он остается), остальные поменять на него — оптимальное жадное решение. Тут можно выбрать «А» или «B» и получить <m>(A)^8</m> или <m>(B)^8</m>. | |
| + | Сколько операций переименования-добавления? Это будет «len» символов новой строки с повторами, минус те символы, которых мы не переименуем («ok», три символа «A» или «B»). | ||
| + | Будет 5 операций. (Если оставлять «C», то их будет 6, не подоходит). | ||
| − | + | ---- | |
| − | + | Если делать цикл из двух символов («ind=2, ks=4»), то у нас уже возникают «красный» и «синий» путь — пути для первого и второго символа, на этих путях должны быть одинаковые символы, они совсем независимы, надо на каждом пути посчитать какой символ наиболее часто встречается, и переименовать все остальные в него. | |
| − | |||
| − | + | На красном пути — самый частый → «A», на синем → «B». Значит, на «красном» пути оставим «A», остальных переименуем в него, на «синем» → «B». На обоих путях одинаково число оставляемых символов «ok1=2», «ok2=2» → число операций | |
| − | + | ops = len - ok1 - ok2 = 8 - 2 - 2 = 4 | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | |||
| − | + | ---- | |
| − | + | Если делать цикл из трех символов («ind=3, ks=3»), то у нас уже возникают «красный», «синий» и зеленый пути — пути от первого, второго и третьего символа … | |
| − | + | … обратите внимание, что зеленый путь выходит за пределы исходной строки, т.е. один символ по любому придется добавить, ведь длина зацикленной строки «len = ks*ind = 9» больше длины исходной строки («8»). | |
| − | + | ||
| − | + | ||
| − | + | На красном пути — самый частый → «A», на синем → «B», на зеленом → «С» Значит, на «красном» пути оставим «A», остальных переименуем в него, на «синем» → «B», на зеленом → «С». | |
| − | + | ops = len - ok1 - ok2 - ok3 = 9 - 3 - 3 - 2 = 1 | |
| − | + | ||
| − | + | … | |
| − | + | ||
| − | + | можно продолжать дальше, в [https://discuss.codechef.com/t/chefstr2-editorial/83721 разъяснении] написано, почему «ind» не обязательно перебирать до исходной длины строки, идея понятна, у меня кончились красивые цвета для путей. | |
| − | + | Разумеется, из всех вариантов циклов с разной длинной надо будет выбрать тот, где «ops» — минимально. | |
| − | + | ---- | |
| − | + | ||
| − | + | Итак, поехали. Пишем генератор тестовой строки | |
| − | |||
<source lang="python"> | <source lang="python"> | ||
| − | + | import random | |
| − | + | import string | |
| + | |||
| + | print(''.join((random.choice(string.ascii_letters).lower() for i in range(16000)))) | ||
| + | print(1) | ||
</source> | </source> | ||
| − | + | генерим «big-sample-04.txt» на 16K символов, | |
| + | берем референсный CPP-код из разъяснения, компилируем. | ||
| − | + | <pre> | |
| + | gcc -o good good.cpp -lstdc++ -g | ||
| + | </pre> | ||
| + | <pre> | ||
| + | $ time good < big-sample-04.txt | ||
| + | 7671 2 | ||
| − | + | real 0m47.380s | |
| + | user 0m46.872s | ||
| + | sys 0m0.053s | ||
| + | </pre> | ||
| − | + | Работать будем сразу с PyPy3, не будем тащить numpy, какие-нибудь хитрые модули подсчета, и даже не будем использовать Counter из collections, хотя он сюда и напрашивается. | |
| − | + | <pre> | |
| − | + | $ time pypy3 chefstr2.py < big-sample-04.txt | |
| + | 7671 2 | ||
| − | + | real 0m26.806s | |
| + | user 0m26.286s | ||
| + | sys 0m0.104s | ||
| + | </pre> | ||
| − | + | {{@|26.2}} секунды. | |
| − | + | Вау, забавно. Это решение вроде как копия референсного на CPP, а на PyPy работает быстрее. | |
| + | Но по TL не проходит! | ||
| − | + | Нет, пока чудес не бывает. Компилим CPP код с оптимизацией | |
| − | + | gcc -o good good.cpp -lstdc++ -O3 | |
| − | + | ||
| − | + | и после этого наконец-то сишное решение показывает скорость: | |
| − | + | ||
| − | + | <pre> | |
| + | $ time good < big-sample-04.txt | ||
| + | 7671 2 | ||
| − | + | real 0m1.968s | |
| − | + | user 0m1.947s | |
| − | + | sys 0m0.006s | |
| − | + | </pre> | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | Итак, правильное решение знаем, можем проверить, есть куда стремится по скорости. | |
| + | Первое, что напрягает — зачем нам тут модуль «math», вещественные числа (ересь! у нас тут честная комбинаторика). Только для того, чтобы округлять вверх? Это можно делать [https://stackoverflow.com/questions/14822184/is-there-a-ceiling-equivalent-of-operator-in-python не выходя из целых чисел]. | ||
| − | |||
| − | + | Делаем {{diff| 20555 | такие правки}} и получаем версию работающую за {{!|24.5}} — чуть лучше. | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | Для очистки совести | |
| − | + | {{diff| 20557 | уберем хардкод на 26 символов и прочтем входную строку через sys.readline}} — {{@|26.6}} стало даже чуть хуже, но вроде это более надежный ввод, если запускать на серверах кодечифа. | |
| − | + | ||
| − | + | Что еще напрягает? Ну вот зачем такие глубокие косвенности: | |
| − | + | frequency[symbols[(input_str[j])]] | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | * Давайте {{diff| 20559 | сразу переведем строку в байт-массив индексов символов, и будем работать с ним }} → {{!|13.7}} — почти в два раза! | |
| − | + | ||
| − | + | ||
| − | + | * Давайте {{diff| 20562 | не уныло обнулять вектор частот, а сразу выделять новый забитый нулями }} → {{!|13.1}}. | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | * Попытка {{diff| 20564 | поставить более вероятную ветку в первый «if» не помогла }} → {{@|13.1}}. | |
| − | + | ||
| − | + | ||
| − | + | * А вот континтуитивное — {{diff| 20567 | заменяем стандартный поиск максимального элемента на корявое поддержание «максимальной текущей частоты»}} → {{@|9.3}}. Тут выигрыш скорее всего за счет того, что на «длинных путях» у нас массив частот становится разряженным, и максимальную частоту дешевле считать так, чем бегать по всему массиву. | |
| + | * А может, если у нас чувствуется разряженность, {{diff| 20569 | перейти с списка частот на хеш?}} → {{@|13.4}}. Не помогает, стало хуже. | ||
| − | + | Пора подумать внимательно, зачем нам так много нужно вложенных циклов. | |
| − | + | * Внешний цикл по длинам подстрок — ладно, пусть остается. | |
| + | * А два внутренних — по сути, подсчет «частот символов на разноцветных путях», и расчет из этого количества операций. Давайте заменим это на один цикл, по самой строке (вернее по массиву индексов символов), и для каждого индекса, будем решать, частоту какого символа (из «lenalf» символов) и на каком «пути» (из «ind» возможных путей) он увеличивает. {{diff| 20571 | Заводим списки векторы frequency — по сути, двухмерный массив, который моделируем одномерным списком, и массив max_frequency}} → {{!|9.1}} удивительно! Выигрыш есть, но совсем небольшой. А ведь еще мы память тратим, но вроде тут она бесплатна<ref>Не надо так весело разбрасываясь памятью оптимизировать в продакшне реальных проектов, если действительно этот размен не будет оправдан!</ref>. | ||
| + | * {{diff| 20573 | От огорчения убрал sys и вернул input }} — не повлияло. | ||
| − | [ | + | Пробуем загрузить решение в СС → увы, [https://www.codechef.com/viewsolution/64250087 TL] |
| − | + | Ночь, хочеться спать.... и тут оживают Дьявольские Советы Черного Программиста → стоит подумать — а в чем практическая задача нашего кода? | |
| − | + | Пройти приемочные испытания! Показать себя хорошо на реальных входных данных. | |
| − | + | Будут ли среди них такие плохие данные, ради которых стоит перестраховываться и увеличивать перебор? (по сути, можно считать, мы исследуем переход к вероятностным алгоритмам или «эффективности для почти всех исходных данных»). | |
| + | * {{diff| 20575 | Подкручиваем-уменьшаем перебор! }} — и наше [https://www.codechef.com/viewsolution/64250125 решение подходит], даже с хорошим запасом! | ||
| + | Возможно конечно когда-нибудь в этой задаче дополнят тест-сет, и это решение не пройдет… так что оставим как челлендж на «отл» (при условии, что есть «одна теоретическая задача») → | ||
| + | * сделать питон решение (без машинных кодов), которое проходит тесты, но перебирет все циклы до 0.75*n | ||
| + | ** ну либо обосновать, что действительно, можно опустить верхнюю оценку максимальной длины цикла в переборе. | ||
| + | Челледж на «хор» → подобрать входные данные, на которых [https://www.codechef.com/viewsolution/64250125 вот это решение даст неправильный результат]. | ||
| + | {{wl-publish: 2022-05-05 00:01:56 +0000 | StasFomin }} | ||
---- | ---- | ||
| − | |||
Текущая версия на 09:39, 5 мая 2022
Продолжим тему Blog:Advanced Algorithms/Python-оптимизация алгоритма динамического программирования из codechef.
Итак, снова решение, которое вроде как работает, но не проходит по времени и жалобы, что питон плохой «Получаю TimeLimit в системе. Мне кажется, это связано с тем, что использую питон и в решении очень много численных операций а так как в питоне используются BigInteger BigFloats, то решение замедляется».
Видимо легкий перебор, три вложенных цикла (три цикла, что-то дофига, причем явно с зависимостью от длины входа — не к добру), что-то считается, что-то отбирается по максимуму…, суммируется, отбирается по минимуму — типичный жадный алгоритм.
Cмотрим описание задачи Codechef/CHEFSTR2, даже сразу переходим по ссылке на разбор и разъяснение.
Разьяснение немного мутное, и мутность там даже зачем-то подмешивается во входные данные (вторая строчка входа не нужна).
Но суть простая, есть строка, хотим из нее сделать какую-то повторяющуюся подстроку меньшего размера, можем менять символы и добавлять к концу произвольные, но нужно минимизировать число таких операций.
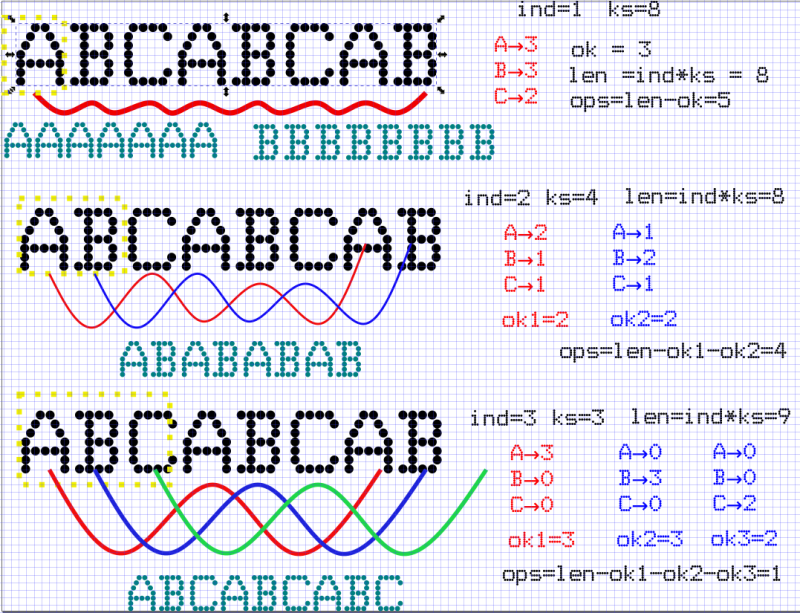
Вот, нарисовал картинку в терминах исходной версии программы:
Мы можем попробовать делать циклы из подстрок разной длины («ind»), повторяющиеся разное число раз «ks», чтобы получилась строка, нужной длины или чуть длиннее (не больше чем на «ind»).
Рассмотрим строку «ABCABCAB».
Если делать цикл из одного символа («ind=1, ks=8»), то на «пути» (красным) надо посчитать частоты символов, выбрать самый частый (пусть он остается), остальные поменять на него — оптимальное жадное решение. Тут можно выбрать «А» или «B» и получить или . Сколько операций переименования-добавления? Это будет «len» символов новой строки с повторами, минус те символы, которых мы не переименуем («ok», три символа «A» или «B»). Будет 5 операций. (Если оставлять «C», то их будет 6, не подоходит).
Если делать цикл из двух символов («ind=2, ks=4»), то у нас уже возникают «красный» и «синий» путь — пути для первого и второго символа, на этих путях должны быть одинаковые символы, они совсем независимы, надо на каждом пути посчитать какой символ наиболее часто встречается, и переименовать все остальные в него.
На красном пути — самый частый → «A», на синем → «B». Значит, на «красном» пути оставим «A», остальных переименуем в него, на «синем» → «B». На обоих путях одинаково число оставляемых символов «ok1=2», «ok2=2» → число операций
ops = len - ok1 - ok2 = 8 - 2 - 2 = 4
Если делать цикл из трех символов («ind=3, ks=3»), то у нас уже возникают «красный», «синий» и зеленый пути — пути от первого, второго и третьего символа … … обратите внимание, что зеленый путь выходит за пределы исходной строки, т.е. один символ по любому придется добавить, ведь длина зацикленной строки «len = ks*ind = 9» больше длины исходной строки («8»).
На красном пути — самый частый → «A», на синем → «B», на зеленом → «С» Значит, на «красном» пути оставим «A», остальных переименуем в него, на «синем» → «B», на зеленом → «С».
ops = len - ok1 - ok2 - ok3 = 9 - 3 - 3 - 2 = 1
…
можно продолжать дальше, в разъяснении написано, почему «ind» не обязательно перебирать до исходной длины строки, идея понятна, у меня кончились красивые цвета для путей.
Разумеется, из всех вариантов циклов с разной длинной надо будет выбрать тот, где «ops» — минимально.
Итак, поехали. Пишем генератор тестовой строки
import random import string print(''.join((random.choice(string.ascii_letters).lower() for i in range(16000)))) print(1)
генерим «big-sample-04.txt» на 16K символов, берем референсный CPP-код из разъяснения, компилируем.
gcc -o good good.cpp -lstdc++ -g
$ time good < big-sample-04.txt 7671 2 real 0m47.380s user 0m46.872s sys 0m0.053s
Работать будем сразу с PyPy3, не будем тащить numpy, какие-нибудь хитрые модули подсчета, и даже не будем использовать Counter из collections, хотя он сюда и напрашивается.
$ time pypy3 chefstr2.py < big-sample-04.txt 7671 2 real 0m26.806s user 0m26.286s sys 0m0.104s
26.2 секунды.
Вау, забавно. Это решение вроде как копия референсного на CPP, а на PyPy работает быстрее. Но по TL не проходит!
Нет, пока чудес не бывает. Компилим CPP код с оптимизацией
gcc -o good good.cpp -lstdc++ -O3
и после этого наконец-то сишное решение показывает скорость:
$ time good < big-sample-04.txt 7671 2 real 0m1.968s user 0m1.947s sys 0m0.006s
Итак, правильное решение знаем, можем проверить, есть куда стремится по скорости. Первое, что напрягает — зачем нам тут модуль «math», вещественные числа (ересь! у нас тут честная комбинаторика). Только для того, чтобы округлять вверх? Это можно делать не выходя из целых чисел.
Делаем такие правки и получаем версию работающую за 24.5 — чуть лучше.
Для очистки совести уберем хардкод на 26 символов и прочтем входную строку через sys.readline — 26.6 стало даже чуть хуже, но вроде это более надежный ввод, если запускать на серверах кодечифа.
Что еще напрягает? Ну вот зачем такие глубокие косвенности:
frequency[symbols[(input_str[j])]]
- Давайте сразу переведем строку в байт-массив индексов символов, и будем работать с ним → 13.7 — почти в два раза!
- Попытка поставить более вероятную ветку в первый «if» не помогла → 13.1.
- А вот континтуитивное — заменяем стандартный поиск максимального элемента на корявое поддержание «максимальной текущей частоты» → 9.3. Тут выигрыш скорее всего за счет того, что на «длинных путях» у нас массив частот становится разряженным, и максимальную частоту дешевле считать так, чем бегать по всему массиву.
- А может, если у нас чувствуется разряженность, перейти с списка частот на хеш? → 13.4. Не помогает, стало хуже.
Пора подумать внимательно, зачем нам так много нужно вложенных циклов.
- Внешний цикл по длинам подстрок — ладно, пусть остается.
- А два внутренних — по сути, подсчет «частот символов на разноцветных путях», и расчет из этого количества операций. Давайте заменим это на один цикл, по самой строке (вернее по массиву индексов символов), и для каждого индекса, будем решать, частоту какого символа (из «lenalf» символов) и на каком «пути» (из «ind» возможных путей) он увеличивает. Заводим списки векторы frequency — по сути, двухмерный массив, который моделируем одномерным списком, и массив max_frequency → 9.1 удивительно! Выигрыш есть, но совсем небольшой. А ведь еще мы память тратим, но вроде тут она бесплатна[1].
- От огорчения убрал sys и вернул input — не повлияло.
Пробуем загрузить решение в СС → увы, TL
Ночь, хочеться спать.... и тут оживают Дьявольские Советы Черного Программиста → стоит подумать — а в чем практическая задача нашего кода?
Пройти приемочные испытания! Показать себя хорошо на реальных входных данных. Будут ли среди них такие плохие данные, ради которых стоит перестраховываться и увеличивать перебор? (по сути, можно считать, мы исследуем переход к вероятностным алгоритмам или «эффективности для почти всех исходных данных»).
- Подкручиваем-уменьшаем перебор! — и наше решение подходит, даже с хорошим запасом!
Возможно конечно когда-нибудь в этой задаче дополнят тест-сет, и это решение не пройдет… так что оставим как челлендж на «отл» (при условии, что есть «одна теоретическая задача») →
- сделать питон решение (без машинных кодов), которое проходит тесты, но перебирет все циклы до 0.75*n
- ну либо обосновать, что действительно, можно опустить верхнюю оценку максимальной длины цикла в переборе.
Челледж на «хор» → подобрать входные данные, на которых вот это решение даст неправильный результат.
- ↑ Не надо так весело разбрасываясь памятью оптимизировать в продакшне реальных проектов, если действительно этот размен не будет оправдан!