Optprob/Иголка в стоге сена — различия между версиями
StasFomin (обсуждение | вклад) (Массовая правка: замена Категория:OptimizationProblems на {{Cat4Term2|{{FULLPAGENAME}}|OptimizationProblems}}) |
StasFomin (обсуждение | вклад) |
||
| (не показана одна промежуточная версия этого же участника) | |||
| Строка 11: | Строка 11: | ||
«[http://lib.custis.ru/%C2%AB%D0%A3%D0%BF%D1%80%D0%B0%D0%B2%D0%BB%D0%B5%D0%BD%D0%B8%D0%B5_%D0%BF%D1%80%D0%BE%D0%B8%D0%B7%D0%B2%D0%BE%D0%B4%D1%81%D1%82%D0%B2%D0%BE%D0%BC_%D0%BD%D0%B0_%D0%BE%D1%81%D0%BD%D0%BE%D0%B2%D0%B0%D0%BD%D0%B8%D0%B8_%D1%87%D0%B8%D1%81%D0%BB%D0%B5%D0%BD%D0%BD%D1%8B%D1%85_%D0%B4%D0%B0%D0%BD%D0%BD%D1%8B%D1%85%C2%BB_%D0%B8_%C2%AB%D0%A2%D0%B5%D0%BE%D1%80%D0%B8%D1%8F_%D0%BE%D0%B3%D1%80%D0%B0%D0%BD%D0%B8%D1%87%D0%B5%D0%BD%D0%B8%D0%B9_%D0%B8_%D0%BB%D0%B8%D0%BD%D0%B5%D0%B9%D0%BD%D0%BE%D0%B5_%D0%BF%D1%80%D0%BE%D0%B3%D1%80%D0%B0%D0%BC%D0%BC%D0%B8%D1%80%D0%BE%D0%B2%D0%B0%D0%BD%D0%B8%D0%B5%C2%BB_(2009-08-03) Синдроме Стога Сена]» на 40 страницах текста без малейшей романтики и лирики рассматривается в цифрах оптимизация некоторого модельного производства, и где «на пальцах» читателя убеждают, что для достижения максимальной прибыли нужно жертвовать локальными оптимумами, и принимать решения, часто интуитивно непонятные. Эту книгу десятилетия любят бизнес-тренеры, и консультанты, перерабатывают ее в тренинги…, см. например, | «[http://lib.custis.ru/%C2%AB%D0%A3%D0%BF%D1%80%D0%B0%D0%B2%D0%BB%D0%B5%D0%BD%D0%B8%D0%B5_%D0%BF%D1%80%D0%BE%D0%B8%D0%B7%D0%B2%D0%BE%D0%B4%D1%81%D1%82%D0%B2%D0%BE%D0%BC_%D0%BD%D0%B0_%D0%BE%D1%81%D0%BD%D0%BE%D0%B2%D0%B0%D0%BD%D0%B8%D0%B8_%D1%87%D0%B8%D1%81%D0%BB%D0%B5%D0%BD%D0%BD%D1%8B%D1%85_%D0%B4%D0%B0%D0%BD%D0%BD%D1%8B%D1%85%C2%BB_%D0%B8_%C2%AB%D0%A2%D0%B5%D0%BE%D1%80%D0%B8%D1%8F_%D0%BE%D0%B3%D1%80%D0%B0%D0%BD%D0%B8%D1%87%D0%B5%D0%BD%D0%B8%D0%B9_%D0%B8_%D0%BB%D0%B8%D0%BD%D0%B5%D0%B9%D0%BD%D0%BE%D0%B5_%D0%BF%D1%80%D0%BE%D0%B3%D1%80%D0%B0%D0%BC%D0%BC%D0%B8%D1%80%D0%BE%D0%B2%D0%B0%D0%BD%D0%B8%D0%B5%C2%BB_(2009-08-03) Синдроме Стога Сена]» на 40 страницах текста без малейшей романтики и лирики рассматривается в цифрах оптимизация некоторого модельного производства, и где «на пальцах» читателя убеждают, что для достижения максимальной прибыли нужно жертвовать локальными оптимумами, и принимать решения, часто интуитивно непонятные. Эту книгу десятилетия любят бизнес-тренеры, и консультанты, перерабатывают ее в тренинги…, см. например, | ||
[http://lib.custis.ru/Toc-lp тренинг Сергея Мартыненко] или вот (→→→), свежий пост из бизнесового телеграмм-чата | [http://lib.custis.ru/Toc-lp тренинг Сергея Мартыненко] или вот (→→→), свежий пост из бизнесового телеграмм-чата | ||
| − | |||
| − | |||
Но если попробовать честно математически сформулировать эту задачу, выясняется, что даже сам Голдратт, пропустил оптимальное решение. | Но если попробовать честно математически сформулировать эту задачу, выясняется, что даже сам Голдратт, пропустил оптимальное решение. | ||
| Строка 23: | Строка 21: | ||
* [[Участник:Larin.dv/Иголка в стоге сена]] | * [[Участник:Larin.dv/Иголка в стоге сена]] | ||
| + | {{optsolv|Иголка_в_стоге_сена}} | ||
| + | {{vim|783966486}} | ||
{{enddiv}} | {{enddiv}} | ||
| − | |||
{{Cat4Term2|{{FULLPAGENAME}}|OptimizationProblems}} | {{Cat4Term2|{{FULLPAGENAME}}|OptimizationProblems}} | ||
Текущая версия на 01:28, 6 октября 2024
Создатель «теории ограничений» и пропагандист математической оптимизации в бизнес-задачах Элияху Моше Голдратт, часто прибегал к написанию «производственных бизнес-романов» для иллюстрации своих идей.
Очень рекомендую, для культуры, прочитать хотя бы первый и самый известный роман — «Цель»
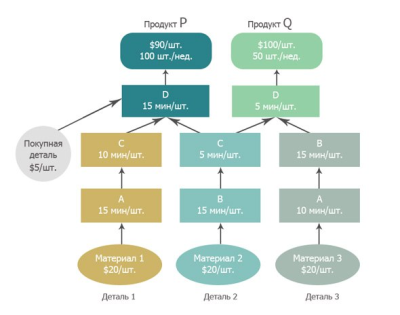
В одном из них, в «Синдроме Стога Сена» на 40 страницах текста без малейшей романтики и лирики рассматривается в цифрах оптимизация некоторого модельного производства, и где «на пальцах» читателя убеждают, что для достижения максимальной прибыли нужно жертвовать локальными оптимумами, и принимать решения, часто интуитивно непонятные. Эту книгу десятилетия любят бизнес-тренеры, и консультанты, перерабатывают ее в тренинги…, см. например, тренинг Сергея Мартыненко или вот (→→→), свежий пост из бизнесового телеграмм-чата
Но если попробовать честно математически сформулировать эту задачу, выясняется, что даже сам Голдратт, пропустил оптимальное решение. В докладе Стас Фомина была приведена модель на MathML и решение на GLPK (увы, вроде остались только слайды и видео), надо повторить это на Pyomo. Может где-то ее уже на Pyomo и решили (не проверял).
Всю книгу там перечитывать не обязательно, но если прочитаете — это будет совсем незря!