2011-gre-cs-practice-book.pdf/Q11 — различия между версиями
Материал из DISCOPAL
Urmat A (обсуждение | вклад) |
Urmat A (обсуждение | вклад) |
||
| Строка 1: | Строка 1: | ||
| − | {{reserve-task|[[Участник:Urmat A|Urmat A]] 15: | + | {{reserve-task|[[Участник:Urmat A|Urmat A]] 15:59, 18 декабря 2024 (UTC)}} |
== Вопрос: Q11-08c765 == | == Вопрос: Q11-08c765 == | ||
| Строка 19: | Строка 19: | ||
[[File:NPstuff.png|320px]] | [[File:NPstuff.png|320px]] | ||
| + | |||
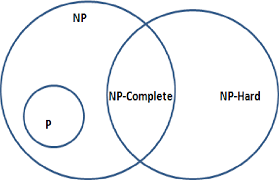
Взглянем на картинку и разберем: | Взглянем на картинку и разберем: | ||
#если задача A NP-полная и для нее существует полиномиальный алгоритм, то действительно P=NP | #если задача A NP-полная и для нее существует полиномиальный алгоритм, то действительно P=NP | ||
Версия 15:59, 18 декабря 2024
Задача зарезервирована: Urmat A 15:59, 18 декабря 2024 (UTC)
Вопрос: Q11-08c765
Предположим, что задача A является NP-полной, а задача B находится в NP, но не обязательно NP-полной. Какое из следующих утверждений обязательно верно?
- . Полиномиальный алгоритм для A подразумевает P = NP.
- . Полиномиальный алгоритм для B подразумевает P = NP.
- . Полиномиальный алгоритм для A подразумевает полиномиальный алгоритм для B
Ответы
- только 1
- только 2
- только 1 и 2
- Правильный ответ: только 1 и 3
- 1, 2 и 3
Объяснение
Исходники — вопрос 11 на 20 странице книги «2011-gre-cs-practice-book.pdf»
Взглянем на картинку и разберем:
- если задача A NP-полная и для нее существует полиномиальный алгоритм, то действительно P=NP
- если задача B в NP, но необязательно в классе NP-полных и для нее существует полиномиальный алгоритм, то это все равно есть задачи из класса NP-полных, поэтому равенство P=NP не выполняется
- Если A лежит в классе NP-полных и для нее существует полиномиальный алгоритм, то и для всего NP тоже существует полиномиальный алгоритм, то есть для B тоже