2011-gre-cs-practice-book.pdf/Q16 — различия между версиями
Материал из DISCOPAL
Urmat A (обсуждение | вклад) (→Вопрос: Q16-08c765) |
StasFomin (обсуждение | вклад) |
||
| Строка 1: | Строка 1: | ||
| − | |||
| − | |||
| − | |||
| − | |||
== Вопрос: Q16-08c765 == | == Вопрос: Q16-08c765 == | ||
| Строка 8: | Строка 4: | ||
=== Ответы === | === Ответы === | ||
| − | + | * 250 | |
| − | + | * Правильный ответ: 499 | |
| − | + | * 500 | |
| − | + | * 501 | |
| − | + | * 1000 | |
=== Объяснение === | === Объяснение === | ||
| Строка 18: | Строка 14: | ||
{{cstest-source|2011-gre-cs-practice-book.pdf|22|16}} | {{cstest-source|2011-gre-cs-practice-book.pdf|22|16}} | ||
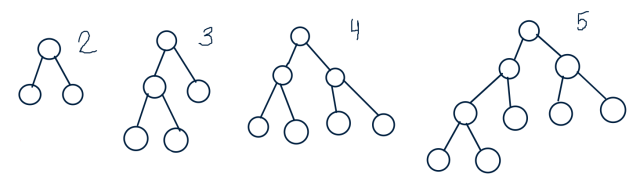
| − | Проиллюстрируем на картинке: | + | Проиллюстрируем на картинке: |
[[Файл:Full Binary Heap.png|640px]] | [[Файл:Full Binary Heap.png|640px]] | ||
| − | Начнём с первого дерева у которого два листа. Далее, если мы хотим прибавить +1 лист к дереву, то мы дорисовываем по 2 потомка свободным листам, беря их слева направо. Таким образом количество листьев всегда на 1 больше количества внутренних узлов | + | * Начнём с первого дерева у которого два листа. |
| − | + | * Далее, если мы хотим прибавить +1 лист к дереву, то мы дорисовываем по 2 потомка свободным листам, беря их слева направо. | |
| + | * Таким образом количество листьев всегда на 1 больше количества внутренних узлов | ||
| − | {{question-ok|}} | + | {{question-ok|[[Участник:StasFomin|StasFomin]] 21:08, 18 декабря 2024 (UTC)}} |
| − | + | [[Категория:Структуры данных]] | |
Текущая версия на 21:08, 18 декабря 2024
Вопрос: Q16-08c765
Полное бинарное дерево — это корневое дерево, в котором каждый внутренний узел имеет ровно два потомка. Сколько внутренних узлов в полном бинарном дереве с 500 листьями?
Ответы
- 250
- Правильный ответ: 499
- 500
- 501
- 1000
Объяснение
Исходники — вопрос 16 на 22 странице книги «2011-gre-cs-practice-book.pdf»
- Начнём с первого дерева у которого два листа.
- Далее, если мы хотим прибавить +1 лист к дереву, то мы дорисовываем по 2 потомка свободным листам, беря их слева направо.
- Таким образом количество листьев всегда на 1 больше количества внутренних узлов