2001-gre-math.pdf/Q23 — различия между версиями
Материал из DISCOPAL
(→Вопрос: Q23-19def7) |
StasFomin (обсуждение | вклад) |
||
| (не показаны 2 промежуточные версии этого же участника) | |||
| Строка 1: | Строка 1: | ||
| − | |||
| − | |||
| − | |||
== Вопрос: Q23-19def7 == | == Вопрос: Q23-19def7 == | ||
| − | |||
На евклидовой плоскости точка A находится на окружности с центром в точке O, а O - на окружности с центром в точке A. | На евклидовой плоскости точка A находится на окружности с центром в точке O, а O - на окружности с центром в точке A. | ||
Окружности пересекаются в точках B и C. Какова градусная мера угла BAC? | Окружности пересекаются в точках B и C. Какова градусная мера угла BAC? | ||
| Строка 16: | Строка 12: | ||
=== Объяснение === | === Объяснение === | ||
| − | + | [[File:Q23_2025-01-06_21-00-45_image0.png|480px|right]] | |
{{cstest-source|2001-gre-math.pdf|26|23}} | {{cstest-source|2001-gre-math.pdf|26|23}} | ||
| − | + | * BO=AO как радиусы окружности с центром в точке O; | |
| − | + | * BA=AO как радиусы окружности с центром в точке A. | |
| − | BO=AO как радиусы окружности с центром в точке O; BA=AO как радиусы окружности с центром в точке A. Значит, треугольник OBA равносторонний, все углы в нем по 60°. Аналогично, треугольник OCA равносторонний и все углы в нем по 60°. Угол BAC равен сумме углов BAO и CAO, следовательно, равен 120°. | + | * Значит, треугольник OBA равносторонний, все углы в нем по 60°. |
| + | * Аналогично, треугольник OCA равносторонний и все углы в нем по 60°. | ||
| + | * Угол BAC равен сумме углов BAO и CAO, следовательно, равен 120°. | ||
| − | {{question-ok|}} | + | {{question-ok|[[Участник:StasFomin|StasFomin]] 20:17, 6 января 2025 (UTC)}} |
[[Категория:Математика]] | [[Категория:Математика]] | ||
Текущая версия на 20:18, 6 января 2025
Вопрос: Q23-19def7
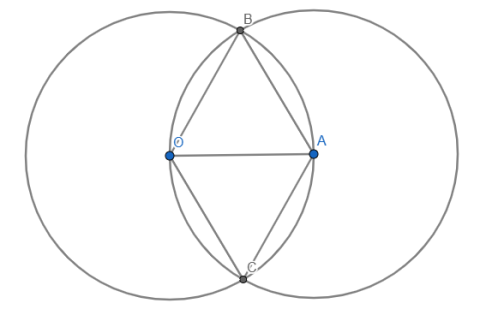
На евклидовой плоскости точка A находится на окружности с центром в точке O, а O - на окружности с центром в точке A. Окружности пересекаются в точках B и C. Какова градусная мера угла BAC?
Ответы
- 60°
- 90°
- Правильный ответ: 120°
- 135°
- 150°
Объяснение
Исходники — вопрос 23 на 26 странице книги «2001-gre-math.pdf»
- BO=AO как радиусы окружности с центром в точке O;
- BA=AO как радиусы окружности с центром в точке A.
- Значит, треугольник OBA равносторонний, все углы в нем по 60°.
- Аналогично, треугольник OCA равносторонний и все углы в нем по 60°.
- Угол BAC равен сумме углов BAO и CAO, следовательно, равен 120°.