2011-gre-cs-practice-book.pdf/Q21 — различия между версиями
Материал из DISCOPAL
StasFomin (обсуждение | вклад) (Новая страница: « == Вопрос: Q21-08c765 == <i>Тут вставьте перевод вопроса. Используйте [https://wiki.4intra.net/Help:%D0%A4%D0%BE%D1%80…») |
StasFomin (обсуждение | вклад) |
||
| (не показано 6 промежуточных версий 2 участников) | |||
| Строка 1: | Строка 1: | ||
| − | |||
== Вопрос: Q21-08c765 == | == Вопрос: Q21-08c765 == | ||
| − | + | [[File:bintree.png|320px]] | |
| − | + | <!-- | |
| − | + | Как бы графвизом рисовать неполное бинарное дерево? | |
| − | + | <graph> | |
| + | digraph G{ | ||
| + | 5->3 | ||
| + | 5->9 | ||
| + | 3->1 | ||
| + | 3->4 | ||
| + | 9->7 | ||
| + | } | ||
| + | </graph> | ||
| + | --> | ||
| − | + | Начиная с пустого двоичного дерева поиска, вставка какой из следующих последовательностей целочисленных ключей | |
| − | + | может создать двоичное дерево выше? | |
| − | + | ||
| − | + | ||
=== Ответы === | === Ответы === | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | * 5, 9, 1, 7, 3, 4 | ||
| + | * 5, 7, 4, 9, 3, 1 | ||
| + | * 5, 4, 7, 3, 9, 1 | ||
| + | * Правильный ответ: 5, 3, 4, 9, 1, 7 | ||
| + | * 5, 3, 1, 7, 9, 4 | ||
=== Объяснение === | === Объяснение === | ||
| − | + | {{cstest-source|2011-gre-cs-practice-book.pdf|25|21}} | |
| − | {{cstest-source|2011-gre-cs-practice-book.pdf| | + | |
| − | + | ||
| − | + | ||
| − | + | Дерево строится так, что все потомки левее предка меньше него, и все потомки правее предка больше него по значению. | |
| − | + | * Начинаем с 5. | |
| − | + | * Далее подойдет 3 или 9. Поэтому варианты «5, 7, 4, 9, 3, 1» и «5, 4, 7, 3, 9, 1» отпадают. | |
| + | * Вариант «5, 9, 1, 7, 3, 4» не подходит, так как 1 была бы прямым потомком 5. | ||
| + | * Вариант «5, 9, 1, 7, 3, 4» тоже отпал. после 5-3-1 не может быть 7, ведь она тоже была бы прямым потомком 5. | ||
| + | * Вариант «5, 3, 4, 9, 1, 7» подходит идеально. | ||
| − | + | {{question-ok|[[Участник:StasFomin|StasFomin]] 21:41, 18 декабря 2024 (UTC)}} | |
| − | + | [[Категория:Структуры данных]] | |
Текущая версия на 21:43, 18 декабря 2024
Вопрос: Q21-08c765
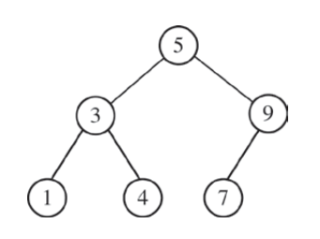
Начиная с пустого двоичного дерева поиска, вставка какой из следующих последовательностей целочисленных ключей может создать двоичное дерево выше?
Ответы
- 5, 9, 1, 7, 3, 4
- 5, 7, 4, 9, 3, 1
- 5, 4, 7, 3, 9, 1
- Правильный ответ: 5, 3, 4, 9, 1, 7
- 5, 3, 1, 7, 9, 4
Объяснение
Исходники — вопрос 21 на 25 странице книги «2011-gre-cs-practice-book.pdf»
Дерево строится так, что все потомки левее предка меньше него, и все потомки правее предка больше него по значению.
- Начинаем с 5.
- Далее подойдет 3 или 9. Поэтому варианты «5, 7, 4, 9, 3, 1» и «5, 4, 7, 3, 9, 1» отпадают.
- Вариант «5, 9, 1, 7, 3, 4» не подходит, так как 1 была бы прямым потомком 5.
- Вариант «5, 9, 1, 7, 3, 4» тоже отпал. после 5-3-1 не может быть 7, ведь она тоже была бы прямым потомком 5.
- Вариант «5, 3, 4, 9, 1, 7» подходит идеально.