2004-gre-cs-practice-book.pdf/Q67 — различия между версиями
Материал из DISCOPAL
StasFomin (обсуждение | вклад) |
StasFomin (обсуждение | вклад) |
||
| (не показана одна промежуточная версия этого же участника) | |||
| Строка 26: | Строка 26: | ||
R(n) = R(n-1) + n | R(n) = R(n-1) + n | ||
</m> | </m> | ||
| − | → <m>\frac{ | + | → <m>R(n) = \frac{n \left(n + 1\right)}{2} + 1</m> |
<code-python> | <code-python> | ||
from sympy import * | from sympy import * | ||
| − | + | R = Function('R') | |
n = symbols('n', integer=True, positive=True) | n = symbols('n', integer=True, positive=True) | ||
| − | recurrence = | + | recurrence = R(n) - R(n-1) - n |
| − | rsolve(recurrence, | + | rsolve(recurrence, R(n), {R(0):1, R(1):2}) |
| − | # print(latex(rsolve(recurrence, | + | # print(latex(rsolve(recurrence, R(n), {R(0):1, R(1):2}))) |
</code-python> | </code-python> | ||
| − | {{question-ok | + | {{question-ok|[[Участник:StasFomin|StasFomin]] 09:40, 16 декабря 2024 (UTC)}} |
| − | + | ||
| − | + | ||
Текущая версия на 10:45, 16 декабря 2024
Вопрос: Q67-4c9f66
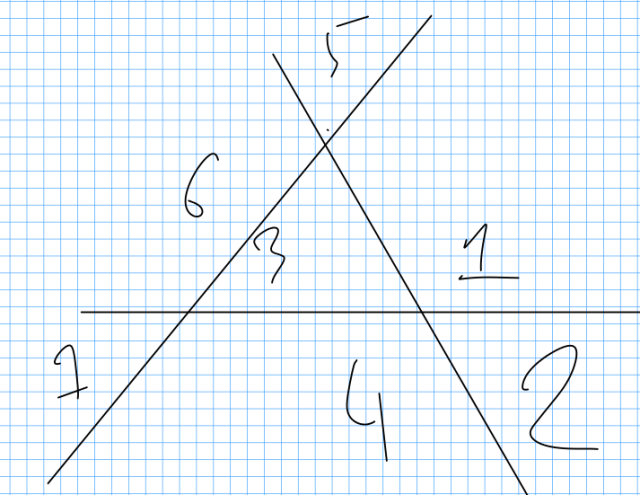
Для каждого неотрицательного целого числа n пусть — максимально возможное число областей, на которые плоскость может быть разделена n прямыми линиями.
Например, и
Тогда имеет порядок
Ответы
- Правильный ответ:
Объяснение
Исходники — вопрос 67 на 43 странице книги «2004-gre-cs-practice-book.pdf»
Каждая новая прямая n пересекает предыдущие n-1 прямую, порождая n новых областей.
Тут явно надо будет решить рекурентное уравнение.
→
from sympy import * R = Function('R') n = symbols('n', integer=True, positive=True) recurrence = R(n) - R(n-1) - n rsolve(recurrence, R(n), {R(0):1, R(1):2}) # print(latex(rsolve(recurrence, R(n), {R(0):1, R(1):2})))