2008-gre-math-0568.pdf/Q05 — различия между версиями
Материал из DISCOPAL
StasFomin (обсуждение | вклад) |
StasFomin (обсуждение | вклад) |
||
| (не показаны 4 промежуточные версии 2 участников) | |||
| Строка 1: | Строка 1: | ||
== Вопрос: Q05-ed3507 == | == Вопрос: Q05-ed3507 == | ||
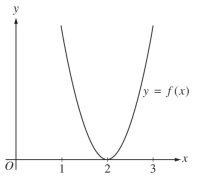
| + | Пусть <m>b</m> — действительное число, и <m>f(x) = 3x^2 + bx + 12</m> — функция, часть которой изображена на рисунке ниже. Тогда <m>f(5)=</m> | ||
| − | + | [[File:Q05_2025-01-08_16-40-00_image0.png|200px]] | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
=== Ответы === | === Ответы === | ||
| − | < | + | * <m>15</m> |
| − | + | * Правильный ответ: <m>27</m> | |
| − | + | * <m>67</m> | |
| − | * Правильный ответ: | + | * <m>72</m> |
| − | * | + | * <m>87</m> |
| − | * | + | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | < | + | |
| − | + | ||
| − | + | ||
| − | + | ||
=== Объяснение === | === Объяснение === | ||
| − | + | {{cstest-source|2008-gre-math-0568.pdf|14|5}} | |
| − | {{cstest-source|2008-gre-math-0568.pdf| | + | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
<code-python> | <code-python> | ||
from sympy import * | from sympy import * | ||
| + | x, b = symbols('x b') | ||
| + | f = 3*x**2 + b*x + 12 | ||
| + | real_b = solve(f.subs(x, 2), b)[0] | ||
| + | f_explicit = 3*x**2 + real_b*x + 12 | ||
| + | f_explicit.subs(x, 5) | ||
</code-python> | </code-python> | ||
| − | + | {{question-ok|[[Участник:StasFomin|StasFomin]] 19:23, 8 января 2025 (UTC)}} | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | {{question-ok|}} | + | |
[[Категория:Математика]] | [[Категория:Математика]] | ||
Текущая версия на 19:23, 8 января 2025
Вопрос: Q05-ed3507
Пусть — действительное число, и — функция, часть которой изображена на рисунке ниже. Тогда
Ответы
- Правильный ответ:
Объяснение
Исходники — вопрос 5 на 14 странице книги «2008-gre-math-0568.pdf»
from sympy import * x, b = symbols('x b') f = 3*x**2 + b*x + 12 real_b = solve(f.subs(x, 2), b)[0] f_explicit = 3*x**2 + real_b*x + 12 f_explicit.subs(x, 5)