2001-gre-math.pdf/Q18 — различия между версиями

Материал из DISCOPAL
Перейти к: навигация, поиск
(Новая страница: « == Вопрос: Q18-19def7 == <blockquote> Тут вставьте перевод вопроса. Используйте [https://wiki.4intra.net/Help:%D0%A4%D…»)
 
 
(не показана 1 промежуточная версия 1 участника)
Строка 1: Строка 1:
−
 
 
== Вопрос: Q18-19def7 ==
 
== Вопрос: Q18-19def7 ==
  
−
<blockquote>
+
[[File:Q18_2025-01-06_21-25-52_image0.png|right]]
−
Тут вставьте перевод вопроса.
+
−
Используйте [https://wiki.4intra.net/Help:%D0%A4%D0%BE%D1%80%D0%BC%D0%B0%D1%82%D0%B8%D1%80%D0%BE%D0%B2%D0%B0%D0%BD%D0%B8%D0%B5 возможности разметки],
+
−
включая формулы и т.п, если будут графы — посмотрите как задать их текстом https://wiki.4intra.net/Graphviz (реально оценю, полезный навык).
+
  
−
В IT вообще не принято писать романы, всегда старайтесь писать структурированные (списками-абзацами тексты). Списки в MediaWiki — это просто «*». Не забывайте о них.
+
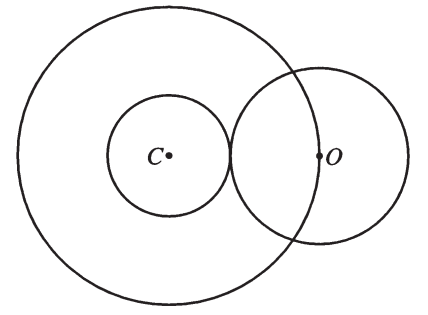
На рисунке кольцо с центром C имеет внутренний радиус r и внешний радиус 1. По мере увеличения r
−
* Преформатированный моноширинный текст — просто отступ.  
+
окружность с центром O сужается, оставаясь касательной к внутренней окружности с центром C. Пусть <m>A(r)</m> - площадь кольца, а <m>a(r)</m> - площадь круга с центром O. Найти предел <m>\[ \lim_{x\to 1-0} \frac{A(r)}{a(r)} \]</m>
−
* Короткая математика — тег <nowiki><m>\sum_i^100 i^2</m></nowiki>
+
−
* Большой LaTeX-блок (пример [[2008-gre-math-0568.pdf/Q09]])
+
−
<nowiki><latex>
+
−
… Lores ipsum $\sum_i^100 i^2$ …
+
−
</latex></nowiki>
+
−
 
+
−
Старайтесь нетривиальные понятия, особенно незнакомые вам, найти ссылку на википедию и вставить (нейросети лажают!).
+
−
Это важно, чтобы найти корректный перевод (то, что в википедии, или на худой конец — точно массово гуглится).
+
−
 
+
−
Потом конечно сотрите эти инструкции, которые тут курсивом или в блоке цитирования (и тег «blockquote»).
+
−
</blockquote>
+
  
 
=== Ответы ===
 
=== Ответы ===
−
<i>Если ответы простые, однострочные, используйте простой способ задания ответов списком, типа так
 
−
(префикс «Правильный ответ:» — это дословно, для правильного ответа, неважно, какой он будет в списке)</i>
 
  
−
* Правильный ответ: тут реально правильный ответ
+
* <m>0</m>
−
* неправильный ответ
+
* <m>\frac{2}{\pi}</m>
−
* еще какой-то неправильный ответ
+
* <m>1</m>
−
* еще какой-то неправильный ответ
+
* <m>\frac{\pi}{2}</m>
−
* еще какой-то неправильный ответ
+
* Правильный ответ: <m>\infty</m>
  
−
<i>Если ответы длинные, многострочные, или там графы, используйте
+
=== Объяснение ===
−
[https://wiki.4intra.net/MediawikiQuizzer/ru#.D0.9E.D1.82.D0.B2.D0.B5.D1.82.D1.8B способ задания ответов разделами],
+
−
Но такое очень редко встречается, например [[2011-gre-cs-practice-book.pdf/Q05]]. </i>
+
  
 +
{{cstest-source|2001-gre-math.pdf|22|18}}
  
−
=== Объяснение ===
+
<code-python>
−
<i>Сначала заполните номер страницы с этим вопросом
+
import sympy
−
{{cstest-source|2001-gre-math.pdf|тут-номер-страницы-с-вопросом-18|18}}
+
  
−
Если все сделаете правильно, по ссылке выше будет открываться правильная страница в правильном PDFе.
+
r = sympy.Symbol("r")
 +
A = sympy.pi * (1**2 - r**2)
 +
a = sympy.pi * (1 - r)**2
  
−
Ну и наконец, вики-разметкой напишите ваше понимание, почему правильный ответ — правильный, а неправильные варианты — неправильны.
+
limit_ratio = sympy.limit(A/a, r, 1, dir="-")
−
Конкретно здесь, в математических тестах ожидается в большинстве случаев просто блок питон-кода с использованием sympy,
+
−
см. [[Blog:Advanced_Algorithms/Потренируйтесь_в_sympy_на_детских_тестах_по_математике]], просто добавьте ваш код в этот тег:
+
  
−
<code-python>
+
print(limit_ratio)
−
from sympy import *
+
−
....
+
 
</code-python>
 
</code-python>
  
−
Но если уж sympy неприменим, распишите плиз, как понимаете 🤷‍♂️.
+
{{question-ok|[[Участник:StasFomin|StasFomin]] 20:15, 6 января 2025 (UTC)}}
−
</i>
+
−
 
+
−
{{question-ok|}}
+
  
−
[[Category:Математика]]
+
[[Категория:Математика]]

Текущая версия на 20:15, 6 января 2025

Вопрос: Q18-19def7

Q18 2025-01-06 21-25-52 image0.png

На рисунке кольцо с центром C имеет внутренний радиус r и внешний радиус 1. По мере увеличения r окружность с центром O сужается, оставаясь касательной к внутренней окружности с центром C. Пусть - площадь кольца, а - площадь круга с центром O. Найти предел

Ответы

  • Правильный ответ:

Объяснение

Исходники — вопрос 18 на 22 странице книги «2001-gre-math.pdf» 

import sympy
 
r = sympy.Symbol("r")
A = sympy.pi * (1**2 - r**2)
a = sympy.pi * (1 - r)**2
 
limit_ratio = sympy.limit(A/a, r, 1, dir="-")
 
print(limit_ratio)
Источник — «https://discopal.ispras.ru/index.php?title=2001-gre-math.pdf/Q18&oldid=35321»