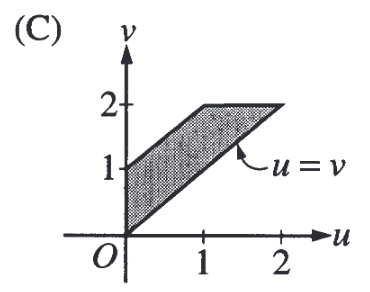2001-gre-math.pdf/Q48 — различия между версиями
Материал из DISCOPAL
(→Вопрос: Q48-19def7) |
StasFomin (обсуждение | вклад) |
||
| (не показана 1 промежуточная версия 1 участника) | |||
| Строка 1: | Строка 1: | ||
| − | |||
== Вопрос: Q48-19def7 == | == Вопрос: Q48-19def7 == | ||
| Строка 15: | Строка 14: | ||
Какой из предложенных регионов на плоскости (u, v) отображает трансформацию пространства {<math>(x, y): 0 \le x \le 1 ; 0 \le y \le 1</math>} | Какой из предложенных регионов на плоскости (u, v) отображает трансформацию пространства {<math>(x, y): 0 \le x \le 1 ; 0 \le y \le 1</math>} | ||
| − | ==== | + | ==== Правильный ответ ==== |
| + | [[Файл:a48.png]] | ||
| + | ==== Ответ ==== | ||
| + | [[Файл:b48.png]] | ||
| − | ==== Ответ ==== | + | ==== Ответ ==== |
| + | [[Файл:c48.png]] | ||
| + | ==== Ответ ==== | ||
| + | [[Файл:d48.png]] | ||
| − | ==== Ответ ==== | + | ==== Ответ ==== |
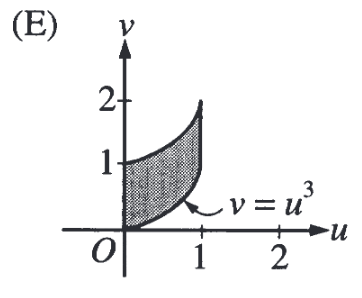
| + | [[Файл:e48.png]] | ||
| + | === Объяснение === | ||
| + | {{cstest-source|2001-gre-math.pdf|42|48}} | ||
| − | + | Можно заметить, что при заданных ограничениях на y, переменная v принимает значения от 1 до 2, значит уже можем оставить только варианты A и D. | |
| + | Далее, заметим что при фиксированном v, y = v — 1, а u принимает значения от <m>u_{min} = 0 + v - 1</m> до <m>u_{max} = v</m>. Можно заметить, что этому условию удовлетворяет вариант A. | ||
| − | + | {{question-ok|[[Участник:StasFomin|StasFomin]] 13:47, 13 января 2025 (UTC)}} | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | {{ | + | |
| − | + | ||
| − | + | ||
| − | + | ||
[[Категория:Математика]] | [[Категория:Математика]] | ||
Текущая версия на 13:47, 13 января 2025
Содержание
[убрать]Вопрос: Q48-19def7
Рассмотрим замену переменных из (x, y) плоскости в (u, v) плоскость заданную уравнениями:
Какой из предложенных регионов на плоскости (u, v) отображает трансформацию пространства {}
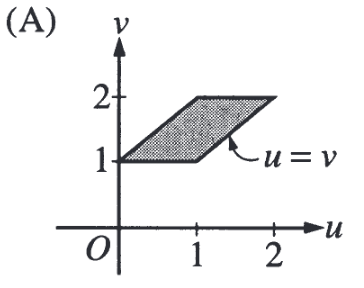
Правильный ответ
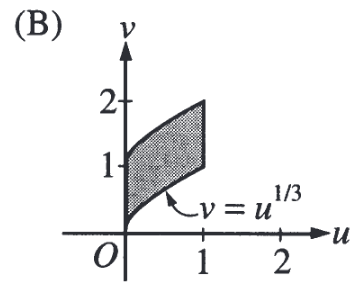
Ответ
Ответ
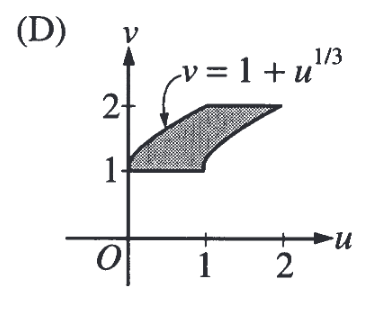
Ответ
Ответ
Объяснение
Исходники — вопрос 48 на 42 странице книги «2001-gre-math.pdf»
Можно заметить, что при заданных ограничениях на y, переменная v принимает значения от 1 до 2, значит уже можем оставить только варианты A и D.
Далее, заметим что при фиксированном v, y = v — 1, а u принимает значения от до . Можно заметить, что этому условию удовлетворяет вариант A.