2001-gre-math.pdf/Q07 — различия между версиями

Материал из DISCOPAL
Перейти к: навигация, поиск
(→‎Вопрос: Q07-19def7)
(→‎Вопрос: Q07-19def7)
Строка 2: Строка 2:
 
== Вопрос: Q07-19def7 ==
 
== Вопрос: Q07-19def7 ==
  
−
<blockquote>
+
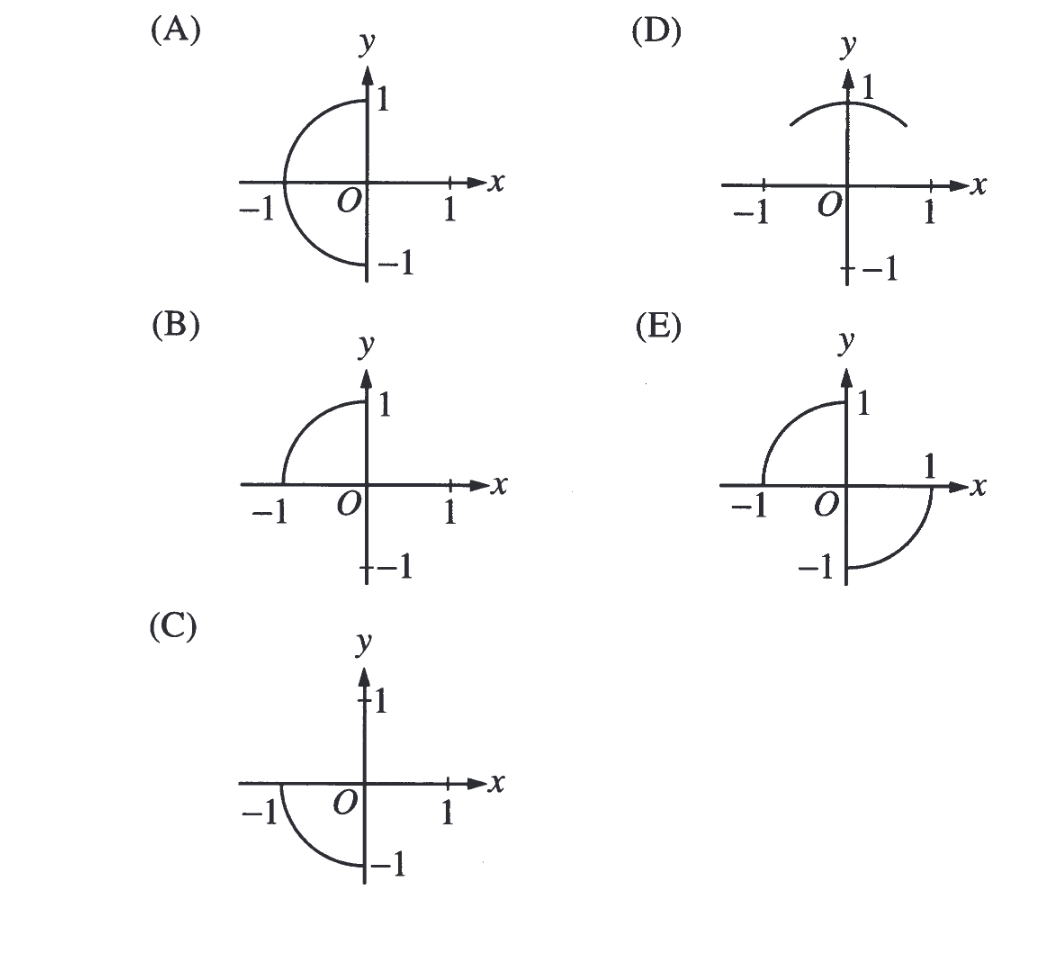
Какой из предложенных графиков изображает параметризованную функцию {(sin(t), cos(t)), где t <m>\in</m>  [<m>-\frac{\pi}{2}</m>; 0]}
−
Тут вставьте перевод вопроса.
+
−
Используйте [https://wiki.4intra.net/Help:%D0%A4%D0%BE%D1%80%D0%BC%D0%B0%D1%82%D0%B8%D1%80%D0%BE%D0%B2%D0%B0%D0%BD%D0%B8%D0%B5 возможности разметки],
+
−
включая формулы и т.п, если будут графы — посмотрите как задать их текстом https://wiki.4intra.net/Graphviz (реально оценю, полезный навык).
+
  
−
В IT вообще не принято писать романы, всегда старайтесь писать структурированные (списками-абзацами тексты). Списки в MediaWiki — это просто «*». Не забывайте о них.
+
[[Файл:Снимок экрана 2025-01-12 в 15.22.30.png]]
−
* Преформатированный моноширинный текст — просто отступ.  
+
−
* Короткая математика — тег <nowiki><m>\sum_i^100 i^2</m></nowiki>
+
−
* Большой LaTeX-блок (пример [[2008-gre-math-0568.pdf/Q09]])
+
−
<nowiki><latex>
+
−
… Lores ipsum $\sum_i^100 i^2$ …
+
−
</latex></nowiki>
+
−
 
+
−
Старайтесь нетривиальные понятия, особенно незнакомые вам, найти ссылку на википедию и вставить (нейросети лажают!).
+
−
Это важно, чтобы найти корректный перевод (то, что в википедии, или на худой конец — точно массово гуглится).
+
−
 
+
−
Потом конечно сотрите эти инструкции, которые тут курсивом или в блоке цитирования (и тег «blockquote»).
+
−
</blockquote>
+
  
 
=== Ответы ===
 
=== Ответы ===
−
<i>Если ответы простые, однострочные, используйте простой способ задания ответов списком, типа так
 
−
(префикс «Правильный ответ:» — это дословно, для правильного ответа, неважно, какой он будет в списке)</i>
 
  
−
* Правильный ответ: тут реально правильный ответ
+
* A
−
* неправильный ответ
+
* Правильный ответ: B
−
* еще какой-то неправильный ответ
+
* C
−
* еще какой-то неправильный ответ
+
* D
−
* еще какой-то неправильный ответ
+
* E
  
−
<i>Если ответы длинные, многострочные, или там графы, используйте
+
=== Объяснение ===
−
[https://wiki.4intra.net/MediawikiQuizzer/ru#.D0.9E.D1.82.D0.B2.D0.B5.D1.82.D1.8B способ задания ответов разделами],
+
{{cstest-source|2001-gre-math.pdf|16|7}}
−
Но такое очень редко встречается, например [[2011-gre-cs-practice-book.pdf/Q05]]. </i>
+
  
  
−
=== Объяснение ===
+
<code-python>
−
<i>Сначала заполните номер страницы с этим вопросом
+
from sympy import symbols, cos, sin, pi
−
{{cstest-source|2001-gre-math.pdf|тут-номер-страницы-с-вопросом-7|7}}
+
from sympy.plotting import plot_parametric
  
−
Если все сделаете правильно, по ссылке выше будет открываться правильная страница в правильном PDFе.
+
t = symbols('t')
 +
x = sin(t)
 +
y = cos(t)
  
−
Ну и наконец, вики-разметкой напишите ваше понимание, почему правильный ответ — правильный, а неправильные варианты — неправильны.
+
plot_parametric(x, y, (t, -0.5 * pi, 0), title='График из условия', xlabel='x(t)', ylabel='y(t)')
−
Конкретно здесь, в математических тестах ожидается в большинстве случаев просто блок питон-кода с использованием sympy,
+
# Выведет график как во варианте B.
−
см. [[Blog:Advanced_Algorithms/Потренируйтесь_в_sympy_на_детских_тестах_по_математике]], просто добавьте ваш код в этот тег:
+
−
 
+
−
<code-python>
+
−
from sympy import *
+
−
....
+
 
</code-python>
 
</code-python>
  
−
Но если уж sympy неприменим, распишите плиз, как понимаете 🤷‍♂️.
 
−
</i>
 
  
 
{{reserve-task|[[Участник:KoshelevEA|KoshelevEA]] 06:00, 8 января 2025 (UTC)}}
 
{{reserve-task|[[Участник:KoshelevEA|KoshelevEA]] 06:00, 8 января 2025 (UTC)}}
 +
{{checkme|[[Участник:KoshelevEA|KoshelevEA]] 12:32, 12 января 2025 (UTC)}}
 
{{question-ok|}}
 
{{question-ok|}}
  
 
[[Категория:Математика]]
 
[[Категория:Математика]]

Версия 12:32, 12 января 2025

Вопрос: Q07-19def7

Какой из предложенных графиков изображает параметризованную функцию {(sin(t), cos(t)), где t [; 0]}

Снимок экрана 2025-01-12 в 15.22.30.png

Ответы

  • A
  • Правильный ответ: B
  • C
  • D
  • E

Объяснение

Исходники — вопрос 7 на 16 странице книги «2001-gre-math.pdf» 


from sympy import symbols, cos, sin, pi
from sympy.plotting import plot_parametric
 
t = symbols('t')
x = sin(t)
y = cos(t)
 
plot_parametric(x, y, (t, -0.5 * pi, 0), title='График из условия', xlabel='x(t)', ylabel='y(t)')
# Выведет график как во варианте B.

Задача зарезервирована: KoshelevEA 06:00, 8 января 2025 (UTC)

Check-me-animated.gif Решено: KoshelevEA 12:32, 12 января 2025 (UTC)

Источник — «https://discopal.ispras.ru/index.php?title=2001-gre-math.pdf/Q07&oldid=35694»