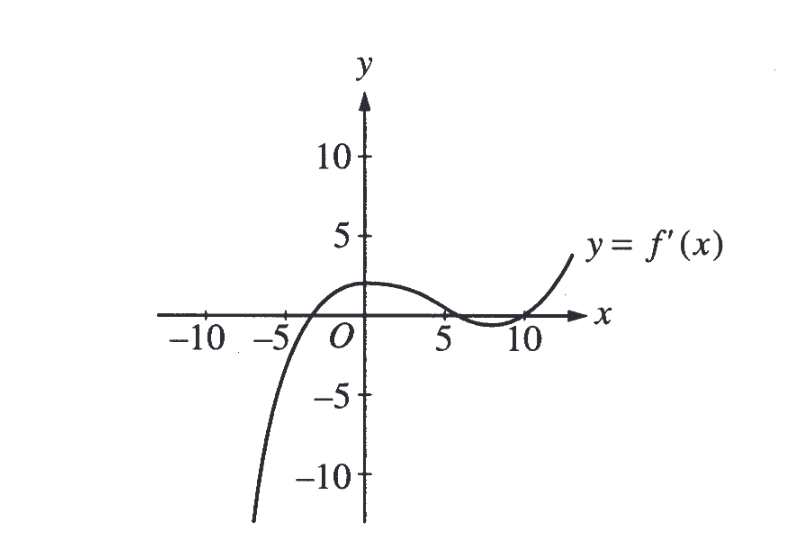2001-gre-math.pdf/Q05 — различия между версиями
StasFomin (обсуждение | вклад) |
(→Вопрос: Q05-19def7) |
||
| Строка 24: | Строка 24: | ||
Ответ, график E. | Ответ, график E. | ||
| − | + | {{reserve-task|[[Участник:KoshelevEA|KoshelevEA]] 21:17, 12 января 2025 (UTC)}} | |
{{BadSol}} Нет, так не пойдет. Надо чтобы варианты были каждый отдельно, отдельным элементом списка, или разделом. Ну не беритесь за такие, сейчас уже нет времени обьяснять, если вы не смотрели как оформлять. | {{BadSol}} Нет, так не пойдет. Надо чтобы варианты были каждый отдельно, отдельным элементом списка, или разделом. Ну не беритесь за такие, сейчас уже нет времени обьяснять, если вы не смотрели как оформлять. | ||
Версия 21:17, 12 января 2025
Вопрос: Q05-19def7
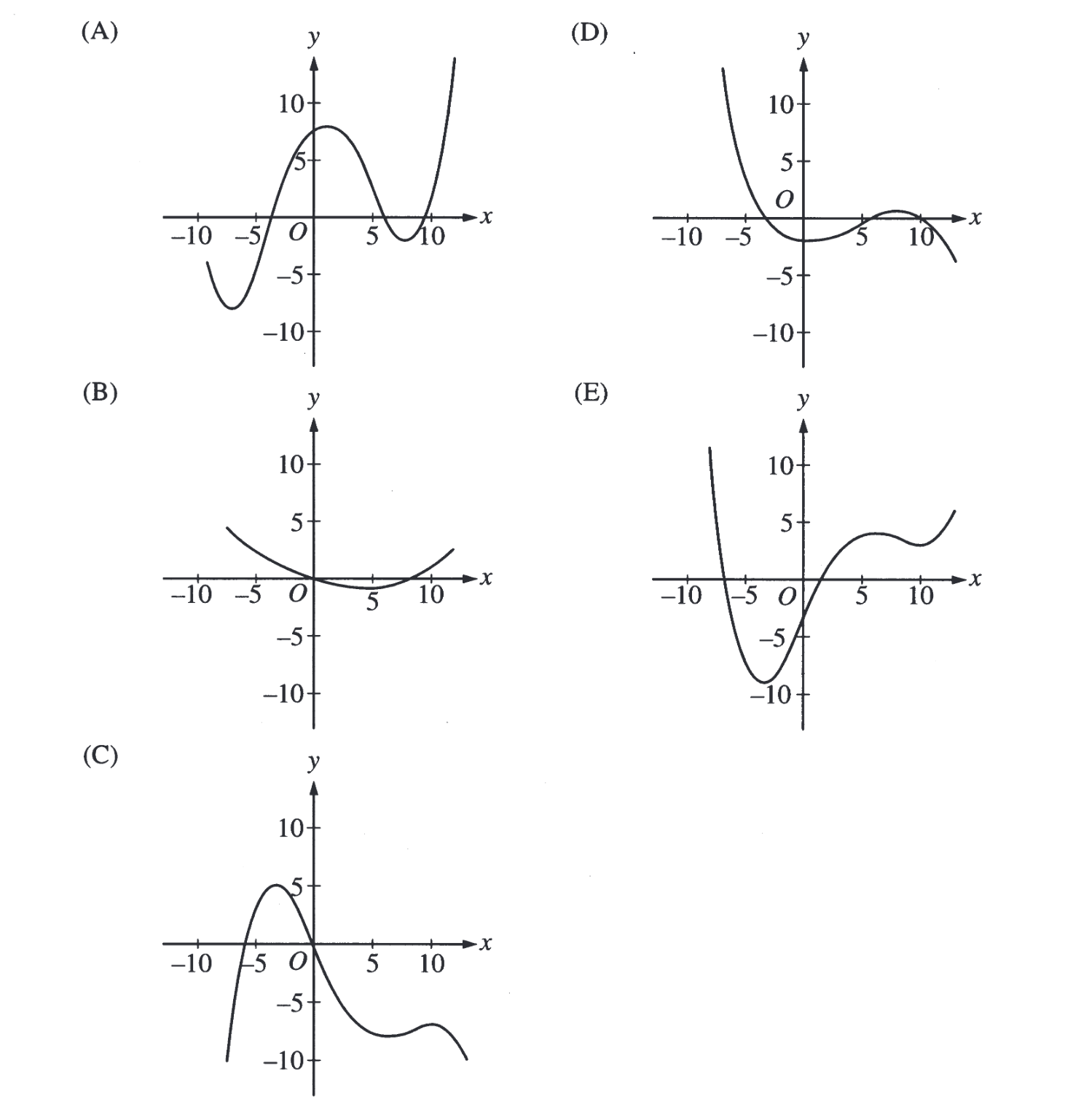
На предложенном графике изображена производная некоторой функции y = f'(x). Как может выглядеть сама функция f(x)?
Ответы
- A
- B
- C
- D
- Правильный ответ: E
Объяснение
Исходники — вопрос 5 на 14 странице книги «2001-gre-math.pdf»
График производной функции пересекает прямую y=0 в точке между -5 и 0. Назовем эту точку A, т.к. производная в этой точке зануляется, то график самой функции в этой точке должен иметь экстремум. Из предложенных, этому удовлетворяют только графики C и E. Далее, в точке -5 производная < 0, а значит функция должна убывать в этой точке. Этому удовлетворяет только график E. Ответ, график E.
Задача зарезервирована: KoshelevEA 21:17, 12 января 2025 (UTC)
Шаблон:BadSol Нет, так не пойдет. Надо чтобы варианты были каждый отдельно, отдельным элементом списка, или разделом. Ну не беритесь за такие, сейчас уже нет времени обьяснять, если вы не смотрели как оформлять.