Графы-расширители — различия между версиями
Материал из DISCOPAL
StasFomin (обсуждение | вклад) |
StasFomin (обсуждение | вклад) |
||
| Строка 8: | Строка 8: | ||
* [https://ru.wikibrief.org/wiki/Expander_graph Расширительный граф на вики-бриф] | * [https://ru.wikibrief.org/wiki/Expander_graph Расширительный граф на вики-бриф] | ||
* [https://nplus1.ru/material/2020/04/06/abel Расширьтесь, граф] | * [https://nplus1.ru/material/2020/04/06/abel Расширьтесь, граф] | ||
| − | |||
| − | |||
| − | |||
=== Разрез / Edge-CUT . === | === Разрез / Edge-CUT . === | ||
[[File:edge-cut-01.png|center]] | [[File:edge-cut-01.png|center]] | ||
| + | * См. [[MAX-CUT]] | ||
=== «Относительная трудноразрезаемость» . === | === «Относительная трудноразрезаемость» . === | ||
| Строка 20: | Строка 18: | ||
[[File:edge-cut-01.png|256px|right]] | [[File:edge-cut-01.png|256px|right]] | ||
| − | * <m>|\partial S|=8</m> | + | * «Сложно разрезать при минимуме ребер» |
| + | ** Это «экспандеры/расширители» | ||
| + | |||
| + | === Термины . === | ||
| + | |||
| + | [[File:edge-cut-01.png|256px|right]] | ||
| + | |||
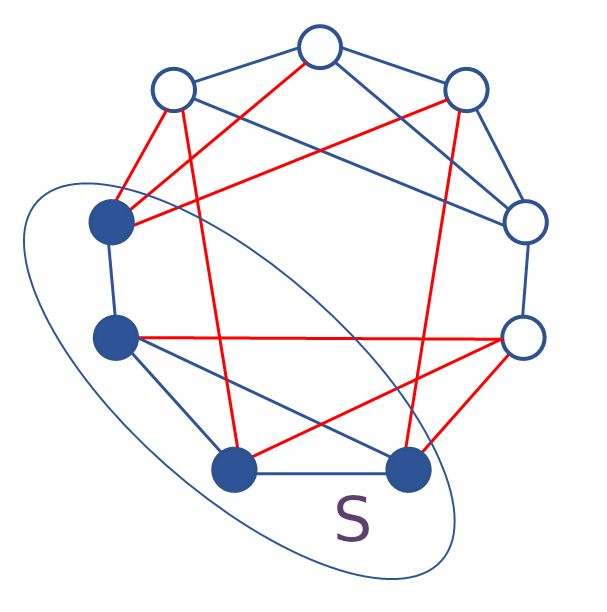
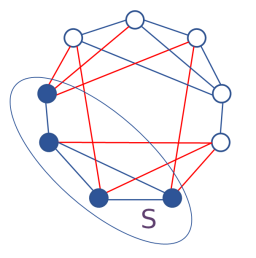
| + | Для подмножества ''S'' вершин ''G'', | ||
| + | * {{!|граница/boundary}} ''S'' → <m>\partial S</m> | ||
| + | ** тут <m>|\partial S|=8</m> | ||
| + | |||
| + | <m>h(G)=\min_{S,0<|S|\leq n/2}|\partial S|/|S|</m> — «константа реберного расширения» (Cheeger) | ||
| + | |||
| + | * Ищем такие графы ''G'', чтобы был минимум ребере при большой <m>h(G)</m> | ||
Версия 08:36, 16 апреля 2024
- Заголовок
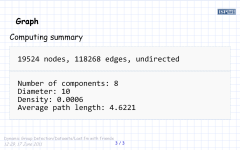
- Графы-расширители
- Автор
- Стас Фомин
- Нижний колонтитул
- Графы-расширители
- Дополнительный нижний колонтитул
- Стас Фомин, 09:39, 16 апреля 2024
Источники .
- Книги
- Графы-расширители и их применения в теории кодирования,
- Экспандеры: конструкции и приложения
- Расширительный граф на вики-бриф
- Расширьтесь, граф
Разрез / Edge-CUT .
- См. MAX-CUT
«Относительная трудноразрезаемость» .
- «Сложно разрезать при минимуме ребер»
- Это «экспандеры/расширители»
Термины .
Для подмножества S вершин G,
- граница/boundary S →
- тут
— «константа реберного расширения» (Cheeger)
- Ищем такие графы G, чтобы был минимум ребере при большой