2001-gre-math.pdf/Q05 — различия между версиями
Материал из DISCOPAL
(→Вопрос: Q05-19def7) |
StasFomin (обсуждение | вклад) |
||
| Строка 3: | Строка 3: | ||
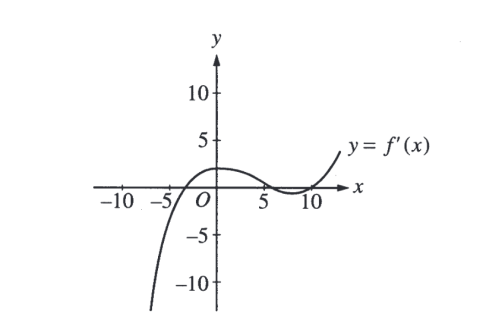
На предложенном графике изображена производная некоторой функции y = f'(x). Как может выглядеть сама функция f(x)? | На предложенном графике изображена производная некоторой функции y = f'(x). Как может выглядеть сама функция f(x)? | ||
| − | [[Файл:Graph derivative.png]] | + | [[Файл:Graph derivative.png|480px]] |
| − | ==== Ответ ==== | + | ==== Ответ ==== |
| − | [[Файл:a_graph.png]] | + | [[Файл:a_graph.png|256px]] |
| − | ==== Ответ ==== | + | ==== Ответ ==== |
| − | [[Файл:b_graph.png]] | + | [[Файл:b_graph.png|256px]] |
| − | ==== Ответ ==== | + | ==== Ответ ==== |
| − | [[Файл:c_graph.png]] | + | [[Файл:c_graph.png|256px]] |
| − | ==== Ответ ==== | + | ==== Ответ ==== |
| − | [[Файл:d_graph.png]] | + | [[Файл:d_graph.png|256px]] |
| − | ==== Правильный ответ ==== | + | ==== Правильный ответ ==== |
| − | [[Файл:e_graph.png]] | + | [[Файл:e_graph.png|256px]] |
=== Объяснение === | === Объяснение === | ||
{{cstest-source|2001-gre-math.pdf|14|5}} | {{cstest-source|2001-gre-math.pdf|14|5}} | ||
| − | График производной функции пересекает прямую y=0 в точке между | + | График производной функции пересекает прямую y=0 в точке между −5 и 0. Назовем эту точку A, так как производная в этой точке зануляется, то график самой функции в этой точке должен иметь экстремум. |
Из предложенных, этому удовлетворяют только графики C и E. | Из предложенных, этому удовлетворяют только графики C и E. | ||
| − | Далее, в точке | + | |
| + | Далее, в точке −5 производная < 0, а значит функция должна убывать в этой точке. Этому удовлетворяет только график E. | ||
Ответ, график E. | Ответ, график E. | ||
| − | {{ | + | {{question-ok|[[Участник:StasFomin|StasFomin]] 11:06, 13 января 2025 (UTC)}} |
| − | + | ||
| − | + | ||
| − | + | ||
[[Категория:Математика]] | [[Категория:Математика]] | ||
Текущая версия на 11:06, 13 января 2025
Содержание
Вопрос: Q05-19def7
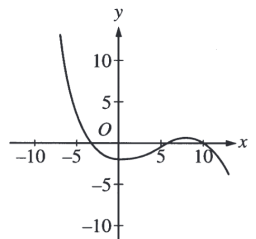
На предложенном графике изображена производная некоторой функции y = f'(x). Как может выглядеть сама функция f(x)?
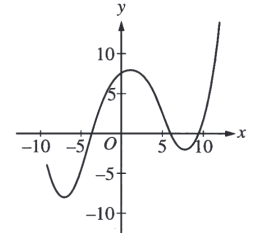
Ответ
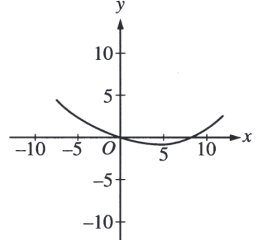
Ответ
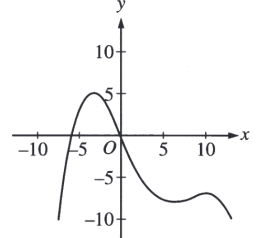
Ответ
Ответ
Правильный ответ
Объяснение
Исходники — вопрос 5 на 14 странице книги «2001-gre-math.pdf»
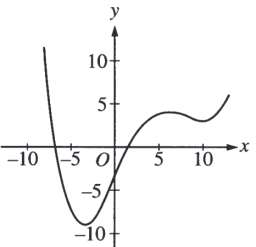
График производной функции пересекает прямую y=0 в точке между −5 и 0. Назовем эту точку A, так как производная в этой точке зануляется, то график самой функции в этой точке должен иметь экстремум. Из предложенных, этому удовлетворяют только графики C и E.
Далее, в точке −5 производная < 0, а значит функция должна убывать в этой точке. Этому удовлетворяет только график E. Ответ, график E.