Open Exercises

Материал из DISCOPAL
Версия от 09:29, 19 апреля 2023; StasFomin (обсуждение | вклад) (Копия ревизии 25388 статьи Open Classic Hard Problems)

(разн.) ← Предыдущая | Текущая версия (разн.) | Следующая → (разн.)
Перейти к: навигация, поиск

Всего страниц найдено: 208.

Задача «Minimum Metric Traveling Salesperson Problem»©

  • Набор C из m городов с заданными расстояниями между ними для каждой пары городов. Расстояния удовлетворяют неравенству треугольника!
  • Найти тур C, т.е. перестановка .
  • Минимизировать длину этого тура

Код в «minimum-metric-traveling-salesperson-problem.ipynb» на гитлаб или живьем в лабе

Задача «Maximum D-Vector Covering»©

  • Набор X векторов из .
  • Найти разбиение X на m подмножеств
  • Максимизировать покрывающих подмножеств среди , где «покрывающим» подмножество S векторов из , считается, если для всех i ≤ d сумма i-х компонент элементов из S будет не меньше 1.

Код в «maximum-d-vector-covering.ipynb» на гитлаб или живьем в лабе

Задача «Minimum Local Register Allocation»©

  • Набор инструкций, формирующих некий блок без переходов,
    • N доступных регистров,
    • стоимость чтения и записи в регистр i.
  • Порядок резервирования регистров для этой последовательности инструкций.
  • Минимизировать полную стоимость чтения-записи в регистры.

Код в «minimum-local-register-allocation.ipynb» на гитлаб или живьем в лабе

Задача «Minimum Multiprocessor Scheduling»©

  • Набор задач T, m процессоров, время выполнения .
  • Найти m-процессорное расписание для T, т.е. функцию .
  • Минимизировать время выполнения расписания, т.е.

Код в «minimum-multiprocessor-scheduling.ipynb» на гитлаб или

Задача «Minimum Graph Coloring»©

Граф G=(V,E).

Найти раскраску G, т.е. разбиение V на непересекающиеся наборы

V1, V2, …, Vk, такие, что каждый Vi независимое множество в G.

Минимизировать размерность раскраски, т.е. число этих независимых наборов Vi.

Код в «minimum-graph-coloring.ipynb» на гитлаб или живьем в лабе

Задача «Maximum Knapsack»©

Maximum-knapsack.png
  • Конечное множество U, для каждого u ∈ U задан
    • вес-размер
    • ценность
  • Положительное целое — размер рюкзака.
  • Выбрать подмножество U' ⊆ U, не превышающее емкость рюкзака:
  • Максимизировать ценность выбранных элементов, .


Код в «maximum-knapsack.ipynb» на гитлаб или живьем в лабе

  • Data-vis-logo.png — есть тестовые данные и визуализация.
  • PyomoLogo.png — есть Pyomo-формулировка для ЦЛП.

Временно желательно не брать — там сложный случай, работаем, чтобы заставить ЦЛП-солвер решать постановку.

Задача «Minimum Test Collection»©

  • Коллекция C подмножеств конечного множества S.
  • Найти подколлекцию C'⊆ C, такую, что для каждой пары различных элементов (и для каждого элемента этой пары) , есть некоторое подмножество , которое содержит точно один элемент из этой пары.
  • Минимизировать мощность этой подколлекции |C'|.

Для понимания названия задачи, представим, что S — это множество возможных болезней, а подмножества — это симптомы (или «тесты»), которые могут быть характерны для нескольких болезней. И мы должны выбрать такой набор симптомов-тестов, чтобы имея результаты, мы могли отличить у пациента любые пары болезней.

Код в «minimum-test-collection.ipynb» на гитлаб или

Задача «Maximum Clique»©

  • Граф G=(V,E).
  • Найти клику в G, т.е. подмножество вершин V'⊆V, такое что любая пара вершин в V' соединены ребром из E.
  • Максимизировать размер клики, т.е. |V'|.

Код в «maximum-clique.ipynb» на гитлаб или живьем в лабе

Задача «Minimum Sum Of Squares»©

  • Конечное множество A, задан размер для каждого a ∈ A, и целое K ≥ 2 .
  • Найти разбиение A на множество из K непересекающихся множеств A1, A2, …, AK.
  • Минимизировать сумму квадратов их размеров

Код в «minimum-sum-of-squares.ipynb» на гитлаб или живьем в лабе

Задача «Minimum 3-Dimensional Assignment»©

  • Три множества X, Y, W и функция стоимости c: X×Y×W → N
  • Найти назначение A, т.е. подмножество A ⊆ X×Y×W, такой что каждый элемент из принадлежит только одной тройке из A.
  • Минимизировать стоимость назначения, т.е.

Код в «minimum-3-dimensional-assignment.ipynb» на гитлаб или

Задача «Minimum K-Satisfiability»©

  • Константа k≥2, множество переменных U,
  • Коллекция C скобок-дизъюнкций литералов, где литерал это какая-то переменная или ее отрицание, размер скобки не больше k.
  • Найти истинное присваивание для U.
  • Минимизировать число выполненных скобок.

Код в «minimum-k-satisfiability.ipynb» на гитлаб или

Задача «Maximum Cut»©

Maximum-cut.png
  • Граф G=(V,E).
  • Найти разбиение V на непересекающиеся множества V1 и V2.
  • Максимизировать размер разреза, т.е. число ребер, в которых один конец в множестве V1, а другой конец в V2.

Код в «maximum-cut.ipynb» на гитлаб или Data-vis-logo.png — есть тестовые данные и визуализация.

  • PyomoLogo.png — есть Pyomo-формулировка для ЦЛП. '>📺 видео 📺819175567Задача в базе NP-полных задач Вигго Кана
  • Код задачи в книге «ГД» → «ND16»

    • Задача «Maximum Set Splitting»©

    Maximum-set-splitting.svg
    • Коллекция C подмножеств конечного множества S.
    • Найти разбиение S, на непересекающиеся множества S1 и S2.
    • Максимизировать число подмножеств C, которые «разделены» между S1 и S2, т.е. не лежат полностью в S1 или S2.

    Код в «maximum-set-splitting.ipynb» на гитлаб или Data-vis-logo.png — есть тестовые данные и визуализация.

  • PyomoLogo.png — есть Pyomo-формулировка для ЦЛП. '>📺 видео 📺819542576📺 видео 📺820790843'>📺 видео 📺
  • Yes-you-can-icon.png Можно доработать — сделать Вероятностное тестирование NPC-сведения!

    • Задача «Minimum Exact Cover»©

    Minimum-exact-cover.svg
    • Коллекция C подмножеств конечного множества S.
    • Найти покрытие множества S, на т.е. подмножество C'⊆ C, такое, что для каждый элемент из S принадлежит по крайней мере одному подмножеству из C'.
    • Минимизировать суммарных объем покрывающих подмножеств, т.е.

    Код в «minimum-exact-cover.ipynb» на гитлаб или Data-vis-logo.png — есть тестовые данные и визуализация.

  • PyomoLogo.png — есть Pyomo-формулировка для ЦЛП. '>📺 видео 📺819518997📺 видео 📺828547057Yes-you-can-icon.png Можно доработать — сделать Вероятностное тестирование NPC-сведения!

    • Задача «Maximum K-Satisfiability»©

    • Константа k≥2, множество переменных U,
    • Коллекция C скобок-дизъюнкций литералов, где литерал это какая-то переменная или ее отрицание, размер скобки не больше k.
    • Найти истинное присваивание для U.
    • Максимизировать число выполненных скобок.

    Код в «maximum-k-satisfiability.ipynb» на гитлаб или живьем в лабе

    • Data-vis-logo.png — есть тестовые данные и визуализация.
    • PyomoLogo.png — есть Pyomo-формулировка для ЦЛП.
    • Npc-reduction-python-logo.png — есть сведение на Python NP-полной задачи к данной.

    Задача «Minimum Traveling Salesperson»©

    • Набор C из m городов с заданными расстояниями между ними для каждой пары городов.
    • Найти тур C, т.е. перестановка .
    • Минимизировать длину этого тура

    Код в «minimum-traveling-salesperson.ipynb» на гитлаб или живьем в лабе

    Задача «Maximum Class-Constrained Knapsack»©

    • n размеров заданных вектором , m рюкзаков разных размеров и числом отсеков заданных векторами , причем .
    • Найти размещение заданных элементов в эти рюкзаки, заданный двумя n×m матрицами,

    , такой, что

    • Максимизировать число упакованных элементов 
    .


    Код в «maximum-class-constrained-knapsack.ipynb» на гитлаб или живьем в лабе

    Задача «Maximum Integer K-Choice Knapsack»©

    • Неотрицательные целочисленные m×k матрицы , неотрицательное целое b∈ N.
    • Найти
      • неотрицательный целочисленный n-вектор ,
      • функция
      • такие, что .
    • Максимизировать 
    .

    Код в «maximum-integer-k-choice-knapsack.ipynb» на гитлаб или живьем в лабе

    • Data-vis-logo.png — есть тестовые данные и визуализация.
    • PyomoLogo.png — есть Pyomo-формулировка для ЦЛП.

    Задача «Maximum Integer M-Dimensional Knapsack»©

    • Неотрицательная целочисленная m×n матрица
      • неотрицательный целочисленный вектор m-вектор .
    • Найти неотрицательный целочисленный n-вектор , такой что Ax≤b.
    • Максимизировать скалярное произведение c и x, т.е., .


    Код в «maximum-integer-m-dimensional-knapsack.ipynb» на гитлаб или живьем в лабе

    • Data-vis-logo.png — есть тестовые данные и визуализация.
    • PyomoLogo.png — есть Pyomo-формулировка для ЦЛП.

    Задача «Maximum Quadratic Programming»©

    Maximum-quadratic-programming.png
    • Положительное целое n, набор линейных ограничений заданных в виде m×n матрицы, и m-вектора b, задающие область ограничениями .
    • многомерный многочлен f, максимальной степени не больше 2. Имея
      • Q — симметричная положительно-полуопределенная матрица,
      • c — вектор линейных коэффициентов
    • Можно представить его в виде:
    • Максимизировать значение f в области заданной линейными ограничениями, т.е. .

    Код в «maximum-quadratic-programming.ipynb» на гитлаб или Data-vis-logo.png — есть тестовые данные и визуализация.

  • PyomoLogo.png — есть Pyomo-формулировка для ЦЛП. '>📺 видео 📺822121003'>📺 видео 📺

    • Задача «Maximum Bounded 0-1 Programming»©

    Maximum-bounded-0-1-programming.png
    • Целая m×n-матрица , целый m-вектор , неотрицательный бинарный -вектор .
    • Найти двоичный n-вектор , такой что Ax ≤ b.
    • Максимизировать скалярное произведение c и x, т.е., .

    Код в «maximum-bounded-0-1-programming.ipynb» на гитлаб или живьем в лабе

    • Data-vis-logo.png — есть тестовые данные и визуализация.
    • PyomoLogo.png — есть Pyomo-формулировка для ЦЛП.

    Задача «Minimum Covering Integer Programming»©

    Minimum-covering-integer-programming.png
    • Рациональная m×n-матрица , рациональный m-вектор , рациональный -вектор .
    • Найти рациональный n-вектор , такой что Ax≥b.
    • Минимизировать скалярное произведение c и x, т.е., .

    Код в «minimum-covering-integer-programming.ipynb» на гитлаб или живьем в лабе

    • Data-vis-logo.png — есть тестовые данные и визуализация.
    • PyomoLogo.png — есть Pyomo-формулировка для ЦЛП.

    Задача «Minimum 0-1 Programming»©

    Minimum-0-1-programming.png
    • Целая m×n-матрица , целый m-вектор , неотрицательный целый -вектор .
    • Найти двоичный n-вектор , такой что Ax≥b.
    • Минимизировать скалярное произведение c и x, т.е., .

    Код в «minimum-0-1-programming.ipynb» на гитлаб или живьем в лабе

    • Data-vis-logo.png — есть тестовые данные и визуализация.
    • PyomoLogo.png — есть Pyomo-формулировка для ЦЛП.

    Задача «Maximum Packing Integer Programming»©

    Maximum-packing-integer-programming.png
    • Рациональная m×n-матрица , рациональный m-вектор , рациональный -вектор .
    • Найти рациональный n-вектор , такой что Ax≤b.
    • Максимизировать скалярное произведение c и x, т.е., .

    Код в «maximum-packing-integer-programming.ipynb» на гитлаб или живьем в лабе

    • Data-vis-logo.png — есть тестовые данные и визуализация.
    • PyomoLogo.png — есть Pyomo-формулировка для ЦЛП.

    Задача «Minimum Upgrading Spanning Tree»©

    • Граф G=(V,E), три функции весов на ребрах (для всех e ∈ E), где означает вес ребра e, если i его концов «обновлены», причем известна стоимость обновления c(v) для каждой вершины v ∈ V, и некое ограничивающее значение D для веса минимального остовного дерева.
    • Найти набор обновляемых вершин W⊆V, так чтобы вес минимального остовного дерева с весами dW, была ограничена D.
      • dW означает вес ребра в результате обновления вершин в W, т.е. , где .
    • Минимизировать стоимость обновления вершин, т.е. .

    Код в «minimum-upgrading-spanning-tree.ipynb» на гитлаб или

    Задача «Maximum Set Packing»©

    Maximum-set-packing.svg
    • Коллекция конечных множеств C.
    • Найти упаковку множеств, т.е. коллекцию непересекающихся множество C'⊆ C.
    • Максимизировать размер этой упаковки, т.е. |C'|

    Код в «maximum-set-packing.ipynb» на гитлаб или Data-vis-logo.png — есть тестовые данные и визуализация.

  • PyomoLogo.png — есть Pyomo-формулировка для ЦЛП. '>📺 видео 📺819474091📺 видео 📺820661279Yes-you-can-icon.png Можно доработать — сделать Вероятностное тестирование NPC-сведения!

    • Задача «Maximum 3-Dimensional Matching»©

    Maximum-3-dimensional-matching.svg
    • Множество T ⊆ X×Y×Z, с непересекающимися X, Y, и Z.
    • Найти трехмерное сопоставление для T, т.е. подмножество M⊆T, такое, что его элементы не пересекаются ни по одной координате.
    • Максимизировать размер сопоставления, т.е. |M| → max.

    Код в «maximum-3-dimensional-matching.ipynb» на гитлаб или Data-vis-logo.png — есть тестовые данные и визуализация.

  • PyomoLogo.png — есть Pyomo-формулировка для ЦЛП. '>📺 видео 📺819576517📺 видео 📺820657456Yes-you-can-icon.png Можно доработать — сделать Вероятностное тестирование NPC-сведения!

    • Задача «Minimum Set Cover»©

    Minimum-set-cover.svg
    • Коллекция C подмножеств конечного множества S.
    • Найти покрытие множества S, на т.е. подмножество C'⊆ C, такое, что для каждый элемент из S принадлежит по крайней мере одному подмножеству из C'.
    • Минимизировать число покрывающих подмножеств, т.е. |C'|→min.

    Код в «minimum-set-cover.ipynb» на гитлаб или Data-vis-logo.png — есть тестовые данные и визуализация.

  • PyomoLogo.png — есть Pyomo-формулировка для ЦЛП. '>📺 видео 📺819442881📺 видео 📺819623515Yes-you-can-icon.png Можно доработать — сделать Вероятностное тестирование NPC-сведения!

    • Задача «Minimum General Routing»©

    • Граф G=(V,E), длина l(e)∈ N на ребрах e ∈ E, подмножества E' ⊆ E, V'⊆V.
    • Цикл в G, который заходит ровно раз в каждую вершину из V' и пересекает каждое ребро из E'.
    • Минимизировать общую длину этого цикла.

    Код в «minimum-general-routing.ipynb» на гитлаб или живьем в лабе

    Задача «Minimum Preemptive Scheduling With Set-Up Times»©

    • Набор компиляторов C, набор задач T, m процессоров, длительности задач , нужный для задачи компилятор , время запуска-настройки для каждого компилятора .
    • Найти m-процессорное вытесняющее расписание T, т.е. для каждой для каждой задачи t ∈ T, разбиение t на какое-то количество подзадач t1, …, tk, такое что
      • и есть некоторое назначение , которое назначает каждой подзадаче ti пару неотрицательных целых , таких, что
      • Это расписание должно удовлетворять дополнительному ограничению:
        • Если два подзадачи ti от t и tj' от t', у которых запланированы последовательно на одном процессоре (т.е. , и нет другой подзадачи , у которой и , то
          • — если у них один и тот же компилятор (c(t) = c(t'))
          • — если эти компиляторы разные.
    • Минимизировать общее время выполнения, т.е. максимум по всем подзадачам

    Код в «minimum-preemptive-scheduling-with-set-up-times.ipynb» на гитлаб или живьем в лабе

    Задача «Minimum Cut Cover»©

    Minimum-cut-cover.png

    Граф G=(V,E).

    Найти коллекцию разрезов V1, …, Vm,

    т.е. коллекция подмножеств вершин , такая что каждое ребро графа (u,v)∈ E свои концы держит в разных подмножествах, т.е.

    • либо и
    • либо и

    Минимизировать размер «m» этой коллекции.

    Код в «minimum-cut-cover.ipynb» на гитлаб или Data-vis-logo.png — есть тестовые данные и визуализация.

  • PyomoLogo.png — есть Pyomo-формулировка для ЦЛП. '>📺 видео 📺819428357'>📺 видео 📺

    • Задача «Minimum K-Cut»©

    Minimum-k-cut.png
    • Граф G=(V,E), веса на ребрах w: E → N, целое .
    • Найти разбиение V на k непересекающихся множеств .
    • Минимизировать сумму весов между ребрами, которые между этими множествами

    Код в «minimum-k-cut.ipynb» на гитлаб или Data-vis-logo.png — есть тестовые данные и визуализация.

  • PyomoLogo.png — есть Pyomo-формулировка для ЦЛП. '>📺 видео 📺819413641'>📺 видео 📺

    • Задача «Maximum K-Cut»©

    Maximum-k-cut.png
    • Граф G=(V,E), веса на ребрах w: E → N, целое .
    • Найти разбиение V на k непересекающихся множеств .
    • Максимизировать сумму весов между ребрами, которые между этими множествами

    Код в «maximum-k-cut.ipynb» на гитлаб или Data-vis-logo.png — есть тестовые данные и визуализация.

  • PyomoLogo.png — есть Pyomo-формулировка для ЦЛП. '>📺 видео 📺819207635Задача в базе NP-полных задач Вигго Кана

    • Задача «Maximum Directed Cut»©

    Maximum-directed-cut.png
    • Направленный граф G=(V,A).
    • Найти разбиение V на непересекающиеся множества V1 и V2.
    • Максимизировать размер разреза, т.е. число дуг, которые стартуют в V1, и заканчиваются в V2.

    Код в «maximum-directed-cut.ipynb» на гитлаб или Data-vis-logo.png — есть тестовые данные и визуализация.

  • PyomoLogo.png — есть Pyomo-формулировка для ЦЛП. '>📺 видео 📺819189350'>📺 видео 📺

    • Задача «Minimum B-Balanced Cut»©

    Minimum-b-balanced-cut.png
    • Граф G=(V,E), веса на вершинах w: V → N, стоимости на ребрах c: E → N, рациональное число b, .
    • Найти разрез C, т.е. подмножество вершин C⊆V, такой, что

    , где where w(V') означает сумму весов вершин в V'.

    • Минимизировать вес разреза, т.е. 
    ,

    где

    Код в «minimum-b-balanced-cut.ipynb» на гитлаб или Data-vis-logo.png — есть тестовые данные и визуализация.

  • PyomoLogo.png — есть Pyomo-формулировка для ЦЛП., '>📺 видео 📺819130590'>📺 видео 📺

    • Задача «Minimum Cut Linear Arrangement»©

    • Граф G=(V,E).
    • Найти линейное упорядочивание V, т.е. биективную функцию .
    • Минимизировать максимальное число ребер разреза в любой целой точке, т.е. .

    Код в «minimum-cut-linear-arrangement.ipynb» на гитлаб или живьем в лабе

    Задача «Minimum Vertex K-Cut»©

    • Граф G=(V,E), набор , выделенных специальных вершин, веса для остальных вершин w: V-S → N, целое k.
    • Найти вершинный k-разрез, т.е. подмножество вершин , такое, что их удаление из графа отключает каждую специальную вершину si от ti для всех 1 ≤ i ≤ k.
    • Минимизировать сумму весов вершин в этом разрезе .

    Код в «minimum-vertex-k-cut.ipynb» на гитлаб или

    Задача «Maximum Induced Subgraph With Property P»©

    • Граф G=(V,E) и некое свойство (предикат) P над подграфами.
      • Свойство наследуемое, т.е. каждый подграф G' будет удовлетворять P, если сам G' ему удовлетворял.
      • Свойство нетривиальное, т.е. оно истинно и ложно для бесконечного количества графов.
    • Найти подмножество вершин V'⊆V, такое, что подграф порожденный V' имеет свойство P.
    • Максимизировать размер этого подграфа |V'|.

    Код в «maximum-induced-subgraph-with-property-p.ipynb» на гитлаб или живьем в лабе

    Задача «Minimum Register Sufficiency»©

    • Направленный ациклический граф G=(V,A)
    • Найти вычисление на G, которое использует k регистров, т.е.
      • порядок v1, …, vn на вершинах V
      • последовательность S0, …, Sn подмножеств V, удовлетворяющих
        • S0 — пустое
        • Sn — содержит все вершины с нулевой входящей степенью в G
        • 1 ≤ i ≤ n, , , и содержит все вершины u, для которых
    • Минимизировать число регистров,т.е. k.

    Код в «minimum-register-sufficiency.ipynb» на гитлаб или живьем в лабе

    Задача «Maximum Triangle Packing»©

    • Граф G=(V,E).
    • Найти «упаковку треугольников» для G, т.е. набор V1, V2, …, Vk непересекающихся подмножеств V,
      • каждое из которых содержит ровно три вершины — , 1 ≤ i ≤ k
      • и все три ребра , , есть в E.
    • Максимизировать размерность этой упаковки треугольников, т.е. число этих непересекающихся подмножеств Vi.

    Код в «maximum-triangle-packing.ipynb» на гитлаб или живьем в лабе

    Задача «Maximum Edge Subgraph»©

    • Граф G=(V,E) с весами на ребрах w: E → N, положительное целое k.
    • Найти подмножество V'⊆V, заданного размера |V'|=k
    • Максимизировать общий вес ребер подграфа порожденного V',

    Код в «maximum-edge-subgraph.ipynb» на гитлаб или

    Задача «Maximum Domatic Partition»©

    • Граф G=(V,E).
    • Найти разбиение V на непересекающиеся наборы V1, V2, …, Vk такие, что каждый Vi доминирующее множество над G.
    • Максимизировать размерность разделения, т.е. число этих непересекающихся множеств вершин Vi.

    Код в «maximum-domatic-partition.ipynb» на гитлаб или

    Задача «Minimum K-Edge Connected Subgraph»©

    • Граф G=(V,E), константа k ≥ 2 .
    • Найти k-реберно-связный остовный подграф G'=(V,E'), т.е. остовный подграф, который нельзя сделать несвязным, удалив меньше чем k ребер.
    • Минимизировать размер остова , т.е. |E'|.

    Код в «minimum-k-edge-connected-subgraph.ipynb» на гитлаб или

    Задача «Minimum K-Vertex Connected Subgraph»©

    • Граф G=(V,E), константа k ≥ 2 .
    • Найти k-вершинно-связный остовный подграф G'=(V,E'), т.е. остовный подграф, который нельзя сделать несвязным, удалив меньше чем k вершин.
    • Минимизировать размер остова , т.е. |E'|.

    Код в «minimum-k-vertex-connected-subgraph.ipynb» на гитлаб или живьем в лабе

    Задача «Minimum Parallel Processor Total Flow Time»©

    • Набор задач T, m идентичных процессоров, каждая задача t ∈ T имеет время выпуска и длительность .
    • Найти m-процессорное расписание для T, удовлетворяющее ограничениям времени выпуска, т.е. функция f : T → N , такая что для всех u ≥ 0 и для любого процессора i, если S(u,i) это набор задач для которых и , то

    и для каждой задачи t, .

    • Минимизировать полное время расписания, т.е.


    Код в «minimum-parallel-processor-total-flow-time.ipynb» на гитлаб или живьем в лабе

    Задача «Minimum Weighted Completion Time Scheduling»©

    • Набор задач T, m идентичных процессоров, каждая задача t ∈ T имеет
      • время выпуска
      • длительность .
      • вес .
    • Найти m-процессорное расписание для T, удовлетворяющее ограничениям времени выпуска, т.е. функция f : T → N , такая что для всех u ≥ 0 и для любого процессора i, если S(u,i) это набор задач для которых и , то

    и для каждой задачи t, .

    • Минимизировать взешенную сумму времен выполнения, т.е.

    Код в «minimum-weighted-completion-time-scheduling.ipynb» на гитлаб или живьем в лабе

    Задача «Maximum Degree Bounded Connected Subgraph»©

    • Граф G=(V,E), вес на ребрах w : E → N и целое d ≥ 2
    • Найти подмножество ребер E' ⊆ E, такое что подграф G'=(V,E') связный и нет вершин степени большей d.

    Максимизировать полный вес этого подграфа,

    Код в «maximum-degree-bounded-connected-subgraph.ipynb» на гитлаб или живьем в лабе

    Задача «Maximum Common Subgraph»©

    • Графы G1=(V1,E1) и G2=(V2,E2).
    • Найти общий подграф, т.е. подмножества E1' ⊆ E1 и E2' ⊆ E2, такие, что два подграфа и изоморфны.
    • Максимизировать размер общего подграфа, т.е. |E'|.

    Код в «maximum-common-subgraph.ipynb» на гитлаб или живьем в лабе

    Задача «Maximum Common Induced Subgraph»©

    • Графы G1=(V1,E1) и G2=(V2,E2).
    • Найти общий порожденный подграф, т.е. подмножества V1' ⊆ V1 и V2' ⊆ V2, такие, что два подграфа G1', порожденный и G2', порожденный изоморфны.
    • Максимизировать размер общего подграфа, т.е. .

    Код в «maximum-common-induced-subgraph.ipynb» на гитлаб или

    Задача «Minimum Graph Transformation»©

    • Графы G1=(V1,E1) G2=(V2,E2).
    • Найти набор ребер E'⊆ E1, которых надо удалить из E1 и добавить в E2.
    • Минимизировать размер этого множества ребер, |E'|

    Код в «minimum-graph-transformation.ipynb» на гитлаб или живьем в лабе

    Задача «Minimum Separating Subdivision»©

    • Семейство непересекающихся полигонов P1, …, Pk.
    • Найти разделяющее подразделение, т.е. семейство из -полигонов R1, …, Rk, с попарно непересекающимися границами, такими, что для каждого , Pi ⊆ Ri.
    • Минимизировать размер подразделения, т.е. полное число ребер в полигонах R1, …, Rk.

    Код в «minimum-separating-subdivision.ipynb» на гитлаб или живьем в лабе

    Задача «Minimum Geometric Traveling Salesperson»©

    • Набор C ⊆ Z×Z из m точек на плоскости.
    • Тур C, т.е. перестановка .
    • Минимизировать длину тура где расстояние между точками (x1, y1) и (x2, y2) это округленная Евклидова длина

    Код в «minimum-geometric-traveling-salesperson.ipynb» на гитлаб или живьем в лабе

    Задача «Maximum Balanced Connected Partition»©

    Связный граф G=(V,E) с неотрицательными весами на вершинах w: V → N.

    Найти разбиение вершин V на непустые непересекающиеся множества (V1, V2), такие,

    что подграфы порожденные V1 и V2 являются связными.

    Минимизировать дисбаланс разбиения, т.е.

    , где

    Максимизировать размер этого разбиения.

    Код в «maximum-balanced-connected-partition.ipynb» на гитлаб или живьем в лабе

    Задача «Maximum Disjoint Connecting Paths»©

    • Мультиграф G=(V,E), коллекция пар вершин .
    • Найти коллекцию непересекающихся по ребрам путей в G соединающих некоторые из пар (si, ti), т.е. путь это последовательность вершин u1, u2, …, um, такая что для некоторого i, , и для всех j, .
    • Максимизация числа пар вершин (si, ti), которые будут соединены этими путями.

    Код в «maximum-disjoint-connecting-paths.ipynb» на гитлаб или живьем в лабе

    Задача «Maximum Integral K-Multicommodity Flow On Trees»©

    • Дерево T=(V,E), пропускная способность на ребрах c: E → N, k пар вершин (si, ti).
    • Найти поток , для каждой пары (si, ti), такой что , где , если e лежит на (единственном, тут дерево) пути из si в ti, и 0 в противном случае.
    • Максимизировать сумму потоков

    Код в «maximum-integral-k-multicommodity-flow-on-trees.ipynb» на гитлаб или

    Задача «Maximum Achromatic Number»©

    Граф G=(V,E).

    Найти полную раскраску G, т.е. разбиение V на непересекающиеся наборы V1, V2, …, Vk, такие, что каждый Vi

    • независимое множество в G,
    • для каждой пары этих непересекающихся множеств Vi, Vj, Vi ∪ Vj не является независимым множеством.

    Максимизировать размерность раскраски, т.е. число этих независимых наборов Vi.

    Код в «maximum-achromatic-number.ipynb» на гитлаб или живьем в лабе

    Задача «Minimum B-Vertex Separator»©

    • Граф G=(V,E), рациональное b, .
    • Найти разбиение V на непересекающиеся множества A, B, и C, такие что , и ни одно ребро не лежит разными концами в A и B одновременно.
    • Минимизировать размер разделителя, т.е. |C|.

    Код в «minimum-b-vertex-separator.ipynb» на гитлаб или живьем в лабе

    Задача «Shortest Common Supersequence»©

    • Конечный алфавит Σ, конечный набор R строк из .
    • Найти строку , такую что каждая строка x ∈ R является ее подпоследовательностью, т.е. можно получить x вычеркиванием символов из w.
    • Минимизировать длину этой суперпоследовательности |w|.

    Код в «shortest-common-supersequence.ipynb» на гитлаб или живьем в лабе

    Задача «Shortest Common Superstring»©

    • Конечный алфавит Σ, конечный набор R строк из .
    • Найти строку , такую что каждая строка x ∈ R является ее подстрокой, т.е. , для каких-то .
    • Минимизировать длину этой суперстроки |w|.

    Код в «shortest-common-superstring.ipynb» на гитлаб или

    Задача «Minimum Edge Coloring»©

    Граф G=(V,E).

    Найти полную раскраску ребер E, т.е. разбиение E на непересекающиеся наборы

    E1, E2, …, Ek, такие, что

    • никакие два ребра из Ei не имеют общей вершины из G.

    Минимизировать размерность раскраски, т.е. число этих независимых наборов Ei.

    Код в «minimum-edge-coloring.ipynb» на гитлаб или живьем в лабе

    Задача «Minimum K-Clustering»©

    • Конечное множество X, расстояние , для каждой пары, удовлетворяет неравенству треугольника.
    • Найти подразделение X на непересекающиеся подмножества C1, C2, …, Ck.
    • Минимизировать максимальное расстояние между элементами одного подмножества, т.е.

    Код в «minimum-k-clustering.ipynb» на гитлаб или живьем в лабе

    Задача «Minimum K-Clustering Sum»©

    • Конечное множество X, расстояние , для каждой пары, удовлетворяет неравенству треугольника.
    • Найти подразделение X на непересекающиеся подмножества C1, C2, …, Ck.
    • Минимизировать сумму всех расстояний между элементами одного подмножества, т.е.

    Код в «minimum-k-clustering-sum.ipynb» на гитлаб или живьем в лабе

    Задача «Minimum Maximum Disjoint Connecting Paths»©

    • Граф G=(V,E), пути на ребрах l: E → N, и некоторая пара вершин s,t в V. Найти два непересекающихся по вершинам пути в G, соединающих s и t, т.е. две последовательности вершин u1, u2, …, um и v1, v2, …, vn, такие что
    • Минимизировать максимальную длину этих путей, т.е.

    Код в «minimum-maximum-disjoint-connecting-paths.ipynb» на гитлаб или живьем в лабе

    Задача «Maximum H-Matching»©

    • Граф и фиксированный граф , с по крайней мере тремя вершинами в каком-нибудь связном компоненте.
    • Найти H-сочетание для G, т.е. коллекцию G1, G2, …, Gk, непересекающихся подграфов G, каждый из которых изоморфен H.
    • Максимизировать размерность H-сочетаний, т.е. число непересекающихся подграфов Gi.

    Код в «maximum-h-matching.ipynb» на гитлаб или живьем в лабе

    Задача «Minimum Bin Packing»©

    • Конечное множество элементов U, с заданными размерами , и емкость контейнера — положительное целое B.
    • Найти разбиение U на непересекающиеся множества U1, U2, …, Um, такие что сумма размеров элементов в каждом Ui не превышает B.
    • Минимизировать число используемых контейнеров, т.е. число непересекающихся множеств, m.

    Код в «minimum-bin-packing.ipynb» на гитлаб или

    Задача «Minimum Clique Cover»©

    • Граф G=(V,E).
    • Найти покрытие кликами для G, т.е. коллекция подмножеств вершин V1, V2, …, Vk, таких, что каждая порождает полный подграф, и каждое ребро (u,v) ∈ E содержит оба своих конца в одном из Vi.
    • Минимизировать размер «k» этого покрытия кликами.

    Код в «minimum-clique-cover.ipynb» на гитлаб или

    Задача «Minimum Clique Partition»©

    • Граф G=(V,E).
    • Найти разбиение на клики G, т.е. разбиение вершин V на непересекающиеся подмножества V1, V2, …, Vk, такие что для всех 1≤i≤k, подграф, порожденный вершинами из Vi будет полным графом.
    • Максимизировать размер этого разбиения.

    Код в «minimum-clique-partition.ipynb» на гитлаб или живьем в лабе

    Задача «Minimum Color Sum»©

    • Граф G=(V,E).
    • Найти раскраску G, т.е. разбиение V на непересекающиеся наборы V1, V2, …, Vk, такие, что каждый Vi независимое множество в G.
    • Минимизировать «сумму раскрасок», т.е. .

    Код в «minimum-color-sum.ipynb» на гитлаб или живьем в лабе

    Задача «Longest Path»©

    • Граф G=(V,E).
    • Найти простой путь в G, т.е. набор различных вершин v1, v2, …, vm, такой что .
    • Минимизировать длину пути, т.е. число ребер в этом пути.

    Код в «longest-path.ipynb» на гитлаб или живьем в лабе

    Задача «Minimum K-Capacitated Tree Partition»©

    • Граф G=(V,E) с весами w: E → N.
    • Найти k-мощное разбиение G на деревья, т.е. непересекающаяся коллекция подмножеств E1, …, Em ребер из E, так, что подграф порожденный каждым Ei будет давать дерево, минимум из k вершин.
    • Минимизировать вес этого разбиения: .

    Код в «minimum-k-capacitated-tree-partition.ipynb» на гитлаб или живьем в лабе

    Задача «Minimum Unsplittable Flow»©

    • Граф G=(V,E), емкости на ребрах , вершина-источник s, коллекция вершин-стоков t1, …, tk, с привязанными неотрицательными целочисленными запросами , такое, что .
    • Найти для каждого типа i единый путь , такой что все запросы удовлетворены, и полный поток проходящий через любое ребро e ограничено c(e).
    • Минимизировать , где f(e) это полный поток проходящий через e.

    Код в «minimum-unsplittable-flow.ipynb» на гитлаб или живьем в лабе

    Задача «Maximum Independent Sequence»©

    • Граф G=(V,E).
    • Найти независимую последовательность в G, т.е. последовательность независимых вершин, v1, …, vm, таких, что для любого i < m, если вершина соседствует с , но то оно не будет соседствовать ни с одним vj для любого j ≤ i.
    • Максимизировать «m» — длину этой последовательности.

    Код в «maximum-independent-sequence.ipynb» на гитлаб или

    Задача «Minimum Permutation Group Base»©

    • Группа G перестановок из n символов.
    • Найти базу для G, т.е. последовательность точек b1, …, bk, такой, что единственный элемент в G фиксирующий все эти bi это идентичное преобразование.
    • Минимизировать размер базы, т.е. k.

    Код в «minimum-permutation-group-base.ipynb» на гитлаб или живьем в лабе

    Задача «Minimum Schedule Length»©

    • Сеть , где
      • граф G=(V,E)
      • емкость на вершинах b: V → N
      • емкость на ребрах c: E → N
      • T — набор токенов , где , и p — это либо путь из u в v или пустое множество.
    • Найти расписание S, т.е. последовательность f0, …, fl конфигурационных функций , таких что
      • для любого токена , и .
      • для любого и для любого токена t,
        • если и , то
          • (u,v)∈ E
    • Минимизировать длину расписания, l.

    Код в «minimum-schedule-length.ipynb» на гитлаб или живьем в лабе

    Задача «Maximum Capacity Representatives»©

    • Непересекающиеся множества S1, …, Sm, и для любых , чтобы была задана неотрицательная емкость c(x,y).
    • Найти систему представителей T, т.е. набор T, такой, что для любого i, .
    • Максимизировать «емкость» системы представителей, т.е.

    .

    Код в «maximum-capacity-representatives.ipynb» на гитлаб или

    Задача «Maximum Common Point Set»©

    • Положительный целый d, коллекция S1, …, Sk наборов d-мерных точек.
    • Найти множество точек S' конгруэнтное каждому множеству Si из коллекции.
    • Максимизировать размер этого общего набора точек S'.

    Код в «maximum-common-point-set.ipynb» на гитлаб или

    Задача «Maximum Common Subtree»©

    • Коллекция T1, …, Tn деревьев.
    • Найти дерево T' изоморфное какому-то поддереву, для каждого Ti.
    • Максимизировать число узлов в этом общем поддереве T'.

    Код в «maximum-common-subtree.ipynb» на гитлаб или живьем в лабе

    Задача «Nearest Lattice Vector»©

    • Базис в решетке , где , точка и положительное целое p.
    • Найти вектор b в решетке, не совпадающий с заданным , но ближайший к нему.
    • Минимизировать расстояние между b0 и b, по норме .

    Код в «nearest-lattice-vector.ipynb» на гитлаб или живьем в лабе

    Задача «Shortest Path With Forbidden Pairs»©

    • Граф G=(V,E) и коллекция пар вершин из V, начальная вершина s ∈ V, и конечная вершина f ∈ V.
    • Найти простой путь из s в f, который содержит хотя бы одну вершину из каждой пары в C.
    • Минимизировать длину пути, то есть количество ребер в пути.

    Код в «shortest-path-with-forbidden-pairs.ipynb» на гитлаб или живьем в лабе

    Задача «Shortest Weight-Constrained Path»©

    • Граф G=(V,E), длина l: E → N, и вес w: E → N ребер,

    выделенные вершины и целое W.

    • Найти простой путь в G весом не больше W, т.е. последовательность различных вершин , таких, что и .
    • Минимизировать длину этого пути, т.е. .

    Код в «shortest-weight-constrained-path.ipynb» на гитлаб или живьем в лабе

    Задача «Minimum Vehicle Scheduling On Tree»©

    • Дерево с выделенным корнем ,
      • на ребрах заданы времена проезда в
        • прямом f: E → N
        • обратно направлении b: E → N
      • на вершинах
        • время отгрузки-загрузки r: V → N
        • время обработки h: V → N

    Найти расписание автомобильного объезда, которое

    • стартует в v0,
    • посещает все вершины в
    • возвращается в v0
    • для любой вершины
      • обработка стартует не раньше .

    Т.е. найти перестановку вершин , и функция ожидания w, такую что для любого i где d(u,v) означает длину уникального пути из u в v.


    Минимизировать полное время выполнения, т.е.

    Код в «minimum-vehicle-scheduling-on-tree.ipynb» на гитлаб или живьем в лабе

    Задача «Minimum Point-To-Point Connection»©

    • Граф G=(V,E), веса на ребрах w: E → N и множество стартовых и финишных точек.
    • Найти связь точка-точка, т.е. подмножество ребер E' ⊆ E, таких, что для каждой пары старт-финиш, можно проложить путь в E'.
    • Минимизировать вес этой связи, .

    Код в «minimum-point-to-point-connection.ipynb» на гитлаб или живьем в лабе

    Задача «Minimum Linear Arrangement»©

    • Граф G=(V,E).
    • Найти линейное упорядочивание V, т.е. биективную функцию .
    • Минимизировать сумму длин ребер в этом упорядочивании, т.е. .

    Код в «minimum-linear-arrangement.ipynb» на гитлаб или живьем в лабе

    Задача «Minimum K-Switching Network»©

    • Полный граф G=(V,E), расстояния удовлетворяющие неравенство треугольника.
    • Разбиение вершин V.
    • Минимизировать максимальное расстояние между вершинами разных множеств с одним индексом, т.е.

    Код в «minimum-k-switching-network.ipynb» на гитлаб или живьем в лабе

    Задача «Minimum Complete Bipartite Subgraph Cover»©

    Граф G=(V,E).

    Найти полное покрытие двудольными подграфами G, т.е. коллекцию

    подмножеств вершин V → , такую, что

    • каждое такое подмножество вершин Vi порождает полный двудольный граф.
    • каждое ребро (u,v) ∈ E содержит оба конца в каком-нибудь Vi

    Минимизировать «k» — размер этого покрытия.

    Код в «minimum-complete-bipartite-subgraph-cover.ipynb» на гитлаб или живьем в лабе

    Задача «Minimum Bottleneck Path Matching»©

    Граф G=(V,E) с четным числом вершин, и весами на ребрах: w: E → N.

    Найти непересекающиеся по пути совершенные сочетания для G, т.е. коллекция

    непересекающихся простых путей в G с различными финишными вершинами.

    Минимизировать вес самого «тяжелого» пути в этих сочетаниях, т.е.

    Код в «minimum-bottleneck-path-matching.ipynb» на гитлаб или живьем в лабе

    Задача «Minimum Bandwidth»©

    • Граф G=(V,E).
    • Найти линейное упорядочивание V, т.е. биективную функцию .
    • Минимизировать «пропускную способность» этого упорядочивания, т.е. .

    Код в «minimum-bandwidth.ipynb» на гитлаб или живьем в лабе

    Задача «Maximum Priority Flow»©

    • Направленный граф G=(V,E), вершины-источники , вершины-стоки , емкость ребер c: E → R, ограничения на вершинах b: V → R, и для любой вершины v, есть некий порядок исходящих ребер.
    • Найти приоритетный поток f, т.е. функция f: E→R, такая что
      • для любого ребра e, f(e) ≤ c(e)
      • для любой вершины , поток сохраняется в v
      • для любой вершины v
        • поток покидающий v не превышает b(v)
        • для исходящей любой пары ребер , если и , то .
    • Максимизировать поток, приходящей в первый сток t1, т.е. .

    Код в «maximum-priority-flow.ipynb» на гитлаб или живьем в лабе

    Задача «Maximum Satisfiability Of Quadratic Equations Over Gf(Q)»©

    • Простое число q, набор полиномов степени не большей 2, над полем GF[q] от n переменных. Эти полиномы не должны содержать мономов .
    • Найти в подмножество полиномов P'⊆ P, у которых будет некий общий корень.
    • Максимизировать размер этого подмножества, т.е. P'.

    Код в «maximum-satisfiability-of-quadratic-equations-over-gf(q).ipynb» на гитлаб или живьем в лабе

    Задача «Longest Path With Forbidden Pairs»©

    • Граф G=(V,E) и коллекция пар вершин из V.
    • Найти простой путь в G, который содержит хотя бы одну вершину из каждой пары в C.
    • Минимизировать длину пути, то есть количество ребер в пути.

    Код в «longest-path-with-forbidden-pairs.ipynb» на гитлаб или

    Задача «Minimum Chordal Graph Completion»©

    • Граф G=(V,E).
    • Найти «хордальный граф», который содержит G, как подграф, т.е. E ⊆ E'.
    • Минимизировать размер хордального графа, |E'|.

    Код в «minimum-chordal-graph-completion.ipynb» на гитлаб или

    Задача «Minimum Interval Graph Completion»©

    • Граф G=(V,E).
    • Найти интервальный граф, который содержит G, как подграф, т.е. E ⊆ E'.
    • Минимизировать размер интервального графа, |E'|.

    Код в «minimum-interval-graph-completion.ipynb» на гитлаб или

    Задача «Minimum Independent Dominating Set»©

    • Граф G=(V,E).
    • Найти независимый доминирующий набор вершин G, т.е. подмножество V'⊆V, такое, что для всех u ∈ V-V' есть
    • v ∈ V'
    • ребро (u,v)∈ E,
    • и при этом нет двух вершин в V' соединенных ребром из E.

    Минимизировать мощность доминирующего набора вершин, |V'|.

    Код в «minimum-independent-dominating-set.ipynb» на гитлаб или живьем в лабе

    Задача «Minimum Job Shop Scheduling»©

    • процессоров (станков, рабочих мест и т.п.), набор работ J, каждая работа j∈J
      • состоит из последовательности из nj операций с , для каждой такой операции
        • требуется процессор
        • и длина .
    • Найти «расписание работы цеха» для J, набор однопроцессорных расписаний, , такое, что
      • из следует
    • Минимизировать время выполнения расписания, т.е.

    Код в «minimum-job-shop-scheduling.ipynb» на гитлаб или живьем в лабе

    Задача «Minimum Ratio-Cut»©

    • Граф G=(V,E), пропускная способность на ребрах c: E → N, k

    товаров, т.е., k пар , и запросы di для каждой пары.

    • Найти разрез, т.е. разбиение V на два непересекающихся набора V1 и V2.
    • Минимизировать емкость разреза деленную на объем запросов через этот разрез:

    Код в «minimum-ratio-cut.ipynb» на гитлаб или живьем в лабе

    Задача «Minimum Resource Constrained Scheduling»©

    • Набор задач T с длинами l(t), m процессоров, число ресурсов , ресурсные потребности задач и ресурсные ограничения bi.
    • Найти m-процессорное расписание для T, соблюдающую ресурсные ограничения, т.е. функцию f: T → Z, такую что
      • , если S(u) будет набор задач t для которых , то и
    • Минимизировать общую длительность расписания, т.е.

    Код в «minimum-resource-constrained-scheduling.ipynb» на гитлаб или живьем в лабе

    Задача «Minimum Time-Cost Tradeoff»©

    • Набор активностей J, направленный ациклический граф определяющий отношения предшествования для активностей, , длительности , положительный бюджет B, и для каждой активности j ∈ J задана монотонно невозрастающая ступенчатая функция с lj ступенями:

    , где .

    • Найти однопроцессорное расписание для J которое соблюдает отношения предшествования, длительности задач и укладывается в бюджет .

    StasFomin 07:13, 12 апреля 2023 (UTC): Что-то на первый взгляд очень странное, штраф за первую задачу всегда будет бесконечным, непонятно.

    • Минимизировать общее время всех активностей

    Код в «minimum-time-cost-tradeoff.ipynb» на гитлаб или

    Задача «Minimum Diameters Decomposition»©

    • Граф G=(V,E).
    • Декомпозиция графа на два фактора F1 и F2 с одинаковыми диаметрами.
    • Минимизация диаметра F1.

    Код в «minimum-diameters-decomposition.ipynb» на гитлаб или живьем в лабе

    Задача «Minimum Edge Dominating Set»©

    Граф G=(V,E).

    Найти доминирующий набор ребер G, т.е. подмножество E' ⊆ E, такое, что для всех

    , где , такой что e1 и e2 совместны.

    Минимизировать мощность доминирующего набора ребер |E'|

    Код в «minimum-edge-dominating-set.ipynb» на гитлаб или живьем в лабе

    Задача «Minimum Height Two Dimensional Packing»©

    • Набор прямоугольников с положительными размерами (ширина , высота yi).
    • Найти упаковку из прямоугольников B в плоский контейнер единичной ширины и бесконечной высоты. Прямоугольники должны быть упакованы без пересечений и вращать их нельзя.
    • Минимизировать высоту упаковку P.

    Код в «minimum-height-two-dimensional-packing.ipynb» на гитлаб или живьем в лабе

    Задача «Minimum 3-Dedicated Processor Scheduling»©

    • Набор задач T, набор P из 3 процессоров, каждая задача t ∈ T имеет
      • длительность
      • требуемое подмножество процессоров r(t)⊆P .
    • Найти расписание для T, т.е. функция возвращающая время старта , такую что для любых двух задач t1 и t2, у которых , либо
    • Минимизировать полное время расписания

    Код в «minimum-3-dedicated-processor-scheduling.ipynb» на гитлаб или живьем в лабе

    Задача «Minimum Broadcast Time»©

    • Граф G=(V,E), вершина-источник .
    • Найти схему вещания. В момент «0» только v0 содержит сообщение, которое надо передать в кажду вершину. В каждый момент любая вершина, котора получила сообщение, может передать это сообщение максимум одному из своих соседей.
    • Минимизировать время передачи, т.е. момент времени, когда все вершины получат сообщение.

    Код в «minimum-broadcast-time.ipynb» на гитлаб или живьем в лабе

    Задача «Maximum Constrained Partition»©

    • Конечное множество A и размер для каждого его элемента a ∈ A, выделенный элемент , и подмножество S⊆A.
    • Найти разбиение A, т.е. подмножество A' ⊆ A, такой, что
    • число элементов из S на той стороне разбиения, где a0.

    Код в «maximum-constrained-partition.ipynb» на гитлаб или живьем в лабе

    Задача «Maximum Hyperplane Consistency»©

    • Конечные множества P и N целочисленных n-мерных векторов.
      • P — положительные примеры
      • N — отрицательные примеры.
    • Найти гиперплоскость заданную вектором нормали и смещением w0.
    • Максимизировать число примеров, удовлетворяющих этой гиперплоскости:
    .

    Код в «maximum-hyperplane-consistency.ipynb» на гитлаб или

    Задача «Maximum Common Embedded Sub-Tree»©

    • Деревья T1 и T2 с метками на вершинах.
    • Найти общее встроенное поддерево, т.е. помеченное дерево T', которое можно встроить в оба исходных дерева. Встраивание из T' в T, это инъективная функция от вершин T' в вершины T, которая сохраняет метки и отношения предшествования (пропускать предшественников можно).
    • Максимизировать размер общего поддерева, |T'|.

    Код в «maximum-common-embedded-sub-tree.ipynb» на гитлаб или живьем в лабе

    Задача «Minimum Geometric 3-Degree Spanning Tree»©

    • Множество P ⊆ Z×Z точек на плоскости.
    • Найти остовное дерево T для P, в котором нет вершин степени большей 3.
    • Минимизировать полный вес этого дерева, , где d(u,v) — евклидово расстояние между u и v.

    Код в «minimum-geometric-3-degree-spanning-tree.ipynb» на гитлаб или живьем в лабе

    Задача «Minimum Geometric Disk Cover»©

    • Множество точек на целочисленной плоскости P ⊆ Z×Z.
    • Найти набор центров C ⊆ Q×Q на Евклидовой плоскости, такой, что каждая точка в P будет покрыта диском с радиусом и центром в одной из точек в C.
    • Минимизировать размер этого дискового покрытия, т.е.

    Код в «minimum-geometric-disk-cover.ipynb» на гитлаб или живьем в лабе

    Задача «Minimum Geometric Steiner Tree»©

    • Набор точек на плоскости P ⊆ Z×Z.
    • Найти конечный набор точек Штейнера, Q ⊆ Z×Z.
    • Минимизировать полный вес минимального остовного дерева для набора вершин , где вес ребра это округленная евклидова длина

    Код в «minimum-geometric-steiner-tree.ipynb» на гитлаб или живьем в лабе

    Задача «Minimum Multi Cut»©

    • Граф G=(V,E), набор S ⊆ V×V пар «источник-терминал», веса на ребрах w: E → N.
    • Найти мультиразрез, т.е. набор ребер E' ⊆ E, удаление которых отсоединит каждый терминал от своего источника.
    • Минимизировать вес разреза, т.е. .

    Код в «minimum-multi-cut.ipynb» на гитлаб или живьем в лабе

    Задача «Minimum Generalized Steiner Network»©

    • Граф G=(V,E), веса w: E → N и пропускная способность c: E → N на ребрах, функция требований r: V×V → N.
    • Найти сеть Штейнера над G которая удовлетворит требованиям, не превысив пропускные способности, т.е. функция f: E → N, такая, что для каждого ребра e, и для любой пары вершин i и j, число непересекающихся по ребрам путей между i и j будет как минимум r(i,j), при этом, для кадого ребра e можно использовать f(e) копий ребра e.
    • Минимизировать .

    Код в «minimum-generalized-steiner-network.ipynb» на гитлаб или живьем в лабе

    Задача «Minimum Strong Connectivity Augmentation»©

    • Направленный граф G=(V,A), и весовая функция w: V×V → N.
    • Найти набор дуг A' дополнения G до связности, т.е. A' — упорядоченные пары вершин из V, такие что сильно связан.
    • Минимизировать вес дополняющего набора .

    Код в «minimum-strong-connectivity-augmentation.ipynb» на гитлаб или живьем в лабе

    Задача «Minimum Sequencing With Release Times»©

    • Набор задач T, для каждой задачи есть
      • время релиза (раньше запускать задачу нельзя)
      • длина
      • вес
    • Найти однопроцессорное расписание для T, которое соблюдает времена релиза, т.е. функция f: T → N, которая
      • , если S(u) это набор задач t, для которых , то (в процессе только одна задача)
      • (раньше релиза не запускаем)
    • Минимизировать взвешенную сумму времен завершения

    Код в «minimum-sequencing-with-release-times.ipynb» на гитлаб или живьем в лабе

    Задача «Minimum Single Sink Edge Installation»©

    • Граф G=(V,E), пути на ребрах l: E → N, набор вершин-источников S⊆V, сток t ∈ V, функция запросов , конечный набор типов кабелей, характеризующихся емкостью и стоимостью единицы длины.
    • Найти сеть из этих кабелей, т.е. количество кабелей каждого типа для каждого ребра, причем такое, чтобы выполнить все запросы из источников к стоку. Запрос каждого источника должен идти по одному пути от источника к стоку.
    • Минимизировать полную стоимость этой сети.

    Код в «minimum-single-sink-edge-installation.ipynb» на гитлаб или

    Задача «Minimum Steiner Tree»©

    • Полный граф G=(V,E), метрика — веса на ребрах s: E → N, некоторое подмножество S⊆V требуемых вершин.
    • Найти дерево Штейнера, т.е. поддерево G которое включает все вершины из S.
    • Минимизировать сумму весов ребер этого поддерево.

    Код в «minimum-steiner-tree.ipynb» на гитлаб или живьем в лабе

    Задача «Minimum File Transfer Scheduling»©

    • Граф передачи файла, т.е. граф G=(V,E), ограничения пропускной способности на вершинах, p: V → N и функция длины файлов на ребрах L: E → N.
    • Найти расписание передачи файла, т.е. функция s: E → N, такая что для каждой вершины v и для каждого момента t ∈ N,
    • Минимизировать время выполнения расписания, т.е.

    Код в «minimum-file-transfer-scheduling.ipynb» на гитлаб или живьем в лабе

    Задача «Minimum Multiway Cut»©

    • Граф G=(V,E), набор S⊆V терминалов, веса на ребрах w: E → N.
    • Многопутевой разрез, т.е. набор ребер E' ⊆ E, удаление которых отсоединит каждый терминал от других.
    • Минимизировать вес разреза, т.е. .

    Код в «minimum-multiway-cut.ipynb» на гитлаб или живьем в лабе

    Задача «Minimum Network Inhibition On Planar Graphs»©

    • Граф G=(V,E), пропускная способность ребер c: E → N, стоимость разрушения ребра d: E → N, и бюджет B.
    • Найти стратегию атаки на эту сеть, т.е. функцию , такую, что .
    • Минимизировать пропускную способность поврежденной сети, т.е. минимальный разрез в G с емкостью .

    Код в «minimum-network-inhibition-on-planar-graphs.ipynb» на гитлаб или живьем в лабе

    Задача «Minimum Precedence Constrained Scheduling»©

    • Набор задач T, m процессоров, единичная время-длина , частичный подрядок предшествования на T.
    • Найти m-процессорное расписание для T, соблюдающую отношения предшествования, т.е. функцию f: T → N, такую что
      • из t < t' следует f(t') > f.
    • Минимизировать время выполнения расписания, т.е.

    Код в «minimum-precedence-constrained-scheduling.ipynb» на гитлаб или живьем в лабе

    Задача «Minimum Quotient Cut»©

    • Граф G=(V,E), веса на вершинах w: V → N, стоимости на ребрах c: E → N.
    • Найти разрез C⊆V.
    • Минимизировать коэффициент разреза, т.е.

    , где c(C) означает сумму стоимостей ребер (u,v), таких, что либо u ∈ C и v ∉ C или u ∉ C и v ∈ C и для любого подмножества V'⊆V, w(V') означает сумму весов вершин из V'.

    Код в «minimum-quotient-cut.ipynb» на гитлаб или

    Задача «Maximum Horn Core»©

    • M — набор булевых значений для n переменных.
    • Найти «Horn core» от M, т.е. подмножество M' ⊆ M, такое, что M' набор булевых значений удовлетворяющих формулу Хорна, [1].
    • Размерность ядра, т.е. |M'|.

    Код в «maximum-horn-core.ipynb» на гитлаб или живьем в лабе

    Задача «Minimum Facility Location»©

    • Полный граф G=(V,E), стоимости перемещения , с неравенством треугольника, F⊆V — места, где можно построить место обслуживания (туалеты, магазины, заправки), — стоимость этого строительства, — потребности в разных местах.
    • Найти места для строительства мест обслуживания, F' ⊆ F.
    • Минимизировать

    Код в «minimum-facility-location.ipynb» на гитлаб или живьем в лабе

    Задача «Minimum Hitting Set»©

    • Коллекция C подмножеств конечного множества S.
    • Найти множество представителей (hitting set) для C, т.е. подмножество S' ⊆ S, такое, что S' содержит по крайней мере один элемент из каждого подмножества из C.
    • Минимизировать размер множества представителей, .

    Код в «minimum-hitting-set.ipynb» на гитлаб или живьем в лабе

    Задача «Minimum Open-Shop Scheduling»©

    • процессоров, множество работ, каждый j ∈ J состоит
      • m операций ( должна выполняться на процессоре i)
      • для каждой такой операции есть длительность .
    • Найти «расписание работы цеха» для J, т.е. коллекцию однопроцессных расписаний ,
      • таких, что из следует , т.е. для каждого j ∈ J, интервалы не пересекаются.
    • Минимизировать время выполнения расписания, т.е.

    Код в «minimum-open-shop-scheduling.ipynb» на гитлаб или живьем в лабе

    Задача «Minimum Planar Record Packing»©

    • Коллекция C из n записей,
      • для каждой записи c ∈ C задана некоторая вероятность p(c), .
    • Найти для каждой записи из c ∈ C размещение z(c) на плоскости, заданное целочисленными координатами, так, что все записи расположены на разных точках этой плоскости.
    • Минимизировать 
    ,

    где — дискретное евклидово расстояние между точками и .

    Код в «minimum-planar-record-packing.ipynb» на гитлаб или живьем в лабе

    Задача «Minimum Traveling Repairman»©

    • Граф G=(V,E), стартовая вершина r ∈ V, длины на ребрах , удовлетворяющие неравенству треугольника.
    • Найти обход, стартующий в r, обходящий все вершины в G, т.е. перестановка , такая что .
    • Минимизировать , где — полное расстояние пройденное в этом пути от стартовой вершины, до вершины v.

    Код в «minimum-traveling-repairman.ipynb» на гитлаб или живьем в лабе

    Задача «Minimum Tree Width»©

    • Граф G=(V,E).
    • Декомпозиция на деревья, т.е. пара , где — некое дерево, и коллекция подмножеств вершин V, такая, что
      • для любого существует
      • для любого v ∈ V множество образует связное поддерево T.
    • Минимизировать ширину дерева в декомпозиции на деревья, т.е. .

    Код в «minimum-tree-width.ipynb» на гитлаб или живьем в лабе

    Задача «Maximum Weighted Satisfiability With Bound»©

    • Набор булевых переменных U, булевое выражение F над U, неотрицательное число-ограничение B ∈ N,
      • для каждой переменной u ∈ U, задан вес , такой что .
    • Найти значения переменных для U, т.е. выбор подмножества U'⊆ U переменных которых выставили в «истину», а остальные U-U' соответственно выставлены в «ложь». Значение решения R будет
      • либо B, если F ложно
      • либо , если F истинно.
    • Максимизировать R.

    Код в «maximum-weighted-satisfiability-with-bound.ipynb» на гитлаб или живьем в лабе

    Задача «Minimum Dynamic Storage Allocation»©

    • Нужно хранить некий набор A каких-то штук, каждая a ∈ A из которых имеет
      • размер
      • время прибытия
      • время отбытия
    • Найти допустимый план резервирования места хранения, т.е. функция , такая что для любых a,a'∈ A, если непусто, то либо , либо .
    • Минимизировать максимальный требуемый размер, т.е.
    .

    Код в «minimum-dynamic-storage-allocation.ipynb» на гитлаб или живьем в лабе

    Задача «Minimum Flow-Shop Scheduling»©

    • процессоров, множество работ, каждый j ∈ J состоит
      • m операций ( должна выполняться на процессоре i)
      • для каждой такой операции есть длительность .
    • Найти «расписание работы цеха» для J (см. Hardprob/Minimum_Open-Shop_Scheduling), такая что, для каждого j ∈ J, и , .
    • Минимизировать время выполнения расписания, т.е.


    Код в «minimum-flow-shop-scheduling.ipynb» на гитлаб или

    Задача «Minimum Graph Motion Planning»©

    • Граф G=(V,E),
      • стартовая вершина s ∈ V, где изначально размещается робот,
      • целевая вершина t ∈ V
      • подмножество вершин W⊆V где изначально находятся препятствия.
    • Найти схему движения робота и этих препятствий. На каждом шагу, либо робот, либо одно препятствие можно переместить на незанятую вершину. Надо переместить робота в целевую вершину.
    • Минимизировать число шагов.

    Код в «minimum-graph-motion-planning.ipynb» на гитлаб или живьем в лабе

    Задача «Minimum K-Supplier»©

    • Полный граф G=(V,E), расстояния , удовлетворяющие неравенству треугольника, для вершин v ∈ V заданы стоимость строительство центра , некий «вес» использования , ограничение на бюджет L ∈ N.
    • Места размещения поставок в рамках бюджета, т.е. подмножество вершин S⊆V, для которых .
    • Минимизировать максимальную взвешенную дистанцию от вершины до ближайшего поставщика, т.е.

    Код в «minimum-k-supplier.ipynb» на гитлаб или живьем в лабе

    Задача «Minimum Metric Bottleneck Wandering Salesperson Problem»©

    • Набор C из m городов, стартовый город s ∈ C, финишный город f ∈ C, расстояния удовлетворяющие неравенству треугольника.
    • Найти простой путь из начального города s в финишный город f проходящий через все города из C, т.е. перестановка , такая что и .
    • Минимизировать максимальную длину ребра в пути.

    Код в «minimum-metric-bottleneck-wandering-salesperson-problem.ipynb» на гитлаб или живьем в лабе

    Задача «Minimum Metric Traveling K-Salesperson Problem»©

    • Набор C из m городов, стартовый город s ∈ C, расстояния удовлетворяющие неравенству треугольника.
    • Найти коллекцию из k подтуров, каждый из которых соедержит начальный город, и каждый город есть хотя бы в одном подтуре.
    • Минимизировать максимальную длину среди этих k подтуров.

    Код в «minimum-metric-traveling-k-salesperson-problem.ipynb» на гитлаб или

    Задача «Minimum Edge Deletion To Obtain Subgraph With Property P»©

    • Направленный или ненаправленный граф G=(V,E) и некое свойство (предикат) P над подграфами.
    • Найти подмножество ребер E' ⊆ E, такое, что подграф G=(V, E-E') имеет свойство P.
    • Минимизировать размер этого удаляемого множества ребер |E'|.

    Код в «minimum-edge-deletion-to-obtain-subgraph-with-property-p.ipynb» на гитлаб или живьем в лабе

    Задача «Minimum Edge Deletion K-Partition»©

    • Граф G=(V,E), с весом на ребрах w: E → N.
    • Найти «k»-разбиение вершин («раскраску») c: V → [1..k]
    • Минимизировать вес одноцветных ребер, т.е. .

    Код в «minimum-edge-deletion-k-partition.ipynb» на гитлаб или живьем в лабе

    Задача «Maximum Constrained Sequencing To Minimize Tardy Task Weight»©

    • Набор T задач, для каждой задачи t ∈ T есть длина , вес и дедлайн , подмножество S ⊆ T и положительное целое K.
    • Найти однопроцессорное расписание σ для T, такая что сумма w(t) по всем t ∈ T для которых не превосходит K.
    • Максимизировать число работ в S, выполненных в срок.

    Код в «maximum-constrained-sequencing-to-minimize-tardy-task-weight.ipynb» на гитлаб или

    Задача «Minimum Dominating Set»©

    • Граф G=(V,E).
    • Найти «доминирующий набор» для G, то есть подмножество V'⊆V такое что для всех u ∈ V-V' cуществует v ∈ V' для которого (u,v) ∈ E.
    • Оптимизировать «кардинальность доминирующего набора», то есть, |V'| → min.

    Код в «minimum-dominating-set.ipynb» на гитлаб или живьем в лабе

    Задача «Minimum Directed Bandwidth»©

    • Направленный ациклический граф G=(V,E).
    • Найти линейное упорядочивание V, т.е. биективную функцию f: V→ {1,2,…,|V|}, такую что (u,v)∈ E, f(u)<f(v).
    • Минимизировать «пропускную способность» этого упорядочивания, т.е. .

    Код в «minimum-directed-bandwidth.ipynb» на гитлаб или живьем в лабе

    Задача «Minimum Diameter Spanning Subgraph»©

    • Граф G=(V,E), на ребрах e ∈ E заданы вес и длина l(e)∈ N, положительное число B.
    • Найти остовный подграф E' ⊆ E для G, такой, что сумма весов ребер в E' не превосходит B.
    • Минимизировать диаметр остовного подграфа.

    Код в «minimum-diameter-spanning-subgraph.ipynb» на гитлаб или живьем в лабе

    Задача «Minimum K-Stacker Crane Problem»©

    • Смешанный (ориентированные дуги и неориентированные ребра) граф , длины на ребрах l(e)∈ N для каждого ребра и дуги .
    • Найти коллекцию из k циклов, каждый содержит начальную вершину s, такая, что их совокупность включает каждое дугу графа.
    • Минимизировать максимальную длину среди этих k циклов.

    Код в «minimum-k-stacker-crane-problem.ipynb» на гитлаб или живьем в лабе

    Задача «Minimum Stacker Crane Problem»©

    • Смешанный (ориентированные дуги и неориентированные ребра) граф , длины на ребрах l(e)∈ N для каждого ребра и дуги , такой, что для каждой дуги, есть параллельное ребро где длина не больше.
    • Найти цикл в G (возможно с повтором вершин), такой что включает каждое направленную дугу в A по крайней мере один раз, проходя по ним в правильном направлении.
    • Минимизировать тотальную длину цикла.

    Код в «minimum-stacker-crane-problem.ipynb» на гитлаб или живьем в лабе

    Задача «Minimum Vertex Cover»©

    Граф .

    Найти, «вершинное покрытие» для «G», т.е.подмножество V'⊆V, такое, что

    для каждого ребра (u,v)∈ E, по меньшей мере одна вершина — «u» или «v» принадлежит V'.

    Оптимизируем размерность вершинного покрытия, т.е. |V'|

    Код в «minimum-vertex-cover.ipynb» на гитлаб или

    Задача «Minimum Crossing Number»©

    • Направленный граф G=(V,A).
    • Найти размещение графа на плоскости.
    • Минимизируя число пересекающихся пар ребер.

    Код в «minimum-crossing-number.ipynb» на гитлаб или живьем в лабе

    Задача «Minimum Feedback Arc Set»©

    Направленный граф G=(V,A).

    Найти множество ребер разрезающее циклы,

    т.е. подмножество , такое, что A' содержит по крайней мере одну дугу из каждого направленного цикла в G.

    Минимизировать размерность этого подмножества, .

    Код в «minimum-feedback-arc-set.ipynb» на гитлаб или живьем в лабе

    Задача «Minimum Feedback Vertex Set»©

    Направленный граф G=(V,A).

    Найти множество вершин разрезающее циклы,

    т.е. подмножество , такое, что V' содержит по крайней мере одну вершину из каждого направленного цикла в G.

    Минимизировать размерность этого подмножества, |V'|.

    Код в «minimum-feedback-vertex-set.ipynb» на гитлаб или живьем в лабе

    Задача «Minimum Communication Cost Spanning Tree»©

    • Полный граф G=(V,E), веса на ребрах w(e)∈N, e∈E, некоторое требование для каждой пары вершин r({u,v})∈N.
    • Найти основное дерево для G.
    • Минимизировать взвешенную сумму по всем парам вершин стоимостей путей по парам вершин в T, т.е., , где W(u,v) означает сумму весов ребере на пути, соединающем u и v в T.

    Код в «minimum-communication-cost-spanning-tree.ipynb» на гитлаб или живьем в лабе

    Задача «Minimum Precedence Constrained Sequencing With Delays»©

    • Набор задач T, положительное целое D, для каждой задачи есть целочисленная задержка ,
      • направленный ациклический граф , определяющий отношения предшествования для этих задач.
    • Найти одно-процессорное расписание для T, соблюдающее отношения предшествования и задержки, т.е. инъективная функция , такая, что для каждого ребра , выполняется
    • Минимизировать время выполнение всего расписания.

    Код в «minimum-precedence-constrained-sequencing-with-delays.ipynb» на гитлаб или живьем в лабе

    Задача «Minimum Generalized 0-1 Assignment»©

    • Целая m×n-матрица , целый m-вектор и целая m×n-матрица .
    • Найти m×n-матрицу , в которой только одна единица в каждой колонке, и

    .

    • Минимизировать 
    .

    Код в «minimum-generalized-0-1-assignment.ipynb» на гитлаб или живьем в лабе

    Задача «Minimum Block-Angular Convex Programming»©

    • K непересекающихся выпуклых компактных множеств, блоков
    • M неотрицательных непрерывных выпуклых функций .
    • Найти положительное число λ, такое что

    • Минимизировать λ.

    Код в «minimum-block-angular-convex-programming.ipynb» на гитлаб или живьем в лабе

    Задача «Minimum Array Partition»©

    • Массив n×n неотрицательных целых A, положительное число p.
    • Найти
      • p-1 горизонтальных делителей
      • p-1 вертикальных делителей
      • разбивающих A на блоков.
    • Минимизировать максимальный «вес» блока

    Код в «minimum-array-partition.ipynb» на гитлаб или живьем в лабе

    Задача «Minimum Length Triangulation»©

    • Коллекция пар целых, задающих координаты на плоскости.
    • Найти триангуляцию набора точек из C, т.е. коллекция E непересекающихся отрезков соединающих некоторые точки из C, так, что внутренность этой выпуклой оболочки подразделена на треугольники.
    • Минимизировать округленно-евклидову длину триангуляции, т.е.

    Код в «minimum-length-triangulation.ipynb» на гитлаб или живьем в лабе

    Задача «Minimum K-Spanning Tree»©

    • Граф G=(V,E), целое , веса на ребрах w: E → N.
    • Найти k-остовное дерево, т.е. дерево T, подграф G с по крайней мере k вершинами.
    • Минимизировать вес этогго дерева .

    Код в «minimum-k-spanning-tree.ipynb» на гитлаб или

    Задача «Minimum Chinese Postman For Mixed Graphs»©

    • Мультиграф, начальная вершина s∈V, длина l(e)∈N для каждого ребра e ∈ E.
    • Найти коллекцию из k циклов, каждый содержит начальную вершину s, такая, что их совокупность включает каждое ребро графа.
    • Минимизировать максимальную длину среди этих k циклов.

    Код в «minimum-chinese-postman-for-mixed-graphs.ipynb» на гитлаб или живьем в лабе

    Задача «Minimum Two-Processor Flow Shop Scheduling With Batch Set-Up Times»©

    такой, что для если две операции и , с распланированы последовательно (т.е. нет другой операции , для которой ), и требуют разных компиляторов (т.е. ), то .

    • Минимизировать время выполнения расписания, т.е.
    .

    Код в «minimum-two-processor-flow-shop-scheduling-with-batch-set-up-times.ipynb» на гитлаб или живьем в лабе

    Задача «Minimum Unsatisfying Linear Subsystem»©

    • Система линейных уравнений Ax=b, где A целочисленная m×n—матрица, и целочисленный m-вектор b.
    • Найти рациональный n-вектор .
    • Минимизировать число уравнений, которые не выполняются найденным x.

    Код в «minimum-unsatisfying-linear-subsystem.ipynb» на гитлаб или живьем в лабе

    Задача «Minimum Tree Compact Packing»©

    • Дерево T=(V,E),
      • нормализованный вес на вершинах , ,
      • некоторая страничная емкость p.
    • Найти компактную упаковку T на страницах емкости p, т.е. функция , такая, что
    • Минимизировать страничные сбои этой упаковки, т.е.

    , где

    Код в «minimum-tree-compact-packing.ipynb» на гитлаб или живьем в лабе

    Задача «Minimum Storage Time Sequencing»©

    • Набор задач T, для каждой задачи есть длина ,
      • направленный ациклический граф , определяющий отношения предшествования для этих задач, для каждого ребра этого графа есть вес , измеряющий некий объем хранения, нужный для передачи промежуточных результатов между этими задачами.
    • Найти одно-процессорное расписание для T, соблюдающее отношения предшествования, т.е. перестановка , такая что для каждого ребра выполняется .
    • Минимизировать произведение затрат на хранение и времени, т.е.

    Код в «minimum-storage-time-sequencing.ipynb» на гитлаб или живьем в лабе

    Задача «Minimum Routing Tree Congestion»©

    • Граф G=(V,E), веса w: E → N на ребрах.
    • Найти маршрутное дерево T для G, т.е. дерево T, для которого все внутренние вершины имеют степень 3, а листья соответствуют вершинам G.
    • Минимизировать перегруженность дерева маршрутизации, т.е. минимум по максимуму для каждого ребра e по , и где

    S — это один из двух связных компонентов, полученных удалением e из T.

    Код в «minimum-routing-tree-congestion.ipynb» на гитлаб или живьем в лабе

    Задача «Minimum Relevant Variables In Linear System»©

    • Целочисленная m×n матрица , целый m-вектор .
    • Рациональный n-вектор , такой что Ax=b.
    • Минимизировать число ненулевых элементов в x.

    Код в «minimum-relevant-variables-in-linear-system.ipynb» на гитлаб или живьем в лабе

    Задача «Minimum Quadratic 0-1 Assignment»©

    • Неотрицательная целая n×n-матрица , неотрицательная целая m×m-матрица .
    • Найти бинарную матрицу -матрицу , такую, что в каждой строке не большое одной единицы, и точно одна единица в каждой колонке.
    • Минимизировать 
    .

    Код в «minimum-quadratic-0-1-assignment.ipynb» на гитлаб или живьем в лабе

    Задача «Minimum Multiprocessor Scheduling With Speed Factors»©

    • Набор задач T, m процессоров…
      • для каждой задачи t ∈ T есть длительность
      • для каждого процессора есть фактор скорости , где s(1)=1 и .
    • Найти m-процессорное расписание для T, т.е. функцию .
    • Минимизировать время завершения расписания, т.е.

    Код в «minimum-multiprocessor-scheduling-with-speed-factors.ipynb» на гитлаб или живьем в лабе

    Задача «Minimum Metric Dimension»©

    • Граф G=(V,E).
    • Найти метрический базис для G, т.е. подмножество V'⊆V, такое, что для каждой пары есть , что длина кратчайшего пути из u в w отличается от длины кратчайшего пути из v в w.
    • Минимизировать размер этого метрического базиса, |V'|.

    Код в «minimum-metric-dimension.ipynb» на гитлаб или живьем в лабе

    Задача «Minimum K-Median»©

    • Полный граф G=(V,E) и расстояния .
    • Найти k-медианное множество, т.е. подмножество .
    • Минимизировать расстояния от каждой вершины до ближайшей медианы, т.е.

    Код в «minimum-k-median.ipynb» на гитлаб или живьем в лабе

    Задача «Minimum K-Center»©

    • Полный граф G=(V,E) и расстояния , удовлетворяющие неравенству треугольника.
    • Найти к-центр, т.е. подмножество , с минимальным расстоянием от всех вершин до какого-то узла из этого множества.
    • Минимизировать максимальное расстояние от каждой вершины до ближайшего к ней «центра»:

    Код в «minimum-k-center.ipynb» на гитлаб или живьем в лабе

    Задача «Minimum Graph Inference»©

    • Класс C ненаправленных графов с раскраской ребер из строки цветов x.
    • Найти граф и простой путь в нем, такой, что строка-последовательность ребер на этом пути как раз будет равна x.
    • Минимизировать размер множества ребер в G.

    Код в «minimum-graph-inference.ipynb» на гитлаб или живьем в лабе

    Задача «Minimum Equivalent Digraph»©

    • Направленный граф G=(V,E).
    • Найти подмножество E' ⊆ E, такое что для каждой пары вершин , граф G'=(V,E') содержит направленный путь из u в v, тогда и только тогда, когда этот путь есть в оригинальном графе G.
    • Минимизировать размер E', т.е. |E'|.

    Код в «minimum-equivalent-digraph.ipynb» на гитлаб или живьем в лабе

    Задача «Minimum Biconnectivity Augmentation»©

    • Граф G=(V,E), и симметричная весовая функция w: V×V → N.
    • Найти набор ребер E' дополнения G до связности, т.е. E' — неупорядоченные пары вершин из V, такие что G'=(V, E ∪ E') двусвязен.
    • Минимизировать вес дополняющего набора .

    Код в «minimum-biconnectivity-augmentation.ipynb» на гитлаб или живьем в лабе

    Задача «Maximum Satisfying Linear Subsystem»©

    • Система линейных уравнений Ax=b, где A целочисленная m×n—матрица, и целочисленный m-вектор b.
    • Найти рациональный n-вектор .
    • Максимизировать число уравнений, которые выполняются найденным x.

    Код в «maximum-satisfying-linear-subsystem.ipynb» на гитлаб или живьем в лабе

    Задача «Maximum Renamable Horn Subformula»©

    • Набор булевых переменных U, коллекция C скобок-конъюнкций не больше чем из трех литералов.
    • Найти переименовываемую хорнову подформулу C' от C, т.е. подмножество C'⊆ C, т.к. здесь существует подмножество S ⊆ U, таких переменных, что перестановка литералов в делает C' хорновой булевой формулы, где .
    • Максимизировать размер подформулы, т.е. |C'|.

    Код в «maximum-renamable-horn-subformula.ipynb» на гитлаб или живьем в лабе

    Задача «Maximum K-Facility Dispersion»©

    • Полный граф G=(V,E), расстояния , с неравенством треугольника.
    • Найти набор для размещения k мест обслуживания (туалеты, магазины, заправки), подмножество .
    • Минимизировать минимальное расстояние между двумя такими местами:

    Код в «maximum-k-facility-dispersion.ipynb» на гитлаб или живьем в лабе

    Задача «Maximum K-Facility Location»©

    • Полный граф G=(V,E), доходы .
    • Найти места для строительства мест обслуживания, .
    • Максимизировать максимальный полный доход

    .

    Код в «maximum-k-facility-location.ipynb» на гитлаб или живьем в лабе

    Задача «Longest Common Subsequence»©

    • Конечный алфавит Σ, конечный набор R строк из .
    • Найти строку , такую она является подпоследовательностью любой строки x ∈ R, т.е. ее можно получить вычеркивая символы из любого x.
    • Максимизировать длину этой подпоследовательности .

    Код в «longest-common-subsequence.ipynb» на гитлаб или живьем в лабе

    Задача «Minimum Bounded Diameter Augmentation»©

    • Граф G=(V,E), положительное целое .
    • Найти дополняющий набор новых ребер E' для G, т.е. набор E' неупорядоченных пар вершин из V, такой что G'=(V, E ∪ E') имеет диаметр D, т.е. максимальное расстояние между любыми парами вершин будет не больше чем D.
    • Минимизировать размер дополняющего множества |E'|.

    Код в «minimum-bounded-diameter-augmentation.ipynb» на гитлаб или живьем в лабе

    Задача «Minimum Rectangle Tiling»©

    • Массив n×n неотрицательных целых A, положительное число p.
    • Найти разбиение A на непересекающихся квадратных подмассивов.
    • Минимизировать максимальный «вес» (сумма элементов) подмассива из разбиения.

    Код в «minimum-rectangle-tiling.ipynb» на гитлаб или живьем в лабе

    Задача «Maximum Quadratic Assignment»©

    • Неотрицательные симметричные n×n матрицы A и B.
    • Найти перестановку .
    • Максимизировать .

    Код в «maximum-quadratic-assignment.ipynb» на гитлаб или живьем в лабе

    Задача «Minimum Rectilinear Global Routing»©

    • -массив шлюзов, коллекция сетей C, т.е. наборов по три шлюза.
    • Найти прямые отрезки-связи соединяющие шлюзи в каждой сети.
    • Минимизировать самое большое число связей, соединающих два шлюза в данном массиве.

    Код в «minimum-rectilinear-global-routing.ipynb» на гитлаб или

    Задача «Maximum Not-All-Equal 3-Satisfiability»©

    • Множество переменных U,
    • Коллекция C скобок-дизъюнкций литералов, где литерал это какая-то переменная или ее отрицание, размер скобки не больше 3.
    • Найти истинное присваивание для U, и подмножество скобок C'⊆ C, таких что каждая скобка имеет по крайней мере один истинный литерал и не меньше одного ложного литерала.
    • Максимизировать размер этого подмножества |C'| → max

    Код в «maximum-not-all-equal-3-satisfiability.ipynb» на гитлаб или

    Задача «Maximum Minimum Spanning Tree Deleting K Edges»©

    • Граф G=(V,E), веса w: E → N на ребрах.
    • Найти подграф E' ⊆ E из k ребер, и минимальное остовное дерево T в графе (V,E-E').
    • Минимизировать вес T.

    Код в «maximum-minimum-spanning-tree-deleting-k-edges.ipynb» на гитлаб или

    Задача «Maximum Minimum Metric K-Spanning Tree»©

    • Граф G=(V,E), длина ребер l(e) ∈ N ∀e∈E удовлетворяют неравенству треугольника.
    • Найти подмножество V'⊆V, такое, что |V'|=k
    • Максимизировать стоимость минимального остовного дерева подграфа, порожденного V'.

    Код в «maximum-minimum-metric-k-spanning-tree.ipynb» на гитлаб или

    Задача «Minimum Maximal Matching»©

    Граф G=(V,E).

    Найти максимальное паросочетание E', т.е. подмножество E' ⊆ E, такое, что

    никакие два ребра не содержат одну вершину, но каждое ребро из E-E' с кем-то содержит общую вершину с каким-либо ребром из E' (т.е. добавить «еще одну пару» нельзя).

    Минимизировать размерность паросочетания |E'|.

    Код в «minimum-maximal-matching.ipynb» на гитлаб или

    Задача «Maximum K-Colorable Subgraph»©

    • Граф G=(V,E).
    • Найти подмножество ребер E' ⊆ E, такое, что подграф G'=(V,E') может быть раскрашен в k-цветов, т.е. есть раскраска G' размерности не больше k.
    • Максимизировать мощность этого подграфа |E'|

    Код в «maximum-k-colorable-subgraph.ipynb» на гитлаб или

    Задача «Maximum Subforest»©

    • Дерево G=(V,E) и набор деревьев H.
    • Найти подмножество ребер E' ⊆ E, такое, что подграф G'=(V,E') не содержит ни одного поддерева изоморфного какому-нибудь дереву из H.
    • Максимизировать мощность этого подграфа |E'|

    Код в «maximum-subforest.ipynb» на гитлаб или

    Задача «Maximum Planar Subgraph»©

    • Граф G=(V,E).
    • Найти подмножество ребер E' ⊆ E, такое что подграф G'=(V,E') — планарный.

    Максимизировать размер этого планарного подграфа, |E'|.

    Код в «maximum-planar-subgraph.ipynb» на гитлаб или

    Задача «Maximum Induced Connected Subgraph With Property P»©

    • Граф G=(V,E) и некое свойство (предикат) P над подграфами.
    • Найти подмножество вершин V'⊆V, такое, что подграф порожденный вершинами V' — связный и имеет свойство P.
    • Максимизировать размер этого множества |V'| → max.

    Код в «maximum-induced-connected-subgraph-with-property-p.ipynb» на гитлаб или

    Задача «Maximum Independent Set»©

    • Граф G=(V,E).
    • Найти независимое множество вершин, т.е. подмножество V'⊆V, такое что нет пары вершин в V', соединенных ребром из E.
    • Максимизировать размер этого независимого множества |V'| → max

    Код в «maximum-independent-set.ipynb» на гитлаб или

    Задача «Minimum Vertex Deletion To Obtain Connected Subgraph With Property P»©

    Направленный или ненаправленныый граф G=(V,E) и некое свойство (предикат) P над подграфами.

    Найти подмножество вершин V'⊆V, такое, что подграф порожденный вершинами V-V' — связный и

    имеет свойство P.

    Минимизировать размер этого множества |V'|.

    Код в «minimum-vertex-deletion-to-obtain-connected-subgraph-with-property-p.ipynb» на гитлаб или

    Задача «Minimum Vertex Deletion To Obtain Subgraph With Property P»©

    Направленный или ненаправленный граф G=(V,E) и некое свойство (предикат) P над подграфами.


    Найти подмножество вершин V'⊆V, такое, что подграф порожденный V-V' имеет свойство P.


    Минимизировать размер этого удаляемого множества вершин |V'|.

    Код в «minimum-vertex-deletion-to-obtain-subgraph-with-property-p.ipynb» на гитлаб или живьем в лабе

    Задача «Maximum K-Colorable Induced Subgraph»©

    • Граф G=(V,E).
    • Найти подмножество V'⊆V, такое, что порожденный подграф k-раскрашиваем, т.е. есть раскраска G', размерности не больше чем k.
    • Минимизировать размер этого подмножества, |V'|.

    Код в «maximum-k-colorable-induced-subgraph.ipynb» на гитлаб или

    Задача «Minimum Vertex Disjoint Cycle Cover»©

    Граф G=(V,E).

    Найти семейство F непересекающихся по вершинам циклов, покрывающих V.

    Минимизировать число этих циклов в F.

    Код в «minimum-vertex-disjoint-cycle-cover.ipynb» на гитлаб или

    Задача «Minimum Bend Number»©

    • Направленный планарный граф G=(V,E)
    • Найти планарный ортогональный чертеж графа G, т.е. отрисовка вершин G как точек плоскости, а ребер как последовательностей горизонтальных и вертикальных отрезков, так, что нет пересечений.
    • Минимизировать число сгибов на чертеже.

    Код в «minimum-bend-number.ipynb» на гитлаб или

    Задача «Maximum Leaf Spanning Tree»©

    • Граф G=(V,E).
    • Найти остовное дерево G.
    • Минимизировать число листьев в этом остовном дереве.

    Код в «maximum-leaf-spanning-tree.ipynb» на гитлаб или

    Задача «Minimum Edge K-Spanner»©

    • Связный граф G=(V,E) с весами на ребрах w: E → N, положительное целое k.
    • Найти k-остов G, т.е. G' — остовной подграф G такой, что для любой пары вершин u и v, длина кратчайшего пути между u и v в G' будет не больше чем в k раз больше, чем кратчайший путь между u и v в исходном графе G.
    • Минимизировать число ребер в G' (вариант — минимизировать сумму весов ребер G').

    Код в «minimum-edge-k-spanner.ipynb» на гитлаб или

    Задача «Minimum Degree Spanning Tree»©

    • Граф G=(V,E).
    • Найти остовное дерево T для G.
    • Минимизировать максимальную степень этого дерева.

    Код в «minimum-degree-spanning-tree.ipynb» на гитлаб или

    Задача «Minimum Locally Testable Automaton Order»©

    • Локально тестируемый язык L, т.е. некий язык L, такой, что положительное целое j, такое что входит или нет строка x в этот язык зависит от …
      • префикса и суффикса x длины j-1,
      • набора подстрок x длины j.
    • Найти порядок j, т.е. положительное целое j, «свидетель» локальной тестируемости L.
    • Минимизировать значение порядка, т.е. j.

    Код в «minimum-locally-testable-automaton-order.ipynb» на гитлаб или живьем в лабе

    Задача «Shortest Computation»©

    • Недетерминированная машина Тьюринга M, двоичная входная строка x.
    • Найти недерминированную строку-догадку c, произведенную машиной M на входе x.
    • Минимизировать длину кратчайшей из этих строк,т.е. .

    Код в «shortest-computation.ipynb» на гитлаб или живьем в лабе

    Задача «Longest Computation»©

    • Недетерминированная машина Тьюринга M, двоичная входная строка x.
    • Найти недерминированную строку-догадку c, произведенную машиной M на входе x.
    • Максимизировать длину кратчайшей из этих строк,т.е. .

    Код в «longest-computation.ipynb» на гитлаб или живьем в лабе

    Задача «Minimum Consistent Finite Automaton»©

    • Два конечных множества P, N двоичных строк.
    • Найти детерминированный конечный автомат , который принимает все строки из P и отвергает все строки из N.
    • Минимизировать число состояний в автомате.

    Код в «minimum-consistent-finite-automaton.ipynb» на гитлаб или

    Задача «Minimum Length Equivalent Frege Proof»©

    • Доказательство Фреге π для некоторой тавтогологии φ.
    • Найти более короткое доказательство Фреге π' для φ, более короткое чем π, т.е. содержащая не больше символов чем π.
    • Минимизировать число символов в π'.

    Код в «minimum-length-equivalent-frege-proof.ipynb» на гитлаб или

    Задача «Maximum K-Constraint Satisfaction»©

    • Набор булевых переменных U, коллекция C конъюнкций, не больше k литералов (литерал — переменная или ее отрицание),
    • Найти присваивание переменным из U.
    • Максимизировать число выполненных скобок-дизъюнкций.

    Код в «maximum-k-constraint-satisfaction.ipynb» на гитлаб или

    Задача «Minimum Equivalence Deletion»©

    • Набор булевых переменных U, коллекция C равенств, т.е. пар литералов над переменными из U.
    • Найти присваивание переменным U.
    • Минимизировать число невыполненных равенств.

    Код в «minimum-equivalence-deletion.ipynb» на гитлаб или

    Задача «Minimum Number Of Satisfiable Formulas»©

    • Набор булевых переменных U, коллекция C 3CNF-формул.
    • Найти присваивание переменным U.
    • Минимизировать число выполненных формул.

    Код в «minimum-number-of-satisfiable-formulas.ipynb» на гитлаб или

    Задача «Maximum Number Of Satisfiable Formulas»©

    • Набор булевых переменных U, коллекция C 3CNF-формул.
    • Найти присваивание переменным U.
    • Максимизировать число выполненных формул.

    Код в «maximum-number-of-satisfiable-formulas.ipynb» на гитлаб или

    Задача «Minimum Distinguished Ones»©

    • Непересекающиеся множества булевых переменных X,Z, коллекция C дизъюнкций не больше чем три литерала, где каждый литерал переменная или отрицание из X∪Z.
    • Найти присваивание для X и Z, чтобы все скобки в C выполнялись.
    • Минимизировать число переменных из Z, которые будут установлены в «истину».

    Код в «minimum-distinguished-ones.ipynb» на гитлаб или

    Задача «Maximum Distinguished Ones»©

    • Непересекающиеся множества булевых переменных X,Z, коллекция C дизъюнкций не больше чем три литерала, где каждый литерал переменная или отрицание из X∪Z.
    • Найти присваивание для X и Z, чтобы все скобки в C выполнялись.
    • Максимизировать число переменных из Z, которые будут установлены в «истину».

    Код в «maximum-distinguished-ones.ipynb» на гитлаб или

    Задача «Minimum 3-Dnf Satisfiability»©

    • Множество переменных U,
    • Коллекция C скобок-конъюнкций литералов, где литерал это какая-то переменная или ее отрицание, размер скобки не больше 3.
    • Найти присваивание для U.
    • Минимизировать число выполненных скобок.

    Код в «minimum-3-dnf-satisfiability.ipynb» на гитлаб или

    Задача «Maximum Satisfiability»©

    • Множество переменных U,
    • Коллекция C скобок-дизъюнкций литералов, где литерал это какая-то переменная или ее отрицание.
    • Найти истинное присваивание для U.
    • Максимизировать число скобок.

    Код в «maximum-satisfiability.ipynb» на гитлаб или

    Задача «Minimum Travel Robot Localization»©

    • Простой многоугольник P и многоугольник видимости V внутри P, где робота станет видно.
    • Найти схему движения робота до момента, когда его станет видно.
    • Минимизировать расстояние пройденного роботом.

    Код в «minimum-travel-robot-localization.ipynb» на гитлаб или

    Задача «Minimum Rectangle Cover»©

    • Произвольный многоугольник P.
    • Найти коллекцию из m прямоугольников, чье объединение точно эквивалентно многоугольнику P.
    • Минимизировать m — число элементов в этой коллекции.

    Код в «minimum-rectangle-cover.ipynb» на гитлаб или живьем в лабе

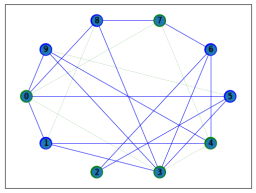
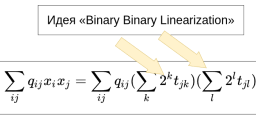
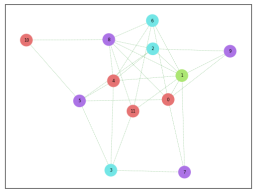
    [ Хронологический вид ]Комментарии

    (нет элементов)

    Войдите, чтобы комментировать.

    Источник — «https://discopal.ispras.ru/index.php?title=Open_Exercises&oldid=26136»