Комментарии — Временная и пространственная сложность алгоритмов/Задачи/QSAT in PSPACE

Решение

Рассмотрим алгоритм проверки выполнимости формулы из QSAT, а затем рассмотрим количество необходимой ему памяти.

Алгоритм:

на фход получаем формулу длины n, имеющую m переменных.

1) привести формулу к виду, в котором все кванторы вынесены перед формулой. Так же заметим, что если какая-то переменная свободна (не под квантором), то выполнимость этой формулы эквивалентна истинности формулы, в которой эта переменная находится под квантором существования.

Итак, имеем формулу, в которой присутствуют m литералов, никакой из которых не является свободным. Назовем P(x) - часть формулы без предикатов.

2) имеем m переменных - число из m битов, проходим его от 0 до 2^m-1 и перебираем все возможные наборы переменных.

Составляем дерево:

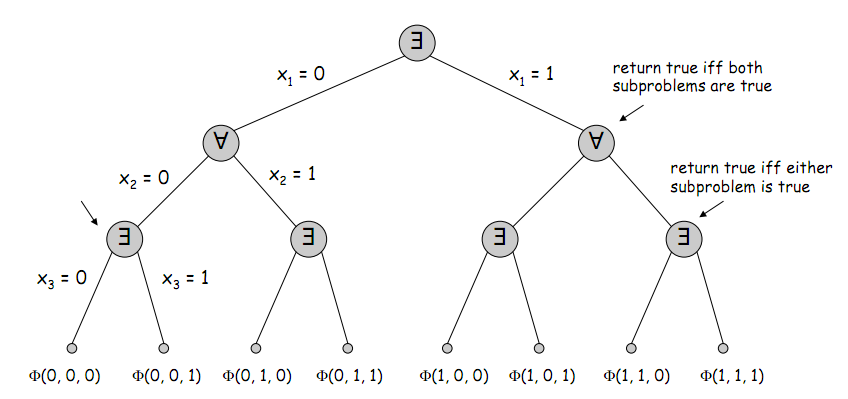
верхний уровень соответствует изменению первой переменной, второй уровень - второй, и так далее. Начинаем обход дерева снизу: вычисляем значение P(x) для первых двух наборов значений переменных, запоминая вычисленные значения (2 бита - a₁ и b₁). Это соответствует различным значениям последней переменной при фиксированных остальных. Теперь если на последней переменной присутствует квантор существования - сохраняем только c₁ = a₁ OR b₁, если всеобщности - c₁ = a₁ AND b₁. Теперь Аналогично вычисляем значение P(x) на следующих двух наборах значений переменных и сохраняем конъюнкцию или дизъюнкцию их значений в c₂. Теперь тем же образом в зависимости от квантора на второй переменной сохраняем только конъюнкцию или дизъюнкцию c₁ и c₂ и так далее...

Если в вершине дерева получим 1 - значит формула выполнима.

Количество используемой памяти: для перебора всех наборов значений переменных - m бит. Для вычисления значения P(x) на фиксированном наборе - не более n бит. При проходе по дереву максимальное количество бит, необходимых для запоминания, равно m. Таким образом, количество необходимой памяти равно m+n+m < 3n бит.

[ Хронологический вид ]Комментарии

(нет элементов)

Войдите, чтобы комментировать.