SocialGraphs/Community Detection
Содержание
[убрать]Community detection and clusterization
Social network analysis examines the structure and composition of ties in the network to answer different questions like:
- Who are the central actors in the network?
- Who has
- the most outgoing connections?
- the most incoming connections?
- the least connections?
- How many actors are involved in passing information through the network?
- Which actors are communicating more often with each others?
The question we are focused here is how one can find communities in a given social network?
First we will list the important terms in a social network analysis and then we will summarize the work related to a community detection in social networks.
- Neighborhood
- of a node consists of its adjacent nodes i.e. the nodes directly connected to it by an edge.
- Clique
- is a subgraph of a network where all the actors are connected to each other.
- Density
- is a measure for how connected the actors are in a network i.e. the proportion of ties in the network divided by the total number of possible ties.
The important question we will address in the rest of this section is how difficult to find communities in a graphs? In fact, the answer depends on formal definition of a community. Today there has not been any consensus on the exact definition of community. Informally speaking the community is a densely connected subset of nodes that is only sparsely linked to the remaining network, a subgraph which is more tightly connected than average. There are different ways to formalize this notion.
The following target function is often used to measure quality of resulting partition of the graph into communities and defines so-called modularity Q of the partition which evaluates the density of links inside communities as compared to links between communities:
where
- Aij represents the weight of the edge between vertexes i and j,
- , is the community to which vertex i is assigned,
- is 1 if u=v and 0 otherwise,
- .
There are other definitions of modularity and quality of community partitions.
Finding a partition of the graph with maximum modularity is NP-hard problem [BrandesDellig2006]. An interesting open problem in this area is to study how good modularity can be efficiently approximated. It is important to stress that similar problems in graph theory (finding maximum clique or chromatic number in a graph) are difficult to approximate [Hastad97], [Hastad1997]. Moreover, such problems may be hard even in random graphs (see, [JuelsPeinado1998], [AlonKrivelevichSudakov1998].
Similar to the notion of community is the notion of a dense subgraph.
Given an undirected graph G = (V, E), the density of a subgraph on vertex set S is defined aswhere E(S) is the set of edges in the subgraph induced by S.
The problem of finding the densest subgraph of a given graph G can be solved optimally in polynomial time (using flow technique), despite the fact that there are exponentially many subgraphs to consider [Gpldberg1984]. In addition, Charikar [Charikar2000] showed that we can find a 2-approximation to the densest subgraph problem in linear time using a very simple greedy algorithm. This result is interesting because in many applications of analyzing social networks, web graphs etc., the size of an graph involved could be very large and so having a fast algorithm for finding an approximately dense subgraph is extremely useful.
However when there is a size constraint specified — namely find a densest subgraph of exactly k vertices, the densest k subgraph problem becomes NP-hard [FeigeKortsarzPeleg1997], [AsahiroHassinIwama2002].
Graph Partitioning Approaches
At first glance community detection seems close to graph partitioning problems in machine learning. Unfortunately one may not apply available methods for partititioning to the problem of community mining because of the assumptions on availability of predefined partition size, which is not a valid assumption for real social networks.
The objective of graph partitioning algorithms is to divide the vertices of the graph into k groups of predefined size, while minimizing the number of edges lying between these groups, called cut size [Fortunato2010]. Finding the exact solution in graph partitioning is known to be NP-complete.
However there are several fast but sub-optimal heuristics. The most well-known Kernighan-Lin algorithm [KernighanLin1970].
The Kernighan-Lin algorithm optimizes a benefit function Q, which represents the difference between the number of edges inside the groups and the number of edges running between them. It start by partitioning the graph into two groups of equal size and then swaps subset of vertices between these groups to maximize Q. After a series of swaps, it chooses the group with largest Q for partitioning in the next iteration.
This algorithm has time complexity where n is the number of vertices [Fortunato2010].
Another important family of graph partitioning algorithms is the spectral clustering methods [NgJordanWeiss2001]. They divide the network into groups using the eigenvectors of matrices, mostly the Laplacian matrix.
The major incompatibility of these methods is that community structure detection assumes that the networks divided naturally into some partitions and there is no reason that these partitions should be of the same size. In minimum cut methods, often it is necessary to specify both the number and the size of the groups.
If one tries to minimize the cut size without fixing the number of groups, the solution would be grouping all the vertices in one group.
Several alternatives measures have been proposed for the cut size, such as
- Conductance Cut
- Cut size divided by minimum of sum of degrees of vertices in C and outside C
- Ratio Cut
- Cut size divided by minimum of number of vertices in the subgraphs [ChanSchlagZien1993]
- Normalized Cut
- Cut size divided by sum of degrees of vertices in C [ShiMalik2000].
Hierarchical Clustering Approaches
Hierarchical clustering approaches define a similarity measure between vertices and group similar vertices together to discover the natural divisions in a given network.
Hierarchical clustering approaches classify into two major categories:
- agglomerative algorithms
- iteratively merge groups with high similarity
- divisive algorithms
- iteratively remove edges connecting vertices with low similarity.
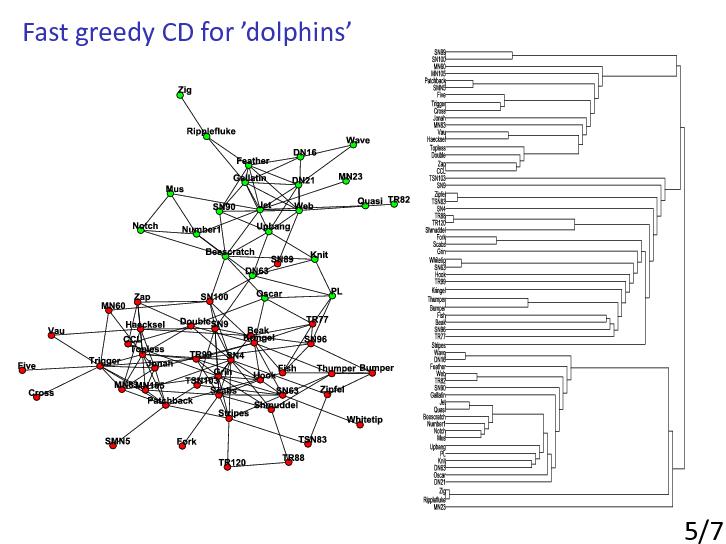
Well-known algorithm that uses hierarchical clustering was proposed by Girvan and Newman [GirvanNewman2002]. Their method is a divisive hierarchical clustering algorithm which iteratively removes the edge with highest betweenness to obtain community structure of the network.
The betweenness of an edge could be computed as the number of shortest paths running through that edge.
High betweenness is a sign for bridges in the network, which are edges connecting different communities.
Their approach obtains a good result in real world data sets, however, it is computationally expensive and unscalable for large networks as it needs running time of O(m2 n) in general and O(n3) in sparse networks, where m is the number of edges [GirvanNewman2002].
Modularity Based Approaches
The modularity Q as defined above is a measure for assessing communities which shows the quality of that particular partitioning of the network.
There are variety of approximate optimization algorithms for searching the space of possible partitionings of a network in order to detect the partitioning with the highest modularity.
Newman uses a greedy optimization in [NewmanGirvan2004]. He employs an agglomerative clustering method, starting with each vertex as a cluster, in each step it merges the clusters that most increase the modularity.
Later Clauset [ClausetNewman2004] presented a very fast version of the algorithm which has become very popular ever since.
A modification of the CNM algorithm [ClausetNewman2004] that treats newly combined communities as a single node after each iteration is able to identify community structure on a network containing 1 billion edges in a matter of hours.
Local algorithms
The more recent directions in community mining includes the investigation of local algorithms for very large networks, the detection of overlapping communities, and the examination of community dynamics.
The idea of LPA (label propagation) algorithm is to assign first each node in a network a unique label (that is all nodes are in different communities). Every iteration, each node is updated in a greedy manner by choosing the label which most of its neighbors have. If there are more than one maximum labels one of such labels is picked randomly. Clear advantage of label propagation is the fact that it can be parallelized easily.
A new fast algorithm is proposed in [BlondelGuillaume2008]. The algorithm is divided in two phases that are repeated iteratively. Assume that we start with a weighted network of N nodes.
- First, we assign a different community to each node of the network.
So, in this initial partition there are as many communities as there are nodes.
- Then, for each node i we consider the neighbors j of i and we evaluate the gain of modularity that would take place by removing i from its community and by placing it in the community of j.
- The node i is then placed in the community for which
this gain is maximum (in case of a tie use a breaking rule), but only if this gain is positive.
- If no positive gain is possible, i stays in its original community.
This process is applied repeatedly and sequentially for all nodes until no further improvement can be achieved and the first phase is then complete.
This first phase stops when a local maxima of the modularity is attained, i.e., when no individual move can improve the modularity.
The first part of the algorithm efficiency results from the fact that the gain in modularity ΔQ obtained by moving an isolated node i into a community C can easily be computed.
The second phase of the algorithm consists in building a new network whose nodes are now the communities found during the first phase.
To do so, the weights of the links between the new nodes are given by the sum of the weight of the links between nodes in the corresponding two communities.
Links between nodes of the same community lead to self-loops for this community in the new network.
Once this second phase is completed, it is then possible to reapply the first phase of the algorithm to the resulting weighted network and to iterate.
Let us denote by «pass» a combination of these two phases. The passes are iterated until there are no more changes and a maximum of modularity is attained.
This simple algorithm has several advantages. First, its steps are easy to implement, and the outcome is unsupervised. Moreover, the algorithm is extremely fast, i.e., computer simulations on large ad-hoc modular networks suggest that its complexity is linear on typical and sparse data.
It was reported that this algorithm has identified communities in a 118 million nodes network in 152 minutes [Fortunato2010].
Clustering
In some way community detection problem in real social networks is related to clustering problem which can be formulated as follows.
Given the set of n points in Rd and an integer k. The goal is to choose k centers from these n points so that to minimize the sum of the squared distances between each point and its closest center.
Social network can be considered as multidimensional space (if each node has a lot of parameters as in Facebook), thus clustering approach may be suitable.
Clustering problem is NP-hard even for k=2 [DrineasFrieze2004].
Very simple local search algorithm was proposed by Lloyd in 1982 [LLoyd1982].
This algorithm is also referred as k-means.
It is good algorithm in terms of speed, but it does not have any proven estimates for its solutions accuracy.
In 2007 [ArthurVassilvitskii2007] enhanced version of Lloyd's algorithm was proposed called k-means++.
It have been proven to be -competitive. Moreover, the algorithm is much faster than k-means and provides better clusterization in practice.
Like k-means this algorithm is fast and can be easily parallelized.
Overlapping communities
Algorithms, described above, produce non-overlapping partitions/communities, and this may be OK in homogeneous social networks, there all connections are professional contacts.
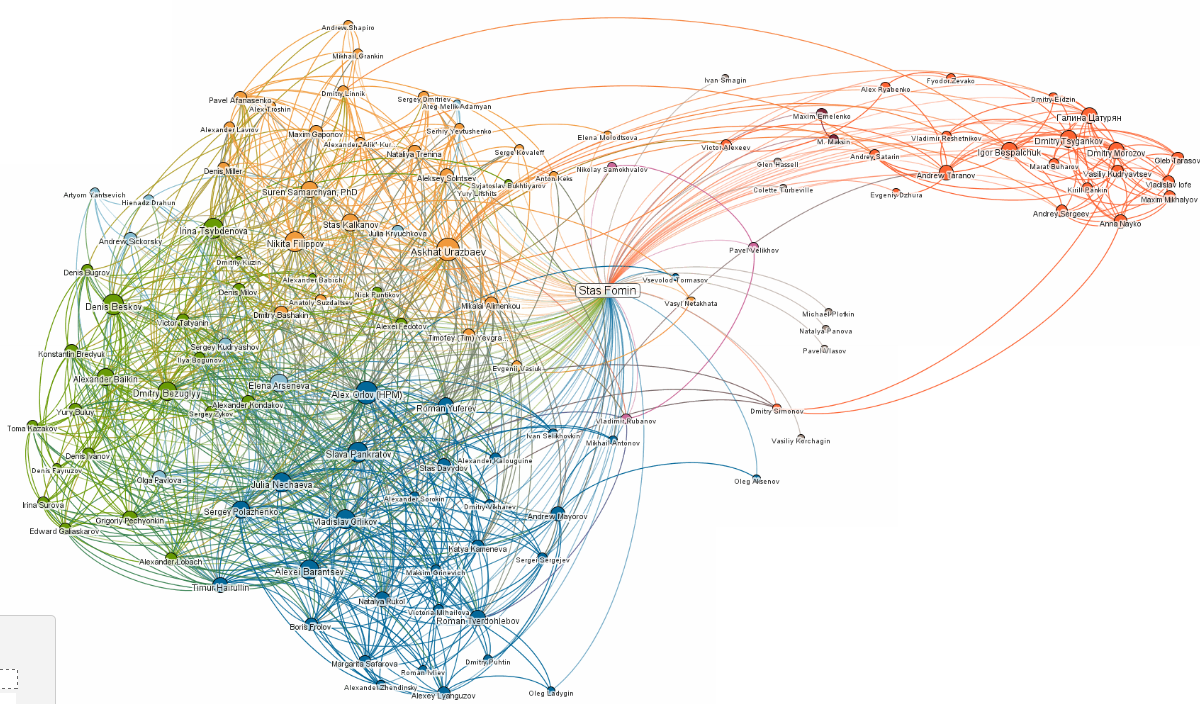
For example, there are good non-overlapping partition of local LinkedIn cluster («professional contacts» of one co-author of the report, forming a «bridge» between several professional communities):
But it is important to note that communities in common social networks (such as Facebook) are often overlapping but all algorithms described above finds only non-overlapping partition of vertices.
For example, none of several «out of box» community detection algorithms (GirvanNewman, Newman-Moore, Louvain, Wakita-Tsurumi) provide reasonable community detection in local Facebook cluster («friends» of one co-author of the report):
The reason of overlapping is based on obvious fact that in social networks all participants share several roles.
So it is desirable, that community detection of social graphs (such as Facebook) will use algorithms for overlapping communities.
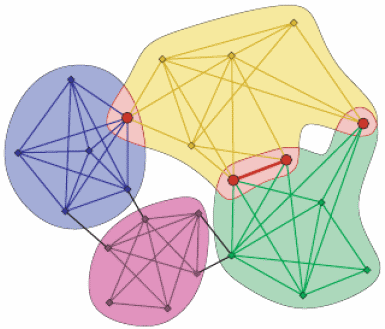
Clique percolation
The clique percolation method ([PallaDerenyiFarkas2005]) builds up the communities from k-cliques. Two k-cliques are considered adjacent if they share k-1 nodes.
A community is defined as the maximal union of k-cliques that can be reached from each other through a series of adjacent k-cliques.
This definition allows overlaps between the communities in a natural way, see picture below.
Since even small networks can contain a vast number of k-cliques, the implementation of this approach is based on locating the maximal cliques rather than the individual k-cliques.
Thus, the complexity of this approach in practice is equivalent to that of the NP-complete maximal clique finding, (in spite that finding k-cliques is polynomial).
This means that although networks with few million nodes have already been analyzed successfully with this approach [PallaBarabasiVicsek2007] no prior estimate can be given for the runtime of the algorithm based simply on the system size.
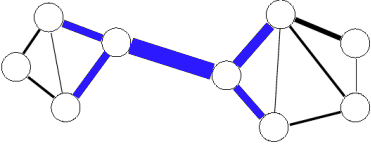
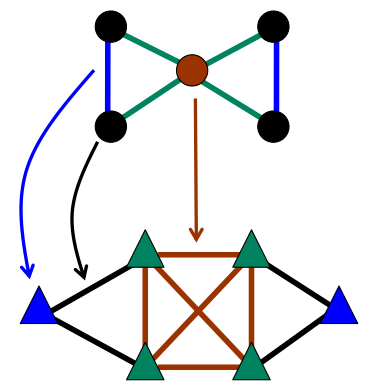
Line graphs
Another new and prominent approach of overlapping community detection is edge partioning (so-called «line graphs») [EvansLambiotte2010].
The algorithm consists of three steps:
- Convert original graph to line graph (see picture), where
- each edge became a vertex in a line graph
- each vertice became a set of edges in a clique.
- Run some classical vertices-partitioning algorithm (may be parallel) on a (weighted) line graph to receive edge separation for original graph.
Conclusions
1. There are different definitions of communities.
It is important to stress that communities in social networks are often overlapping but this fact did not reflected in current definitions of modularity.
This is obvious fact, that in social networks all participants share several roles. So it is desirable, that community detection of social graphs (such as Facebook) use algorithms for non-overlapping communities (clique percolation, partitioning of edge graphs).
2. All community detection algorithms are heuristics.
It is important to have a measure how good approximation the algorithms can provide.
3. In view of very high size of social graphs (expected number of users in Facebook is about billion with average number of connections is 120 [FacebookDataminingSurvey2009]) only very fast heuristics can be considered as candidates mainly using local algorithms.
It seems interesting to apply ideas of good initial choice of k-centers in k-means++ to new fast local algorithms finding communities.
References — community and clustering
- [AlonKrivelevichSudakov1998] N. Alon, M. Krivelevich, B. Sudakov, Finding a large hidden clique in a random graph, Random Structures and Algorithms, 1998, v. 13, pp. 457--466.
- [AsahiroHassinIwama2002] Y. Asahiro, R. Hassin, and K Iwama. Complexity of finding dense subgraphs. Discrete Appl. Math., 121(1-3):15-26, 2002.
- [ArthurVassilvitskii2007] D. Arthur, S. Vassilvitskii. k-means++: the advantages of careful seeding. Proceedings of the eighteenth annual ACM-SIAM symposium on Discrete algorithms, P. 1027-1035, 2007.
- [BackstromHuttenlocher2006] Lars Backstrom, Dan Huttenlocher, Jon Kleinberg, and Xiangyang Lan. Group formation in large social networks: membership, growth, and evolution. In ACM SIGKDD, pages 44-54, 2006.
- [BlondelGuillaume2008] Vincent D. Blondel, Jean-Loup Guillaume, Renaud Lambiotte, Etienne Lefebvre. Journal of Statistical Mechanics: Theory and Experiment, V. 2008(10), 2008.
- [BrandesDellig2006] Brandes U, Delling D, Gaertler M, Goerke R, Hoefer M, Nikoloski Z and Wagner D, On Finding Graph Clusterings with Maximum Modularity, 2006.* [Charikar2000] M. Charikar. Greedy approximation algorithms for finding dense components in a graph. In APPROX, pages 84-95, 2000.
- [ChenZaianeGoebel2009] J. Chen, O. R. Zaiane, and R. Goebel. Local community identification in social networks. In Proceedings of the International Conference on Advances in Social Network Analysis and Mining(ASONAM), pages 237—242, 2009. http://webdocs.cs.ualberta.ca/~zaiane/postscript/SNAkdd10.pdf
- [Clauset2005] A. Clauset. Finding local community structure in networks. Physical Review E, 72:026132, 2005.
- [ClausetNewman2004] A. Clauset, M. E. J. Newman, and C. Moore. Finding community structure in very large networks. Phys. Rev. E, 70:066111, 2004.
- [DrineasFrieze2004] P. Drineas, A. Frieze, R. Kannan, S. Vempala, V. Vinay. Clustering large graphs via the singular value decomposition. Machine Learning, V. 56(1-3), P. 9-33, 2004.
- [EvansLambiotte2010] Evans, TS, Lambiotte R, Line Graphs of Weighted Networks for Overlapping Communities, European Physical Journal B
- [FeigeKortsarzPeleg1997] U. Feige, G. Kortsarz, and D. Peleg. The dense k-subgraph problem. Algorithmica, 29:410-421, 1997.
- [FlakeLawrenceGiles2000] G.W. Flake, S. Lawrence, and C. L. Giles. Efficient identification of web communities. In KDD, pages 150—160, 2000.
- [Fortunato2010] Santo Fortunato. Community detection in graphs. Physics Reports, 486(3-5):75 — 174, 2010.
- [FacebookDataminingSurvey2009] Maintained Relationships on Facebook, Report 2009, http://www.facebook.com/note.php?note_id=55257228858&ref=mf
- [Goldberg1984] A. V. Goldberg. Finding a maximum density subgraph. Technical report, 1984.
- [Hastad97] J. Hastad, Some optimal inapproximability results, STOC’97, Proc. of the 29th Annu. ACM Symposium on Theory of Computing.
- [Hastad1997] J. Hastad, Clique is hard to approximate within $n^{1-\varepsilon}$, Proceedings of the 37th Annual IEEE Symposium on Foundations of Computing, 1997, pp. 627-636.
- [JuelsPeinado1998] A. Juels, M. Peinado, Hiding Cliques for Cryptographic Security, Proceedings of the 9th Annual ACM-SIAM Symposium on Discrete Algorithms, 1998, pp. 678-684.
- [GirvanNewman2002] Michelle Girvan and M. E. J. Newman. Community structure in social and biological networks. In Proceedings of the National Academy of Science USA, 99:8271-8276, 2002.
- [Gregory2007] S. Gregory. An algorithm to find overlapping community structure in networks. In PKDD, pages 91-102, 2007.
- [KernighanLin1970] B. W. Kernighan and S. Lin. An efficient heuristic procedure for partitioning graphs. Bell System Technical Journal, 9:291-307, 1970.
- [LuoWangPromislow2006] F. Luo, J. Z. Wang, and E. Promislow. Exploring local community structures in large networks. In WI ’06: Proceedings of the 2006 IEEE/WIC/ACM International Conference on Web Intelligence, pages 233—239, 2006.
- [LLoyd1982] Stuart P. Lloyd. Least squares quantization in PCM. IEEE Transactions on Information Theory, V 28(2), P. 129-136, 1982.
- [NepuszPetrocziNegyessy2008] T. Nepusz, A. Petroczi, L. Negyessy, and F. Bazso. Fuzzy communities and the concept of bridgeness in complex networks. Physical Review E, 77, 2008.
- [Newman2004] M. E. J. Newman. Detecting community structure in networks. Eur. Phys. J.B, 38:321-330, 2004.
- [Newman2006] M. E. J. Newman. Modularity and community structure in networks. PROC.NATL.ACAD.SCI.USA, 103, 2006.
- [NewmanGirvan2004] M. E. J. Newman and M. Girvan. Finding and evaluating community structure in networks. Physical Review E, 69, 2004.
- [NgJordanWeiss2001] A. Ng, M. Jordan, and Y. Weiss. On spectral clustering: Analysis and an algorithm. In NIPS, pages 849—856, 2001.
- [PallaDerenyiFarkas2005] G. Palla, I. Derenyi, I. Farkas, and T. Vicsek. Uncovering the overlapping community structure of complex networks in nature and society. Nature, 435:814-818, 2005.
- [PallaBarabasiVicsek2007] G. Palla, A.-L. Barabási and T. Vicsek, Quantifying social group evolution, Nature, 446, 664–667(2007).

[ Хронологический вид ]Комментарии
Войдите, чтобы комментировать.