Открытые бизнес-задачи

Материал из DISCOPAL
Перейти к: навигация, поиск

Всего страниц найдено: 45.

----


Проект годовой отчетности компании 2023-12-24 03-10-23 image0.png

В таблице перечислены виды деятельности, связанные с составлением годовой отчетности компании (с указанием их продолжительности в днях и зависимостей)

Код | Деятельность | Продолжительность | Зависит от A | Инвентаризация (физический подсчет) | 2 | B | Оценка товарно-материальных запасов (пересчет в функциональную валюту)| 0.25 | A C | Ваучеры (идентификация счетов-фактур) | 2 | D | Бухгалтерские записи | 1 | C E | Аудит I (проверка остатков) | 1 | D F | Аудит II (обзор процесса регистрации) | 0.5 | E G | Обращение текущих счетов дебиторов | 7 | D H | Обращение текущих счетов (долевые активы) | 5 | F I | Окончательная проверка балансовых остатков | 3 | FG J | Судебный баланс | 0.5 | I K | Регуляризация (определение бухгалтерского результата) | 0.5 | G L | Окончательный баланс | 0.5 | JK

  • Постройте граф проекта
  • Постройте критические пути, посчитайте время


Проект киносьемки 2023-12-24 02-16-18 image0.png

В следующей таблице перечислены мероприятия, на которые делится кинопроект, их продолжительность в днях и зависимости предшествования.

Код | Суть работы | Зависит | Длительность 

a  |  Написать сценарий                      |          |   30
b  |  Найти местность для сьемки на воздухе  | a        |   10
c  |  Получить у местных властей разрешение  | b        |  
d  |  Подбор интерьеров для внутренних сьемок| a        |    8
e  |  Кастинг актеров                        | a        |   10
f  |  Нанять технический персоналa           | a        |    8
g  |  Размещение актеров и техперсонала      | ef       |    1
h  |  Костюмы                                | e        |    5
i  | Съемка на местности без актеров         | cf       |    1
j  | Съемки с актерами                       | ihgd     |

  • Визуализируйте граф работ
  • Найдите критические пути и ожидаемую продолжительность проекта.


Сыроварня 2023-12-24 02-07-02 image0.png

Сыроварня производит три вида сыра: зрелый сыр, полутвердый сыр и свежий сыр. Используется два вида молока: овечье и козье. Завод оснащен двумя типами машин.

  • Машина 1 использует 70 литров овечьего молока и 200 литров козьего молока в час для производства 9 килограммов зрелого сыра, 2 килограммов полутвердого сыра и 5 килограммов свежего сыра.
  • С помощью машины 2 каждый час получается 10, 5 и 4 килограмма каждого сыра соответственно при расходе 100 литров овечьего и 80 литров козьего молока.

Учитывая исследования спроса на три вида продукции, компания считает, что должна производить не менее 900 и 300 килограммов плавленого и полуплавленого сыра в день соответственно, и не более 800 килограммов свежего сыра.

Прибыль на килограмм каждого вида сыра составляет 4, 6 и 7 евро соответственно.

Руководство компании поставило перед собой следующие цели и задачи с указанием приоритетов:

  • Приоритет 1. Количество молока, используемого для производства сыра, не превышает 14000 литров в день для овечьего молока и 20 000 литров в день для козьего молока.
  • Приоритет 2. Количество козьего молока не превышает количество овечьего молока.
  • Приоритет 3. Максимизация выгоды. Смоделируйте и решите задачу, чтобы рассчитать количество часов в день, в течение которых должны работать машины.

Рассчитать количество часов в день, в течение которых должны работать машины.


Найм временного работника 2023-12-24 01-54-15 image0.png

Компания хочет заполнить вакансию временным персоналом на ближайшие 4 месяца.

Для этого она пользуется услугами агентства по временному трудоустройству, которое берет 200 евро за каждого нанятого сотрудника.

В первый месяц компания нанимает одного человека, а в начале последующих месяцев решает, нанимать ли нового человека или продолжить работу с ранее нанятым.

Известно, что зарплата за первый отработанный месяц составляет 900 евро, а прибыль, полученная компанией, - 2000 евро.

Во второй отработанный месяц сотрудник будет иметь зарплату 1000 евро, обеспечивая прибыль в 2100. Если сотрудник проработает три месяца или больше, то его зарплата составит 1100 в третьем месяце и 1200 в четвертом, что обеспечит прибыль в 2200 и 2300 за третий и четвертый месяц соответственно.

Кроме того, известно, что агентство временного трудоустройства по окончании контракта с работником, проработавшим 1, 2, 3 или 4 месяца, должно выплатить ему 100, 200, 300 или 650 евро соответственно.

Рассчитайте политику найма персонала месяца, которая принесет наибольшую выгоду компании, на ближайшие 3 и 4 месяца.


Прокладка водопровода в селе 2023-12-24 01-26-35 image0.png

Муниципалитет хочет разработать способ доставки воды из муниципального водохранилища «D» в 7 сельских домов, не обязательно напрямую, с наименьшими возможными затратами.

Возможные варианты трубопроводов между водохранилищем и домами с соответствующими затратами в

денежных единицах приведены в следующей таблице (приведен только верхний треугольник симметричной матрицы):

. D C1 C2 C3 C4 C5 C6 C7 D x 10 12 14 x x x x C1 x x x x 3 x x x C2 x x x x 2 4 x x C3 x x x x x 3 x x C4 x x x x x 3 5 6 C5 x x x x x x 7 5 C6 x x x x x x x 4 C7 x x x x x x x x

Например, проезд между 2-м и 5-м домами стоит 4 денежные единицы.

Рассчитайте все возможные способы соединения так, чтобы общая стоимость была минимальной.

(визуализируйте графы).


Выход на рынок запчастей 2023-12-24 01-17-11 image0.png

Автомобильная компания производит изделие, предназначенное для рынка «оригинального оборудования» (что ставят в новые автомобили), удельная прибыль которого составляет $K.

Компания рассматривает возможность вывода своего изделия на рынок «запасных частей», поскольку на этом рынке удельная

прибыль ее продукта удваивается. Руководство компании не планирует увеличивать свои текущие производственные мощности, которые составляют максимум 800 штук в день.

Сценарий 1

В качестве первого подхода к этому рынку и опасаясь потерять текущую клиентскую базу, руководство компании приняло решение ежедневно направлять не менее 75% общего объема производства на рынок «оригинального оборудования» и не менее 160 единиц на рынок «запасных частей».

Определите, ежедневное количество товара, которое должно быть распределено на каждом из двух рынков с целью максимизации прибыли и распределения как можно большего количества товаров на рынке «первой команды».


Сценарий 2

Потенциальный клиент, работающий на рынке «запасных частей», представил руководству компании заказ на 180 единиц продукции в день. Руководство компании решило переосмыслить сложившуюся ситуацию, поставив перед собой следующие цели и задачи в следующем порядке:

  • Приоритет 1. Количество предметов, ежедневно предназначенных для «первого оборудования», составляет не менее 75% от общего объема производства.
  • Приоритет 2. Количество «запасных частей» в день достаточно для удовлетворения потребностей нового клиента.
  • Приоритет 3. Количество изделий, ежедневно предназначенных для «запасных частей», не превышает 20% от общего объема производства.
  • Приоритет 4. Максимальная выгода.

Определите ежедневную сумму, которую следует выделить на каждый из двух рынков.


На следующем графе показана проектная деятельность, с оптимистичным, наиболее вероятным, и пессимистичным временем в днях:

Граф проекта, PERT-анализ 2023-12-24 00-51-47 image0.png
  • Определите предполагаемую среднюю продолжительность проекта, отклонение продолжительности проекта и критические виды деятельности.
  • Составьте таблицу работ.

Получите моделированием ответы на вопросы:

  • На сколько дней можно сократить среднюю продолжительность работ C, чтобы средняя продолжительность проекта сократилась на ту же величину?
  • Если к первоначальному проекту добавляется новое мероприятие G, непосредственным предшественником которого является E, то сколько дней (в среднем) оно должно длиться, чтобы средняя продолжительность проекта, рассчитанная в пункте a), осталась неизменной?
  • Если новому виду деятельности G непосредственно предшествуют E и D, то сколько дней (в среднем) он должен длиться, чтобы средняя продолжительность проекта, рассчитанная в выше, осталась неизменной?


Распределение летних отпусков 2023-12-23 23-46-20 image0.png

Менеджер по персоналу компании хочет распределить летние отпуска трех человек, входящих в его отдел. Отпуска берутся на календарный месяц целиком.

Для того чтобы распределить отпуск наилучшим образом, он решил составить список предпочтений на июнь,

июль, август и сентябрь, как показано в следующей таблице:

. Июнь Июль Август Сентябрь P1 5 4 9 x P2 x 3 6 7 P3 7 5 5 6

И решил отправлять в отпуск максимизируя сумму предпочтений

В этом году директор по персоналу решил привлечь четвертого сотрудника из другого отдела в свой отдел на летние месяцы, чтобы покрыть минимальные потребности своего отдела.

Вариант2.

Рассчитайте распределение, которое оптимизирует уровень предпочтений, если предпочтения четвертого человека были такими:

. Июнь Июль Август P4 6 x 9

Учитывая, что четыре человека должны взять отпуск в июне, июле, августе (каждый по целому месяцу) и что в каждом из этих трех месяцев, должен быть хотя бы один человек в отпуске.

Вариант1.

Найдя четвертого сотрудника, P4, единственным предпочтением которого является постоянная работа в отделе в течение

трех из четырех месяцев, директор по персоналу считает, что неплохо было бы включить сентябрь в планирование. Рассчитайте отпуски, оптимизирующее уровень предпочтений всех четырех человек, если все четверо будут брать отпуск во все четыре месяца и каждый в свой месяц.


Аэроперелет для туристов 2023-12-23 23-23-19 image0.png

Туристическое агентство планирует пакетный отдых в туристическом направлении C. Есть два аэропорта вылета: A1 и A2. Прямых рейсов нет.

Возможные стыковочные аэропорты: B1, B2, B3, B4 и B5.

Места в эконом-классе, доступные на рейсах между аэропортами, где есть достаточно времени

для пересадок, представлены в таблице ниже:

. B1 B2 B3 B4 B5 C A1 45 20 25 x x x A2 x x 30 x x x B1 x x x 20 25 x B2 x x x 20 x x B3 x x x x 35 20 B4 x x x x x 40 B5 x x x x x 60

  • Визуализируйте граф отправки туристов в С.
  • Сколько максимально туристов можно отправить?


Три изделия на двух из четырех станков 2023-12-23 23-15-17 image0.png

Предприниматель, производящий три изделия P1, P2, P3, хочет найти дневной объем производства, который позволит ему максимизировать прибыль.

  • Эти изделия обрабатываются на двух из четырех имеющихся в его распоряжении станков, либо A и B, либо C и D.
  • Количество часов работы каждой машины составляет 190, 210, 170 и 200 соответственно.
  • Постоянные дневные затраты на запуск каждого из этих станков составляют 20, 25, 35 и 15 денежных единиц соответственно.
  • Доход от этих изделий составляет 5 денежных единиц на единицу изделия P1, 5 денежных единиц на единицу изделия P2 и 10 денежных единиц на единицу изделия P3.
  • На каждую единицу станка и изделия необходимо затратить следующие часы:

. A B C D P1 1 1 2 1 P2 1 1 1 2 P3 2 1 1 1

  • Максимизируйте общую дневную прибыль.

Вариация:

  • Добавьте ограничение, что при производстве товара P1 должно быть произведено не менее 10 единиц и не более 20 единиц товара P2 и не менее 5 единиц товара P1.


Следующая сеть представляет собой проект, а значения, присвоенные каждой дуге, обозначают продолжительность работ в проекте в днях.

Критический путь проекта по графу - 02 2023-12-23 23-02-38 image0.png
  • Определите ожидаемую продолжительность проекта и критический путь, напечатайте таблицу работ с временами начала, окончания, возможностью задержек и т.п.


Разные производственные процессы с одними типами оборудования 2023-12-23 22-28-43 image0.png

Компания использует два различных производственных процесса для производства продукта. Каждый процесс требует использования трех машин M1, M2 и M3. Чтобы произвести одну единицу продукта в соответствии с производственным процессом на каждой из выбранных машин необходимо отработать часы, указанные в таблице ниже:

станки\процесс Процесс1 Процесс2 M1 1 3 M2 4 2 M3 3 4

  • Выручка за единицу продукции, произведенную по процессу «1» — 55 евро, а по процессу «2» — 75 евро.
  • Стоимость машино-часа составляет 5 евро.
  • Каждый станок доступен в течение 60 часов.

Выясните, оптимальное количества единиц продукции, которые необходимо распределить по каждому производственному процессу, максимизируя прибыль.

Рассмотрите варианты с дополнительными политическими ограничениями:

  • Количество часов, отработанных на станках M1 и M2, совпадает.
  • Количество часов, отработанных на станке M3, не более чем в 2 раза превышает количество часов, отработанных на станке M1.


Критический путь для проекта по таблице-03 2023-12-23 21-44-40 image0.png

В таблице указаны работы, продолжительность в днях и непосредственные зависимости.

  • Визуализируйте граф работ по проекту, представляющую проект.
  • Какова продолжительность проекта, если продолжительность работы «D» меньше двух дней?
    • Составьте таблицу работ проекта, указав критические работы.
  • Если работа «D» может быть отложена на ½ дня без изменения продолжительности проекта, то какова продолжительность деятельности D?


Сдача помещения в аренду 2023-12-23 21-41-38 image0.png

Владелец помещения рассматривает вопрос о сроке аренды помещения. В следующей таблице приведены расчеты ожидаемой прибыли в сотнях евро при аренде с начала i-го года до начала j-го года.

i\j 2 3 4 5 1 12 22 38 40 2 x 13 20 29 3 x x 10 19 4 x x x 12

Владелец хочет знать, когда сдавать помещение в аренду и на какой срок, чтобы максимизировать ожидаемую прибыль в течение следующих 4 лет.


Оптимизация двух производственных линий 2023-12-23 21-23-48 image0.png

У компании есть две производственные линии для выпуска одного и того же товара.

  • Линия 1 производит 2 единицы продукции в минуту с прибылью в 3000 евро за единицу,
  • линия 2 производит 3 единицы продукции в минуту с прибылью в 5000 евро за единицу.
  • Стоимость хранения одной единицы составляет 10 евро в минуту.

Рассчитайте еженедельное производственное время, которое должно быть выделено на каждую из цепочек, если компания поставила перед собой следующие цели и задачи со следующим порядком приоритетов.

Рассчитайте еженедельное производственное время, которое должно быть

выделено на каждую из цепочек, если компания поставила перед собой следующие цели и задачи со следующим порядком приоритетов.

Надо максимально увеличить еженедельную прибыль.

Дополнительно, вариантами рассмотрите добавление следующих ограничений:

  • Производить не менее 30 000 единиц продукции в неделю.
  • Требовать, чтобы стоимость хранения не превышает 450000 евро в неделю.
  • Еженедельное время производства на линии «1» не меньше, чем на линии «2», но не более чем в три раза больше.


Реставрация картин 2023-12-23 21-00-31 image0.png

По случаю пятисотлетия со дня рождения знаменитого художника один крупный музей решил отреставрировать пять его работ, наняв три реставрационные бригады. Каждая команда представила бюджет реставрации для каждой из работ, как показано в таблице ниже, в тысячах евро.

(где "x" означает, что такое бригада не возьмется за такую работу).

. Картина1 Картина2 Картина3 Картина4 Картина5 Бригада1 60 x 90 x 120 Бригада2 70 90 80 100 80 Бригада3 x 70 120 90 100

Первая реставрационная группа состоит из шести человек,

вторая — из четырех, третья — из трех. Для восстановления каждой из работ требуется по два человека.

Каждый человек в команде восстанавливает только одну работу.

Первая задача — выполнить пять реставраций с минимально возможной стоимостью,

учитывая, что каждая реставрация должна выполняться одной реставрационной бригадой и что в этих реставрациях должны быть задействованы все три бригады?

Вариация — учитывая, что стоимость реставрации пяти работ очень высока, руководство музея решает отреставрировать только три из них, поручив каждой команде по одной работе.

Определите, все возможные задания, которые минимизируют общую стоимость.


Кондитерская фабрика и производство конфет 2023-12-23 20-44-14 image0.png

Кондитерская фабрика производит два вида конфет C1 и C2.

  • Каждый килограмм конфет C1 продается за 200 евро и содержит 100 г сахара и 200 г фруктов.
  • Каждый килограмм конфет C2 продается за 300 евро, содержит 400 г сахара и 400 г фруктов.
  • Разница между еженедельным производством C1 и C2 составляет не менее 5 кг.
  • Кроме того, еженедельное содержание фруктов должно составлять не менее 1600 г.

Найдите решения:

  • максимизировующие доход
  • минимизирующие содержание сахара в еженедельной продукции.

Проверьте гипотезу, что уменьшение в производстве количества сахара на 1кг эквивалентно увеличению дохода на 2 евро.

Добавим еще стоимость упаковки. Пусть стоимость упаковки конфет составляет 0,1 евро за кг для конфет типа C1 и 0,2 евро за кг для конфет типа C2.

Получите эффективные решения, которое

  • максимизирует еженедельную выручку
  • минимизирует количество сахара, используемого в неделю.
  • минимизирует еженедельные затраты на упаковку.


Производство мыла 2023-12-23 19-37-25 image0.png

Фабрика производит 4 вида мыла, для которых требуется 6 компонентов. В таблице ниже приведены количества, необходимые для изготовления одного бруска каждого вида мыла.

. масло(мл) вода(мл) сода(г) глицерин(г) лимон(мл) клубника(мл) Мыло1 250 240 42 1 1 3 Мыло2 200 210 2 40 2 1 Мыло3 230 240 20 25 3 1 Мыло4 180 200 10 35 1 3

В день на фабрике производится

  • 150 литров масла,
  • 160 литров воды,
  • 12 кг каустической соды,
  • 3 кг глицерина,
  • 2 литра лимонной эссенции
  • 3 литра клубничной эссенции.


  • В день должно производиться не менее одного вида мыла и не более трех.
    • Кроме того, если производится мыло первого типа, то мыло четвертого типа

производить нельзя.

  • Прибыль с одного бруска мыла составляет 10, 13, 15 и 11 евро соответственно для каждого вида мыла.

Максимизируйте прибыль.

Вариация: в будущем, фабрика планирует расширить производственный цех стоимостью 200000 евро, так что в случае расширения наличие компонентов увеличится на 50 литров масла, 70 литров воды, 4 кг каустической соды, 4 кг глицерина, 1 литр лимонной эссенции и 500 мл клубничной эссенции.

Но в случае такого расширения, если будут производиться мыло3, придется также производить мыло1.

Максимизируйте прибыль.


Маршруты для грузовиков 2023-12-23 19-19-58 image0.png

У транспортной компании есть 4 грузовика и 4 маршрута.

Каждый грузовик должен выполнять один маршрут, и каждый маршрут должен выполняться только одним грузовиком.

Прибыль каждого перевозчика на разных маршрутах зависит от характеристик грузовика и выбранного маршрута и

представлена в следующей таблице: 

 .          Маршрут1 Маршрут2 Маршрут3 Маршрут4

Грузовик1 150 200 300 100 Грузовик2 100 220 300 250 Грузовик3 250 140 240 240 Грузовик4 300 250 100 300

По какому маршруту должен двигаться каждый грузовик, чтобы максимизировать общую прибыль?

Вариация: Торговый агент компании выиграл два новых маршрута и хочет опробовать их в этом году. Прибыль, полученная с каждого грузовика, составляет: 

  .        Маршрут5 Маршрут6

Грузовик1 200 260 Грузовик2 300 280 Грузовик3 250 250 Грузовик4 250 320

  • Решите вариант, при условии, что каждый грузовик может проехать только по одному маршруту, а новые маршруты должны быть обязательными.


  • Решите вариант, при условии,
    • все маршруты должны быть пройдены,
    • каждый грузовик может проехать более одного маршрута и все грузовики должны быть использованы.
    • Кроме того, грузовик 1 сможет проехать не более 450 км.
    • В день грузовики 2 и 3 смогут проезжать не более 300 км в день, а грузовик 4 — 160 км в день,
    • маршруты 1, 2, 3, 4, 5, 6 — 110, 150, 130, 150, 120 и 90 км соответственно.


Политика замены оборудования 2023-12-23 18-45-48 image0.png

Компания собирается определить политику замены оборудования на ближайшие 4 года. Стоимость приобретения оборудования в любой год неизменна и составляет $7000.

Год СтоимостьОбслуживания ОстаточнаяСтоимость 1 1000 4000 2 1000 2500 3 2000 2000 4 3000 0

Первая задача:

  • Постройте визуализацию (граф) возможных политик замены.
  • Рассчитайте политику замены которая
    • минимизирует общие чистые затраты (стоимость приобретения + стоимость обслуживания - ликвидационная стоимость), принимая во внимание, что в начале года 1 необходимо приобрести новую единицу оборудования, а в конце периода не требуется никакого оборудования.

Вариация:

  • Повторите предыдущее, с учетом того, что вступает в силу новое законодательство, согласно которому оборудование должно обслуживаться каждые два года, если оно не заменено, по цене 2000 денежных единиц за обслуживание.


Выбор места для завода стиральных машин 2023-12-23 16-38-20 image0.png

Компания, производящая бытовую технику, планирует открыть новый завод по производству 3 моделей стиральных машин: высокого, среднего и эконом-класса.

  • У компании есть два возможных места расположения: 1 и 2.
  • Инвестиции, необходимые для строительства завода в месте 1, составляют 2000000 денежных единиц, а в месте 2 — 1750000 денежных единиц.
  • Удельные издержки производства составляют 15, 13 и 10 денежных единиц соответственно для высокого, среднего и низкого диапазона в месте 1 и 16, 12 и 9 денежных единиц соответственно в месте 2.
  • Ежегодно будет выпускаться не менее 75 000 единиц высшего класса, 100 000 среднего и 200 000 низшего.


  • Первая задача — построить только один завод, смоделируйте задачу с целью минимизации затрат.
  • Вторая задача — если включена возможность строительства двух заводов, (расположение 1 и 2), смоделируйте задачу с целью минимизации затрат, учитывая, кроме того, следующие ограничения:
    • В случае производства стиральных машин низкого класса в месте 1 будет получена субсидия в размере 1000000 денежных единиц.
    • Высококлассная продукция будет производиться только в одном из двух мест.


Критический путь для проекта по таблице-02 2023-12-23 16-27-24 image0.png

В таблице представлен набор работ, составляющих проект, а также их продолжительность в днях и отношения приоритета между ними.

  • Визуализируйте граф работ, и найдите ожидаемую продолжительность проекта.
  • Выведите таблицу проектной деятельности.

Ответьте на следующие вопросы.

  • Что произойдет с продолжительностью проекта, если работа «I» задержится на 2 дня?
  • На сколько дней может быть отложена работа «D» без ущерба для запланированной продолжительности проекта?
  • Сколько времени должна длиться деятельность «B», чтобы она стала критической, если продолжительность других видов деятельности остается неизменной?



Критический путь для проекта по таблице 2023-12-23 15-29-04 image0.png

Проект состоит из 11 видов работ, закодированных латинскими буквами. В таблице перечислены эти работы, их продолжительность в днях и зависимости между ними:


  • Визуализируйте сетевой граф, представляющий этот проект.
  • Зная, что критическими работами проекта являются A, C, D, G, H, I и J, рассчитайте ожидаемую продолжительность

проекта, критические пути и продолжительность работ D и H.

  • Вычислите запас времени для некритичных видов деятельности.


Рассмотрим следующую сеть:

Максимальный поток на графе 2023-12-23 15-19-22 image0.png
  • Если значения каждой дуги представляют собой расстояния, выясните, каким должно быть «a», чтобы кратчайший маршрут от узла 1 до узла 7 обязательно проходил через узел 2.
  • Если значения дуг представляют собой мощности потока, при «a=5», вычислите значение пикового расхода от узла 1 до 7.


Производство хлеба в пекарне 2023-12-23 15-10-48 image0.png

Пекарня хочет ввести производство двух новых видов хлеба: цельнозернового и ржаного, поскольку сбыт их продукции гарантирован.

Эти виды хлеба изготавливаются в основном из трех ингредиентов: цельнозерновых отрубей,

пшеничной и ржаной муки.

  • Для приготовления 1 кг цельнозернового хлеба требуется 350г цельнозерновых отрубей 150 г пшеничной муки, а для приготовления 1 кг ржаного хлеба — 250 г пшеничной и 250 г ржаной муки.
  • Ежедневное наличие цельнозерновых отрубей составляет 210 кг, пшеничной муки — 115 кг, ржаной муки — 100 кг.
  • Прибыль на килограмм цельнозернового хлеба составляет 0,40€, а на килограмм ржаного хлеба — 0,60€.

Рассчитайте суточное производство цельнозернового и ржаного хлеба, если в порядке очередности были поставлены следующие задачи:

  • Приоритет 1. Желательно, чтобы прибыль составляла не менее 240 евро в день.
  • Приоритет 2. Желательно, чтобы количество ежедневно производимого цельнозернового хлеба было как минимум вдвое больше, чем ржаного.
  • Приоритет 3. Желательно, чтобы ежедневное количество производимого ржаного хлеба составляло не менее 300 кг.

Какие из предложенных целей могут быть достигнуты?



Следующая сетка представляет собой проект, где значение каждой дуги указывает на продолжительность каждого вида работ в днях:

Критический путь проекта 2023-12-23 01-45-36 image0.png

Определите, для каких значений «t(1,3)», «t(1,6)» и «t(8,9)» выполняются следующие три условия:

  • Ожидаемая продолжительность проекта - 23 дня.
  • Активность «(2,6)» имеет решающее значение.
  • Дедлайн активности «(3,4)» равен 4.

Затем найдите критический путь (пути) проекта и таблицу работ («самое раннее начало», «дедлайн»).


Реклама в СМИ 2023-12-23 02-28-57 image0.png

Компания по продаже недвижимости хочет продвинуть новый проект с помощью рекламной кампании.

У нее есть 5 видов рекламы:

tvm
реклама на местном телевидении в полдень
tvn
реклама на местном телевидении вечером
per
реклама в местной газете
sup
реклама в местном воскресном приложении
rad
реклама на местном радио утром.

Компания собрала данные о количестве потенциальных клиентов, на которых нацелился каждый вид рекламы, и стоимости каждой рекламы в евро.

Кроме того, была проведена оценка «удельного эффекта» каждого рекламного объявления в зависимости от

носителя, в котором оно демонстрируется, по шкале от 0 до 100 (0 - нет, 100 - отлично).

Данные представлены в следующей таблице:

Канал ПотенциальныхКлиентов СтоимостьЕвро УдельныйЭффект МаксимумОбъявлений tvm 1000 1500 65 15 tvn 2000 3000 90 10 per 1500 400 40 25 sup 2500 1000 60 4 rad 300 100 20 30

Агентство недвижимости, консультируемое рекламным агентством, решает использовать

  • не менее 10 рекламных роликов на ТВ,
  • охватить не менее 50 000 потенциальных клиентов,
  • не тратить более 18000 евро на ТВ-рекламу
  • и, если реклама будет размещена в газете, то не размещать рекламу на ТВ в вечернее время.

Максимальный бюджет рекламной кампании составляет 30 000 евро.

Как следует планировать рекламную кампанию, если максимизировать суммарный эффект (удельный эффект × количество обьявлений) всех объявлений в рекламной кампании.


Группировка людей максимизировать потенциальных лидеров 2023-12-23 02-35-54 image0.png

Пусть имеется группа из n=50 человек, с которыми будет создано m=10 рабочих групп.

Каждая группа будет состоять из фиксированного числа людей. 

1	2	3	4	5	6	7	8	9	10
5	4	4	3	6	4	5	7	6	6

Некоторые люди знают друг друга.

Надо так распределить людей по группам, чтобы максимизировать число людей, у которых в группе все люди, которых они знают.

Беру задачу «Optprob/Игра UnblockMe» себе!


Игра UnblockMe 2022-11-22 02-31-00 image0.png

Опишем игру «Разблокируй меня» (Kira Games 2021) — это игра-головоломка, представляющая собой поле, состоящее из нескольких столбцов и рядов.

  • Блоки располагаются по горизонтально или вертикально;
  • Горизонтальный блок может двигаться только вправо и влево;
  • Вертикальный блок может двигаться только вверх и вниз.
  • Вы должны переместить их таким образом, чтобы освободить путь для красного блока.
  • Количество рядов NF=6
  • Количество столбцов равно NС=6.
  • В этих рядах и столбцах размещается ряд блоков, которые мы будем называть препятствиями, и которые могут быть горизонтальными или вертикальными.
  • Горизонтальные блоки размещаются в ряд и могут быть перемещены только в пределах этого ряда (перемещение вправо и влево).
  • Вертикальные препятствия могут перемещаться только в пределах столбца, к которому они относятся (перемещение вверх и вниз).

С другой стороны, у нас есть красный блок; это горизонтальный блок, расположенный в определенном ряду (ряд 3 на оригинальной игровой панели) и поэтому перемещается только по горизонтали.

В конце этого ряда на доске есть выход.

Наша задача — убрать красный блок с доски.

Мы должны переместить препятствия таким образом, чтобы освободить путь для красного блока.

Мы создадим модель, математически представляющую игру с двумя сценариями:

  • Сценарий, в котором в качестве условия навязывается требование убрать красную фишку с доски. доски. В этом сценарии цель не ставится. Получение выполнимого решения будет означает, что красная фишка ушла с доски.
  • Второй сценарий, как полная оптимизационная задача, в которой целью является достать красную фишку за наименьшее количество шагов (движений).

Не готово, нужно дорабатывать

Беру задачу «Optprob/Размещение городских велостанций» себе!


Размещение городских велостанций 2023-12-23 05-21-10 image0.png

В городе, поделенном на 10 секторов, будут установлены велосипедные станции.

Каждый сектор, имеет определенное количество потенциальных клиентов:

Sectors 1 2 3 4 5 6 7 8 9 10
C 400 300 200 500 350 450 150 250 380 290

В городе есть 40 возможных мест города для установки станций.

Каждое место

  • относятся сектору города
  • позволяет установить станцию и определенное количество креплений для велосипедов до максимального числа креплений, известного для каждого места, в зависимости от его размера.


Место 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40
Максимум велокреплений 30 20 40 45 50 25 15 18 25 25 40 40 45 50 25 15 18 25 25 40 40 45 50 25 15 18 25 25 40 40 45 50 25 15 18 25 25 40 40 30
Сектор 1 2 3 4 5 1 2 3 4 5 6 7 8 9 10 1 2 3 4 5 1 7 8 1 10 9 8 7 7 5 6 4 3 2 1 2 3 4 5 6

Нам известны расстояния между локациями.

Установка станции включает в себя стоимость управляющего компьютера, CO=1200, и стоимость каждого умного крепления (якорной стоянки), каждая из которых оценивается в CB=450.

С другой стороны, необходимо будет также приобрести велосипеды.

Стоимость каждого велосипеда составляет CK=350.

Если будет закуплено более 500 велосипедов, поставщик велосипедов

предлагает скидку в размере Dt=30 за каждый велосипед.

Требования к установке следующие.

  • Во всех секторах должно быть несколько станций.
  • Расстояние между двумя местами со станцией должно быть не менее 300 м.
  • Любое место со станцией должно иметь по крайней мере одно другое место со станцией, расположенной на расстоянии не более 500 м, чтобы избежать длительных поездок при отсутствии велосипедов или свободных стоянок при поездке на станцию.
  • В старом секторе города (сектор 1) может быть установлено не более четырех станций.
  • Количество приобретенных велосипедов должно составлять не менее 70% от общего количества установленных креплений.
  • Если станция устанавливается в каком-либо месте, то количество креплений-якорей должно быть от 8 до его максимальной вместимости.
  • У городского отдела планирования есть бюджет в размере P=9000000 на проект установки.


Задача состоит в том, чтобы сбалансировать соотношение между потенциальными клиентами (чтобы было пропорционально…) и установленными в секторе креплениями.

Беру задачу «Optprob/Производство металлических прутков» себе!


Производство металлических прутков 2023-12-23 04-55-31 image0.png

Есть металлургическая фабрика, на которой производятся металлические пруты, на складе их ( j = 1 … n), n=50. Каждый прут j имеет длину LA_j (в сантиметрах, запятая там для красоты).


Получен заказ на набора запрошенных прутков десяти типов (i = 1...m, m=10). Каждый тип i имеет длину ld_i и количество брусков D_i.

DemandedBars
IdLengthNumber
11,2004
260020
350013
41,5002
52,0005
67005
79005
84005
91,00016
101,10014

На рынке не востребованы бруски длиной менее 200 см, поэтому мы хотим минимизировать общую длину избыточных кусков менее 2 м, т.е. минимизировать отходы. Мы также добавим «стоимость» (размерность в сантиметрах прута) C=200 для каждого используемого складского бруса, чтобы не использовать слишком много складских брусьев.

Т.е. пусть целевая функция 

   \sum_j d_j + C \times \alpha_j

  • где d_j — остаток прута j меньше 200см
  • \alpha_j — индикатор, что прут j вообще использовали.

рассмотреть вариант

  • минимизировать количество используемых складских брусьев
  • запрет на использование кусков размером менее 2 м

Есть не совсем корректное решение (которое можно доделать):

Беру задачу «Optprob/Планирование экскурсий» себе!


Планирование экскурсий 2023-12-23 04-13-02 image0.png

У нас есть группа из 60 экскурсантов, которые наняли услуги компании автобусных туров на следующие 3 дня.

  • Есть шесть различных экскурсий, которые могут быть проведены.
  • Каждый экскурсант выбрал максимум три экскурсии. Экскурсант может взять только одну экскурсию в день.

Вот, какие экскурсии выбрал каждый экскурсант:


  • Автобусы компании имеют вместимость (количество мест). У компании 5 автобусов.
Buses 1 2 3 4 5

60 50 60 60 40

Один автобус в день может совершить несколько экскурсий в зависимости от близости между ними.

Эта информация будет собрана в бинарном атрибуте между экскурсиями (1: они могут быть

выполняться одним и тем же автобусом, 0: нет).

Вблизи 1 2 3 4 5 6
1 0 1 0 0 0 1
2 0 0 0 1 1 0
3 0 0 0 0 1 0
4 0 0 0 0 1 0
5 0 0 0 0 0 0
6 0 0 0 0 0 0
  • Однако автобус не должен охватывать более двух экскурсий за один день.
  • Компания хочет спланировать экскурсии на 3 дня, чтобы использовать наименьшее количество автобусов

(минимизируем «автобусо-дни»).

    • При этом нужно найти назначение экскурсий и экскурсантов на рейсы автобусов

Беру задачу «Optprob/Охрана аптек» себе!


Охрана аптек 2023-12-23 03-41-58 image0.png

В данном городе имеется 52 аптеки, распределенные по 5 районам (j = 1. . .5).

Аптеки бывают двух типов:

  • Обычные (0): Открытие и закрытие в обычные часы, не работают в выходные.
  • Аптеки 12 ч (1): Открыты каждый день в году до 22:00.
Аптека 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52
Тип 1 1 1 1 1 1 1 1 0 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1 1 0 1 1 1 0 1 1 1 1 1 1 1 0 1 1 1 1 1 0 1 1 1 1 1 1
Район 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2 3 3 3 3 3 3 3 3 3 3 3 4 4 4 4 4 4 4 5 5 5 5 5 5 5 5 5 5

Есть годовой календарь праздничных дней:

Когда аптеки не работают, их надо охранять, наркоманы не дремлют.

Вооруженных охранников аптеки нанять не могут, их выделяет муниципалитет.

Существует два типа охранников:

  • Дневной: 9:00-21:00, для выходных-праздничных дней — работают только днем, в выходные.
  • Ночной: 21:00-9:00, работают каждый день.

Но к каждой аптеке охранника не приставить, их не хватает на всех, и хотелось бы как-то более-менее справедливо их распределить.

Район 1 2 3 4 5
Дневных охранников 2 2 1 1 2
Ночных охранников 2 1 1 1 1


Есть куча законодательных еврорегуляций, как их справедливо распределить их по охраняемым объектам.

  • Обычная аптека не может охраняться более 24 часов подряд.
  • Любая аптека не может охраняться два выходных подряд.
  • Разница в ежемесячном количестве караулов в каждой обычной аптеке не может быть быть больше трех.
  • Разница в общем числе караулов всех охранников в для каждой аптеки не превышает двух единиц.

Округи ревниво следят за «Y_j» — количеством ночных охранников аптек, деленное на количество аптек в его округе «j».

Надо минимизировать разницу между «Y_j», соблюдая вышеуказанные регуляции.

Не готово, проблемы с решением

Беру задачу «Optprob/Задача Штейнера о минимальном дереве» себе!


Задача Штейнера о минимальном дереве.

Т.е. у нас есть неориентированный граф, где

  • N=74 узлов, узлы графа двух типов:
Терминальные
Они должны быть частью сети.
Штейнера
Не обязательно, чтобы они были частью сети.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74
Терминальный? 0 0 0 0 0 0 0 0 0 1 1 1 0 1 0 0 0 1 0 0 0 1 0 0 0 0 1 0 1 1 0 0 1 0 0 1 1 1 0 0 0 0 0 0 1 1 1 1 0 0 1 0 0 0 1 0 1 0 1 0 0 0 0 1 0 1 0 0 0 0 0 0 0 0
  • M=153 неориентированных ребер в весом-стоимостью, которых мы представим 306 двойными дугами, ребро (i, j, w) → в ребро i→j (w) и ребро j→i (w)

Надо найти подграф минимальной стоимости, соединающий все терминальные узлы.

Беру задачу «Optprob/Производство штучных изделий» себе!


Производство штучных изделий 2023-12-23 05-14-04 image0.png

Представим некую систему штучного производства.

Есть шесть станков и неопределенное количество операторов.

Каждый станок i имеет производительность R_i единиц продукции в час. 

R_i = 500 300 190 160 100 90
  • К станкам можно приставлять оператора, но это стоит денег.
    • Стоимость оператора за день!
C_i = 150 100 130 120 100 100


  • Станок 4 глючит, если он используется, к нему обязательно приставлять оператора.
  • К остальным станкам оператора не обязательно приставлять, но если приставить — производство ускорится на 20%. Ну или просто можно считать что там будет «увеличенная производительность» заданная 
RR_i = 600 360 228 160 120 108
  • Ни в коем случае нельзя назначать более одного оператора.
  • Если станок работает больше 8 часов, надо заплатить штраф F=1500
  • Надо произвести Q=10000 деталей

Как распределить производство и операторов по станкам, чтобы произвести все, и подешевле?

Есть набросок решения:

📹 видео 📹

Но оно некорректно — предложенное решение — нелинейная ЦЛП (ранее решалась умным солвером), но cbc честно показал что задача — нелинейная ЦЛП, так что ура, ее можно перевести в открытую-нерешенную, и подумать, как сформулировать линейную ЦЛП. Можно взять текущее недорешение как набросок, или подумать с чистого листа.

Беру задачу «Optprob/Управление Дисциплинами» себе!


Управление Дисциплинами 2023-12-23 13-11-56 image0.png

Пусть имеется группа из n=20 человек, с которыми мы собираемся создать m=5 рабочих групп. (эксперты-политики создающие новые законы, ученые, инженеры и т.п.).

У нас есть 10 дисциплин-предметов (научные дисциплины, технологии, законы, …), а насколько каждый человек хорош в каждой дисциплине, задается индексом компетентности ([0…1]),

и все это формирует матрицу

Каждая группа имеет ограничение на минимум и максимум людей

Группа 1 2 3 4 5 Минимум 2 2 5 3 5 Максимум 7 8 7 6 10

  • В каждой группе нужно работать над двумя предметами.
  • Каждый предмет, должен изучаться по крайней мере в одной группе
  • Каждый человек может входить максимум в три группы, но тогда эти у этих групп не должно быть общего предмета.
  • Если индекс компетентности кого-то в предмете меньше 0.5, он не может входить в рабочую группу, которая этим занимается.
  • Предметы, которые изучает группа, должны быть совместимы («нет конфликта интересов», «техника безопасности» … )


Цель формирования групп — максимизировать общую компетентность — сумма индивидуальных компетентностей тех, кто в группе, по дисциплинам, изучаемым в группе — и так по всем группам.

Беру задачу «Optprob/Назначение предметов на аудитории» себе!


Назначение предметов на аудитории 2023-12-23 03-23-35 image0.png

В университете «Синергия» собираемся ежедневноЧтобы упростить размер модели, мы рассматриваем один день преподавания предмета преподавать 150 предметов.

У каждого предмета есть количество учеников.

Расписание предметов уже составлено (как было удобно лекторам), и чтобы не возится с временами начала-окончания, получим сразу важные для нас данные — какой предмет пересекается по времени с каким (не может быть одновременно).

Аудитории мы арендуем в огромном бизнес-центре (неисчерпаемом, «Бесконечный Замок»©), где есть аудитории двух размеров

  • Большие, на 100 человек, стоимость $25 в день
  • Малые, на 50 человек, стоимость $10 в день.

Стоимость аренды в день — т.е. можно в каждую аудиторию внести все «непересекающиеся» занятия (день тоже «растяжимый»).

В большие точно должны влезть группы студентов по любому предмету, в маленькие — не факт.

Сколько и каких комнат арендовать, и как назначить предметы на эти аудитории, чтобы было подешевле и все студенты поместились?

Беру задачу «Optprob/Выбор внеклассных мероприятий» себе!


Выбор внеклассных мероприятий 2023-12-23 02-51-24 image0.png

Школа хочет спланировать распределение внеклассных занятий среди учащихся. Предлагаются следующие виды деятельности (8 активностей, 12 групп):

  • Гимнастика (две группы)
  • Музыка (одна группа)
  • Баскетбол (две группы)
  • Ремесла (одна группа)
  • Рисование (одна группа)
  • Английский язык (две группы)
  • Французский язык (одна группа)
  • Футбол (две группы)

Отображение групп на активности 

 A_k = 1 1 2 3 3 4 5 6 6 7 8 8

Максимум учеников в каждой группе: 

 M = 10 10 10 10 10 10 10 10 10 10 12 12

100 учеников уже запросили различные активности, не зная о расписании:

Занятия проводятся в течение 1 часа

  • в понедельник, вторник, среду и четверг.
  • в слоты «с 4 до 5 часов», «с 5 до 6» или «с 6 до 7 часов» пополудни — 3 слота в день, всего 12 слотов (h).

Для моделирование конкретное время неважно, т.е. есть 4 дня, и 12 часовых слотов, которые так отражаются на дни: 

 D_h = 1 1 1 2 2 2 3 3 3 4 4 4

Расписание занятий уже фиксировано, матрицей 12×12. 

P_kh=1 0 0 0 0 0 1 0 0 0 0 0
     0 1 0 0 0 0 0 1 0 0 0 0
     0 0 1 0 0 0 0 0 1 0 0 0
     0 0 0 1 0 0 0 0 0 1 0 0
     0 0 0 0 1 0 0 0 0 0 1 0
     0 0 0 0 0 1 0 0 0 0 0 1
     1 0 0 0 1 0 0 0 0 1 0 0
     0 1 0 0 0 1 0 0 0 0 1 0
     0 0 1 0 0 0 1 0 0 0 0 1
     0 0 1 0 0 0 1 0 0 0 0 0
     0 0 1 0 0 0 1 0 0 1 0 0
     0 0 0 0 1 0 0 0 0 0 1 0

Есть мероприятия с двумя группами. У каждой группы свое расписание и свое максимальное количество студентов.

Мы собираемся распределить группы мероприятий ученикам с целью максимизации суммы мероприятий, которые

назначены общему числу студентов, принимая во внимание, что:

  • Ученик не может быть назначен в две группы с перекрывающимися видами деятельности.
  • Ученику могут быть назначены только те виды деятельности, которые он запросил.
  • Ученик не может заниматься более чем двумя видами активности в один день.
  • Мы не можем назначить ученика в более чем одну группу по одной и той же активности.

Беру задачу «Optprob/Назначение задач операторам» себе!



Система имеет N=25 задач и M=10 операторов.

Каждая задача имеет следующие характеристики:

  • Приоритет задачи: Значение от 0 до 10.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
Приоритет 4 8 9 9 10 2 3 4 7 7 7 5 5 3 2 2 1 1 1 2 1 1 2 3 4
Назначение задач операторам 2023-12-23 03-11-04 image0.png
  • Время обработки задачи каждым оператором.


1 2 3 4 5 6 7 8 9 10
1 10 0 23 18 19 12 0 0 32 25
2 0 14 0 0 0 4 0 0 5 0
3 0 7 0 0 15 19 0 0 9 0
4 0 0 13 0 0 13 0 0 0 0
5 23 0 0 34 12 15 0 0 45 13
6 0 0 15 13 45 0 35 0 0 0
7 12 15 0 0 45 0 15 0 22 12
8 0 0 0 35 13 13 19 0 10 0
9 0 0 12 0 25 0 25 0 0 0
10 0 24 0 34 12 0 72 0 0 0
11 0 35 0 0 19 0 19 0 0 21
12 23 24 0 34 0 19 0 19 0 0
13 14 35 0 13 0 0 19 13 0 0
14 18 19 0 12 0 72 0 21 0 23
15 14 35 0 0 19 0 0 25 0 0
16 0 24 0 34 0 12 0 72 0 0
17 0 0 13 0 0 0 0 25 0 25
18 0 24 0 0 0 0 0 72 0 21
19 20 14 35 13 13 19 39 0 25 0
20 0 0 0 0 0 13 0 0 20 21
21 0 22 0 0 35 0 0 0 13 0
22 12 13 0 35 0 0 19 0 19 15
23 11 0 35 0 0 0 39 0 12 13
24 10 0 0 35 13 0 19 0 11 12
25 19 0 0 0 0 0 25 0 25 19

Каждый оператор имеет следующие характеристики:

  • Совместимость с задачами: Есть задачи, которые они могут выполнять (1), и другие, которые

они не могут (0).



1 2 3 4 5 6 7 8 9 10
1 1 0 1 1 1 1 0 0 1 1
2 0 1 0 0 0 1 0 0 1 0
3 0 1 0 0 1 1 0 0 1 0
4 0 0 1 0 0 1 0 0 1 0
5 1 0 0 1 1 1 0 0 0 0
6 0 0 1 1 1 0 1 0 1 1
7 1 1 0 0 1 0 1 0 0 0
8 1 0 0 1 1 1 1 0 1 1
9 0 0 1 0 1 0 1 0 1 0
10 0 1 0 1 1 0 1 0 0 0
11 0 1 0 0 1 0 1 0 0 0
12 1 1 0 1 0 1 0 1 0 1
13 1 1 0 1 0 0 1 1 0 0
14 1 1 0 1 0 1 0 1 0 0
15 1 1 0 0 1 0 0 1 0 1
16 0 1 0 1 0 1 0 1 0 0
17 0 0 1 0 0 1 0 1 0 0
18 0 1 0 0 0 0 0 1 0 1
19 1 1 1 1 1 1 1 0 1 0
20 0 0 0 0 0 1 0 0 1 1
21 0 1 0 0 1 0 0 0 1 0
22 1 1 0 1 0 0 1 0 1 1
23 1 0 1 0 0 0 1 0 1 1
24 1 0 0 1 1 0 1 0 1 1
25 1 0 0 0 0 0 1 0 1 1

Каждый оператор имеет:

  • Максимальное время работы.
  • фиксированную стоимость.
1 2 3 4 5 6 7 8 9 10
Costs 35 34 38 41 42 50 39 31 25 29
Maximum Times 100 80 70 70 50 40 80 90 50 50

Ограничения:

  • Для каждой выполненненной задачи, количество невыполненных задач с более высоким приоритетом, чем она не может превышать 2 (чем выше цифра приоритета — тем больше приоритет).
  • У компании есть лимит расходов G=900, который не должен быть превышен.

Цель — максимизировать количество выполненных задач.

Беру задачу «Optprob/Выбор ребер и узлов в графе» себе!


Есть неориентированный граф, список ребер…

Надо выбрать пять узлов и десять ребер (по два соседствующих с каждым ребром на каждый узел), так, чтобы сумма весов всех этих ребер будет минимальна.

Беру задачу «Optprob/Производство и распределение» себе!


Производство и распределение 2023-12-23 04-51-11 image0.png

Компания имеет два завода, на которых производятся единицы ее продукции.

Каждый завод i имеет

  • ежедневную производственную мощность K(i) единиц продукции
  • небольшой склад, емкостью FA(i)
Factories
IdFAK
120,0005,000
225,0003,500

Предположим, что для производства требуется L=5 рабочих дней в неделю.

Еще у компании есть два склада-хаба, откуда произведенная продукция рассылается потребителям. У каждого склада j есть

  • Вместимость Aj
  • Способность ежедневной отгрузки Ej
Hubs
IdAjEj
110,0005,000
250,0004,000


Есть

Между потребителями, фабриками и хабами есть расстояния:

Фабрика-Хаб
Distance_F_H
HubDistanceFactory
11501
24001
135002
21002


хаб-хаб
Distance_H_H
Hub2DistanceHub1
25001
15002

Поставлять продукты потребителям можно и с завода, и любого хаба, можно перемещать продукты между хабами, в любом случае, вне зависимости от расстояния «поставка» происходит на следующий день (будем считать, что основные затраты времени процессные, а не от перевозки).

Производство и распределение 2022-11-17 15-17-39 image0.png

Надо смоделировать производство и перемещение продуктов между заводом-хабами-потребителями, чтобы минимизировать

суммарное за неделю общее расстояние всех перевозок (количество продуктов не важно, условная фура вмещает все эти мелкие продукты).

Беру задачу «Optprob/Плантации» себе!


Плантатор планирует оптимальные посадки сельхоз культур на своих участках.

Он владеет N=20 участками с площадями (м²) 

 800 700 800 1000 5000 10000 4000 25000 40000 10000 5000 10000 4000 25000 40000 5000 10000 4000 25000 40000
Плантации 2023-12-23 04-23-38 image0.png

Участки могут граничить, и это выражается матрицей 

1 0 0 0 0 0 0 0 0 0 0 0 1 1 0 0 0 0 0 1
0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 1 0 1 0 0 1 0 0 1 0 0 1 0 0 0 0 0 0
0 0 0 1 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 1 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0
0 0 0 0 0 1 0 0 0 1 0 1 0 1 0 0 1 0 0 1
0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 1 0 0 0 0 1 0 0 0 1 0 0 0
0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 1 0
0 0 0 0 0 0 0 0 0 1 0 0 0 1 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 1 1 0 0 0
0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 1 0 0
0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 1 0 1 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 1 0 1 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 1 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1

Он может посадить 4 культуры (пшеницу, кукурузу, овес и оливки). Есть

  • минимальный план посадок,
  • есть доход/выручка на каждый квадратный метр для каждой культуры,
  • есть фиксированные затраты на засев культурой любого участка
Культура (i) Необходимо посадить D_i м² Выручка на м² Фиксированные затраты на участок
пшеница 50000 100 40
кукуруза 20000 200 10
овес 30000 150 15
оливки 20000 200 20

И, в зависимости от участка, есть переменные затраты на квадратный метр каждой культуры 

10 12 14 13 14 15 17 13 12 10 10 12 11 9 8 7 9 5 6 7 
7 7 7 7 8 8 9 9 10 5 5 5 5 9 8 7 9 5 6 7 
12 11 9 8 7   9 5 6 7 8  12 14 13 14 15   17 13 12 10 10 
6 12 14 13 14  15 17 13 12 10  10 12 11 9 8  7 9 5 6 7  ~

И ограничения хитрой агрикультурной магии:

  • Каждый участок можно
    • не засевать
    • либо засевать максимум двумя культурами.

Но

  • Пшеницу нельзя совмещать на участке с другими культурами.
  • Нельзя растить на одном и даже соседних участках
    • кукурузу и пшеницу
    • курурузу и овес

Нужно понять, что и где сеять, чтобы максимизировать прибыль.

Беру задачу «Optprob/Онлайн-распродажа в овощном магазине» себе!


Онлайн-распродажа 2023-12-23 03-34-51 image0.png

Овощной магазин продает 45 различных товаров онлайн, включая фрукты, овощи и всякое такое.

25 из них продаются килограммами, KS — запасы этих продуктов на складе:


1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
KS 200 300 500 400 300 500 350 550 350 330 400 400 450 500 500 300 200 200 120 120 200 300 400 500 500

а KV — объем каждого килограмма продукта:



1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
KV 10 25 32 45 40 20 20 20 30 32 33 45 54 10 20 30 10 30 40 10 20 20 30 30 30


Остальные 20 товаров продаются единицами, их запасы на складе US:

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
US 300 250 250 500 450 400 150 240 260 450 340 340 500 500 400 400 300 300 200 300


А объем каждого штучного товара — UV:


1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
UV 10 20 10 15 15 20 30 30 35 45 14 13 12 10 20 20 15 20 20 10


Каждый заказ упаковывается в коробки, разных типов, и надо решить, в какой из них отправлять

  • есть четыре модели коробок, каждая с определенным объемом.
  • имеется достаточный запас коробок любой модели.

1 2 3 4
V 200 300 400 500

Мы получили 100 заказов, в каждом из которых заказано определенное количество килограмм каждой позиции весового товара:

И также, матрица заказов штучных товаров:

Вполне может получится, что не все заказы могут быть выполнены. Но каждый принятый заказ надо выполнить полностью. При этом надо как-то экономно распределить их по коробкам

Целевая функция — минимизация суммы объема отправленных коробок плюс штраф в десятикратном размере за объем оставшихся на складе товаров.

Беру задачу «Optprob/Выбор проекта» себе!


Выбор проекта 2023-12-23 03-02-55 image0.png

Компания рассматривает пять проектов.

Каждый утвержденный проект будет выполняться в 3-летний период.

Ожидаемые доходы и ежегодные расходы по каждому проекту, а также доступные годовые средства в тысячах евро:

Выбор проекта 2022-10-21 16-48-44 image0.png

Компания, принимая во внимание имеющийся у нее капитал, должна выбирать проекты с целью максимизации общей доходности.

Кроме того:

  • Проект 3 не может быть выбран, если он выбран проект 5.
  • Проекты 1 и 2 завершаются совместно только в том случае, если не завершены оба — проект 4, и проект 5.
  • Компания должна сократить свои свободные средства на 5000 долларов в течение одного из 3 лет и должна решить, в каком году это сделать.

Есть решение студента, которое, несмотря на правильные цифры с солвером SCIP, концептуально неверно — формулируется не ЦЛП модель (надо научится именно ставить ЦЛП-модели). Так что можно ознакомится с «почти готовым решением», доработать его, и представить задачу. Разумеется, посмотрите разборы решений от Стаса Фомина, чтобы оформлять не так как здесь, а гибко и эффективно (компактные модели порождаемые функцией, использование хелперов и т.п.)


Беру задачу «Optprob/Парковки для электромобилей» себе!


Парковки для электромобилей 2023-12-23 03-46-32 image0.png

Город разделен на 18 районов.

Городской совет хочет установить в городе парковочные места для электромобилей (PSEC),

и подход, который он хочет сделать, заключается в том, чтобы сбалансировать установку PSEC в зависимости от количества электромобилей, которыми владеет каждый район.

PSEC могут быть установлены двумя способами: по отдельности или парами (два смежных

PSEC устанавливаются с двойным дозатором).

Стоимость отдельного PSEC составляет CI, в то время как общая стоимость двух PSEC на пару составляет CD.

Бюджет, доступный для проекта, составляет P.

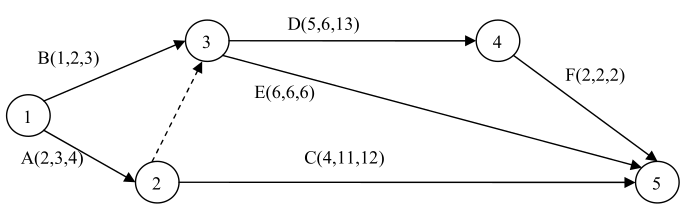
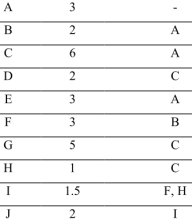
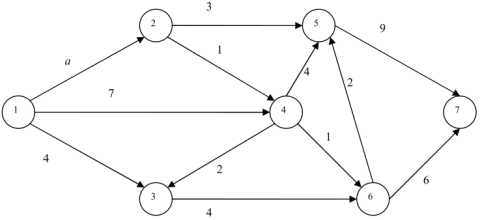
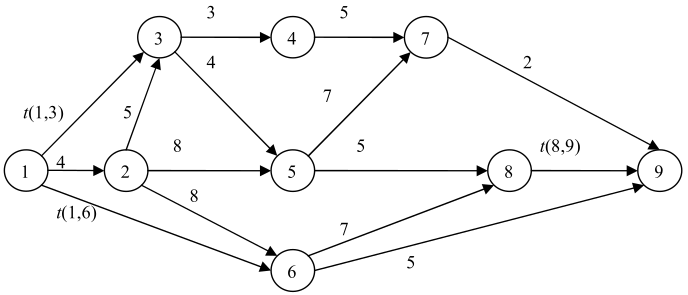
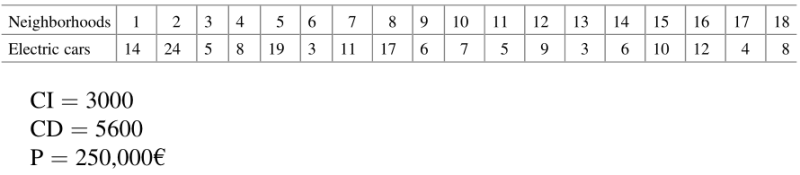
Парковки для электромобилей 2022-10-21 13-28-41 image0.png

[ Хронологический вид ]Комментарии

(нет элементов)

Войдите, чтобы комментировать.

Источник — «https://discopal.ispras.ru/index.php?title=Открытые_бизнес-задачи&oldid=21653»