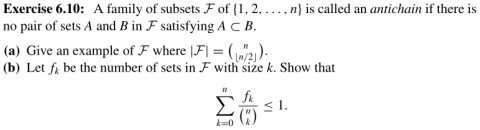Open Exercises — различия между версиями
StasFomin (обсуждение | вклад) (Копия ревизии 25388 статьи Open Classic Hard Problems) |
StasFomin (обсуждение | вклад) |
||
| Строка 7: | Строка 7: | ||
template=IncludeCard2 | template=IncludeCard2 | ||
redirect=no | redirect=no | ||
| − | category= | + | category=Теоретические_задачи |
notcategory=Solved | notcategory=Solved | ||
ignore=Permission denied | ignore=Permission denied | ||
ignore=A | ignore=A | ||
| − | ignore=Open | + | ignore=Open Exercises |
</templatedpagelist> | </templatedpagelist> | ||
Версия 09:38, 19 мая 2023
Всего страниц найдено: 235.
Задача «Задачи/eupce-6-2-a»©
Докажите, что для каждого целого числа n существует раскраска ребер полного графа в два цвета, такое что полное число одноцветных подграфов
Задача «Задачи/eupce-6-4»©
Проверено: StasFomin 13:14, 21 декабря 2024 (UTC)
Рассмотрим игру, основанную на бросках трех стандартных шестисторонних костей. Цель → получить одинаковое число на всех трех костях, кто первый этого добьется, тот выиграл.
- Игрок начинает с броска всех трех кубиков.
- После первого броска игрок может выбрать одну, две или три кости и бросить их снова.
- После второго броска игрок один из трех кубиков и перебросить его.
Предположим, что игрок использует следующую оптимальную стратегию:
- если все три кости одинаковые → останавливаемся и выигрываем;
- если два кубика совпадают, игрок перебрасывает тот, который «выбивается из коллектива».
- если все не совпадают — перебрасываем их всех.
Найдите вероятность того, что ровно два из трех кубиков показывают одинаковое число в первом броске.
Задача «Задачи/dtime-n2-is-closed-carp-reduction»©
- Класс сложности С замкнут относительно какой-то сводимости, если L→L' и
P^{\Sigma^p_{k}}=P^{\Pi^p_{k}} , то . Рассмотрим класс .
Замкнут ли он относительно полиномиальной сводимости по Карпу?
Задача «Задачи/eupce-2-13-b»©
Решите обобщенную версию задачи [[../eupce-2-13]]:
- kn различных купонов, организованных в n непересекающихся наборов из k купонов.
- нужен один купон из каждого набора.
Задача зарезервирована: MordashovAP 14:41, 20 декабря 2024 (UTC)
Задача «Задачи/NTIME-NlogN-reduction-3SAT»©
Покажите, что для любого языка
Задача зарезервирована: Nikitashapovalov 00:04, 20 декабря 2024 (UTC)
Задача «Задачи/DHAM3»©
Пусть
-
[b_1, b_2, \ldots, b_{2^{n-1}}] — задача поиска гамильтонового цикла в графеb_1 = \max \{a_1, a_2\} , где V — делиться на 3. -
b_2 = \max \{a_3, a_4\} — задача подтверждения наличия гамильтонового цикла в таком графе.
Докажите, что
Задача зарезервирована: Nikitashapovalov 00:03, 20 декабря 2024 (UTC)
Задача «Задачи/conp-as-yes»©
Покажите, что язык L лежит в co-NP тогда и только тогда, если существует недетерминированная машина M, и полином p, такой, что M останавливается за время p(n) для всех входов x длины n, и L состоит точно только из таких строк x, у которых все пути вычисления M(x) приводят к ответу «1».
Задача зарезервирована: Nikitashapovalov 23:59, 19 декабря 2024 (UTC)
Задача «Задачи/Свойство Sigma i=PH»©
.
Задача зарезервирована: Nikitashapovalov 23:54, 19 декабря 2024 (UTC)
Задача «Задачи/unary-in-p-then-time2kn-in-time2cn»©
Докажите, что если каждый унарный язык из NP также лежит в P, то
то для любого языка из
Задача зарезервирована: Nikitashapovalov 23:51, 19 декабря 2024 (UTC)
Задача «Задачи/Квадрат букв»©
Задача зарезервирована: илья52 21:51, 19 декабря 2024 (UTC)
Задача «Задачи/eupce-6-9»©
Задача зарезервирована: илья52 21:50, 19 декабря 2024 (UTC)
Задача «Задачи/eupce-6-20»©
Задача зарезервирована: илья52 21:49, 19 декабря 2024 (UTC)
Задача «Задачи/eupce-1-16-d»©
Задача зарезервирована: илья52 21:49, 19 декабря 2024 (UTC)
Рассмотрим игру, основанную на бросках трех стандартных шестисторонних костей. Цель → получить одинаковое число на всех трех костях, кто первый этого добьется, тот выиграл.
- Игрок начинает с броска всех трех кубиков.
- После первого броска игрок может выбрать одну, две или три кости и бросить их снова.
- После второго броска игрок один из трех кубиков и перебросить его.
Предположим, что игрок использует следующую оптимальную стратегию:
- если все три кости одинаковые → останавливаемся и выигрываем;
- если два кубика совпадают, игрок перебрасывает тот, который «выбивается из коллектива».
- если все не совпадают — перебрасываем их всех.
Рассматривая все возможные возможные выпадения костей, найдите вероятность того, что игрок выиграет.
Задача «Задачи/eupce-6-14»©
Задача зарезервирована: илья52 21:25, 19 декабря 2024 (UTC)
Задача «Задачи/eupce-1-16-a»©
Рассмотрим игру, основанную на бросках трех стандартных шестисторонних костей.
Цель → получить одинаковое число на всех трех костях, кто первый этого добьется, тот выиграл.
- Игрок начинает с броска всех трех кубиков.
- После первого броска игрок может выбрать одну, две или три кости и бросить их снова.
- После второго броска игрок один из трех кубиков и перебросить его.
Предположим, что игрок использует следующую оптимальную стратегию:
- если все три кости одинаковые → останавливаемся и выигрываем;
- если два кубика совпадают, игрок перебрасывает тот, который «выбивается из коллектива».
- если все не совпадают — перебрасываем их всех.
Найдите вероятность того, что все три кубика показывают одинаковое число в первом броске.
Задача зарезервирована: MordashovAP 12:37, 19 декабря 2024 (UTC)
Задача «Задачи/eupce-1-26-b»©
Обычные крестики-нолики скучные, при оптимальной стратегии в них выигрывают крестики. Рассмотрим вероятную модификацию этой игры.
- Как обычно, крестики и нолики ходят по очереди и нолик идет первым. Как обычно, выигрывает тот, кто первый добъется «три в ряд», или ничья, если никто.
- Но на каждом ходе позиция и у крестиков и у ноликов выбирается независимо и равномерно среди свободных квадратов.
Найдите вероятность, выигрыша для «крестиков» и для «ноликов».
Задача зарезервирована: MordashovAP 12:33, 19 декабря 2024 (UTC)
Задача «Задачи/P^BPP»©
Какой класс будет
Задача зарезервирована: NikitaAkshaev 11:40, 18 декабря 2024 (UTC)
Задача «Задачи/eupce-6-1-a»©
Рассмотрим K-ESAT, SAT, когда в каждой скобке ровно k литералов.
Предложите Лас-Вегас алгоритм выполняющий минимум
скобок, и проанализируйте матожидание его времени выполнения.
Задача зарезервирована: NikitaAkshaev 11:28, 18 декабря 2024 (UTC)
Задача «Задачи/eupce-6-3-b»©
Проверено: StasFomin 22:52, 17 декабря 2024 (UTC)
- Дан n-вершинный неориентированный граф G=(V, E).
Рассмотрим следующий метод генерации независимого множества.
Для заданной перестановки вершин σ, определим подмножество S(σ) вершин следующим образом: для каждой вершины i, i ∈ S(σ) тогда и только тогда, когда ни один сосед j вершины i не предшествует i в перестановке σ.
Предложите вероятностный алгоритм для поиска σ
для которого можно показать, что ожидаемый размер
где означает степень вершины i.
Докажите, что в G существует независимое множество размера как минимум
Задача «Задачи/eupce-6-3-a»©
Проверено: StasFomin 22:42, 17 декабря 2024 (UTC)
- Дан n-вершинный неориентированный граф G=(V, E).
Рассмотрим следующий метод генерации независимого множества.
Для заданной перестановки вершин σ, определим подмножество S(σ) вершин следующим образом: для каждой вершины i, i ∈ S(σ) тогда и только тогда, когда ни один сосед j вершины i не предшествует i в перестановке σ.
Покажите, что каждый S(σ) будет независимым множеством в G.
Задача зарезервирована: Конин Георгий 10:48, 13 декабря 2024 (UTC)
Задача «Задачи/eupce-6-19»©
Проверено: StasFomin 21:10, 17 декабря 2024 (UTC)
Задача «Задачи/eupce-1-11-b»©
Проверено: StasFomin 08:40, 17 декабря 2024 (UTC)
- Пытаемся передать один бит (0 или 1) через промежуточные узлы, каждый из которых независимо может инвертировать бит с вероятностью «p».
- Скажем, узел имеет смещение «q», если это , «смещение» будет вещественным числом на отрезке [−1, 1].
Докажите, что прохождение бита через узлы со смещениями «q1» и «q2» эквивалентно прохождению бита через один узел со смещением «q1×q2».
Задача «Задачи/eupce-6-10»©
Задача зарезервирована: Trifonov.dv 19:15, 15 декабря 2024 (UTC)
Задача «Задачи/eupce-6-7»©
Задача зарезервирована: Glbmkrv 02:35, 15 декабря 2024 (UTC)
Задача «Задачи/eupce-2-7-a»©
X и Y — независимые случайные величины с геометрическим распределением, с параметрами P и Q соответственно.
P(X = Y) = ?
Задача зарезервирована: Галлямов Ислам М05-304б 15:36, 13 декабря 2024 (UTC)
Задача «Задачи/eupce-1-14»©
Задача зарезервирована: Ydanyok 15:32, 13 декабря 2024 (UTC)
Я играю в турнире ракетбола против игрока, против которого раньше не играл, но видел его в игре.
Априори рассматриваю три равновероятные возможности:
- мы одинаково талантливы, каждый из нас в равной степени может выиграть каждую игру;
- Я немного лучше, и поэтому я выигрываю каждую игру независимо с вероятностью 0.6;
- Он немного лучше, и поэтому он выигрывает каждую игру независимо с вероятностью 0.6.
В рокетбол играют, пока один игрок не выиграет три сета. В нашей игре, я выиграл только второй сет, а противник выиграл первый, третий и четвертый.
В апостеорной модели, с какой вероятностью я должен верить, что мой оппонент немного лучше, чем я?
Задача «Задачи/accept-after-t-steps-in-npc»©
Задача зарезервирована: Ydanyok 09:10, 13 декабря 2024 (UTC)
- M
- одноленточная машина Тьюринга над бинарным алфавитом.
- t
- число t единичной системе (t единиц).
- Существует вход x, M(x) останавливается и возвращает 1, после t шагов.
Покажите, что это NP-полная задача.
Задача «Задачи/Жадное вершинное покрытие для почти всех исходных данных»©
Задача зарезервирована: Ydanyok 09:03, 13 декабря 2024 (UTC)
- n-вершин
- ребра между любой парой вершин возникают с вероятностью p.
Какова точность алгоритма для почти всех исходных данных?
(упрощенный вариант — для фиксированного p=½).
Задача «Задачи/eupce-1-26-a»©
Задача зарезервирована: Ydanyok 09:03, 13 декабря 2024 (UTC)
Обычные крестики-нолики скучные, при оптимальной стратегии в них выигрывают крестики. Рассмотрим вероятную модификацию этой игры.
- Изначально, бросая честную монетку, разметим каждый из девяти квадратов либо X, либо O.
- Если только один из игроков имеет «три в ряд» → он победил.
- Если оба или никто → ничья.
Определите вероятность, что «X» выиграет.
Задача «Задачи/eupce-2-9»©
Задача зарезервирована: Галлямов Ислам М05-304б 13:43, 9 декабря 2024 (UTC)
Дважды бросают честный k-гранный кубик с числами от 1 от k до k на гранях кубика, получая значения X1 и X2.
- E[max(X1, X2)] = ?
- E[min(X1, X2)] = ?
Покажите, что E[max(X1 , X2)] + E[min(X1 , X2)] = E[X1] + E[X2].
Задача «Задачи/eupce-2-6-d»©
Предположим, что независимо бросают два стандартных шестисторонних кости, X1 — то, что выпадает на первой, X2 — на второй, а X — сумма обоих значений.
- 2 ≤ k ≤ 12
- E[X1 - X2 | X = k] = ?
Задача зарезервирована: RomanFilonov 20:42, 8 декабря 2024 (UTC)
Задача «Задачи/eupce-1-11-c»©
Пытаемся передать один бит (0 или 1) через «n» промежуточных узлов, каждый из которых независимо
может инвертировать бит с вероятностью «p».
Докажите, что вероятность получения корректного бита:
Задача зарезервирована: RomanFilonov 19:10, 8 декабря 2024 (UTC)
Задача «Задачи/eupce-1-9»©
- Честную монету бросили «n» раз.
- Для k>0, найдите верхнюю границу вероятности, что будет последовательность из последовательных орлов.
Задача зарезервирована: RomanFilonov 15:46, 8 декабря 2024 (UTC)
Задача «Задачи/eupce-6-8»©
Задача зарезервирована: Конин Георгий 20:59, 3 декабря 2024 (UTC)
Задача «Задачи/eupce-6-11»©
Задача зарезервирована: AlferovIS 20:54, 1 декабря 2024 (UTC)
Задача «Задачи/eupce-2-6-c»©
Предположим, что независимо бросают два стандартных шестисторонних кости, X1 — то, что выпадает на первой, X2 — на второй, а X — сумма обоих значений.
E[X1 | X = 9] = ?
Задача зарезервирована: AlferovIS 16:19, 1 декабря 2024 (UTC)
Задача «Задачи/eupce-2-13»©
- Каждая коробка хлопьев содержит один из 2n различных купонов (купон в каждой коробке выбирается независимо и равномерно случайным образом из 2n).
- Купоны организованы в n пар, так что купоны 1 и 2 составляют пару, купоны 3 и 4 составляют пару и так далее.
- Получив по одному купону из каждой пары, вы можете получить приз.
Какое ожидаемое количество коробок, надо для этого купить?
Задача зарезервирована: AlferovIS 16:11, 1 декабря 2024 (UTC)
Задача «Задачи/eupce-2-5»©
Если X — случайная величина с биномиальным распределением B(n, 1/2) для n ≥ 1, покажите, что вероятность того,
что X — четное будет 1/2.
Задача зарезервирована: AlferovIS 16:09, 1 декабря 2024 (UTC)
Задача «Задачи/eupce-6-17»©
Проверено: StasFomin 09:07, 27 ноября 2024 (UTC)
Задача зарезервирована: LunevLA 19:21, 25 ноября 2024 (UTC)
Задача «Задачи/eupce-2-6-a»©
Проверено: StasFomin 08:59, 27 ноября 2024 (UTC)
Предположим, что независимо бросают два стандартных шестисторонних кости, X1 — то, что выпадает на первой, X2 — на второй, а X — сумма обоих значений.
E[X | X1 — четное] = ?
Задача «Задачи/eupce-2-6-b»©
Предположим, что независимо бросают два стандартных шестисторонних кости, X1 — то, что выпадает на первой, X2 — на второй, а X — сумма обоих значений.
E[X | X1 = X2] = ?
Задача зарезервирована: LunevLA 15:06, 25 ноября 2024 (UTC)
Задача «Задачи/NP-sums»©
Проверить принадлежность классу следующей задачи: по заданному конечному множеству натуральных чисел, представленных в своей бинарной записи, определить возможность разделения этого множества на два подмножества с одинаковыми суммами.
Задача зарезервирована: LunevLA 16:01, 23 ноября 2024 (UTC)
Задача «Задачи/eupce-2-8-a»©
Алиса и Боб решили заводить детей до тех пор, пока у них не родится девочка или пока у них не будет k ≥ 1 детей.
Предположим, что каждый ребенок будет мальчиком или девочкой независимо с вероятностью 1/2 и что многоплодных родов не бывает.
- Каково ожидаемое число детей женского пола?
- Каково ожидаемое число детей мужского пола?
Задача зарезервирована: LunevLA 15:45, 23 ноября 2024 (UTC)
Задача «Задачи/eupce-6-15»©
Задача зарезервирована: EjenY 15:43, 10 ноября 2024 (UTC)
Задача «Задачи/eupce-2-7-c»©
Задача зарезервирована: Solovev 15:16, 10 ноября 2024 (UTC)
X и Y — независимые случайные величины с геометрическим распределением, с параметрами P и Q соответственно.
P(min(X, Y) = k) = ?
Задача «Задачи/eupce-2-4»©
Докажите, что для любого целого
Задача зарезервирована: Ermakov
Задача «Задачи/eupce-1-13»©
Медицинская компания рекламирует свой новый тест на определенное заболевание.
Частота ошибок первого рода (false negative) мала: если у вас есть расстройство, вероятность того, что тест вернет положительный результат, составляет 0.999.
Частота ошибок второго рода (false positive) тоже невелика: если у вас нет расстройства, вероятность того, что тест вернет положительный результат, составляет всего 0.005.
Предположим, что эту болезнь имеет 2% населения.
Если мы проверяем человека, выбранного равномерно из популяции, и получается положительный результат, какова вероятность того, что эта болезнь у него действительно есть?
Задача зарезервирована: Ermakov
Задача «Задачи/eupce-1-15»©
Предположим, что бросают десять стандартных шестисторонних костей.
Какова вероятность того, что их сумма будет деленной на 6, предполагая, что броски независимы?
Задача зарезервирована: Ermakov
Задача «Задачи/MAX-CUT-NPC»©
Докажите, что задача MAX-CUT, в форме задачи разрешения («правда, ли, что для графа G есть разрез больше K?») NP-полна.
Задача зарезервирована: Ermakov
Задача «Задачи/eupce-1-11-a»©
Проверено: StasFomin 12:29, 26 декабря 2023 (UTC)
Пытаемся передать один бит (0 или 1) через «n» промежуточных узлов, каждый из которых независимо может инвертировать бит с вероятностью «p».
Докажите, что вероятность получения корректного бита:
s(a)∈ Z^+
Задача «Задачи/3csat-npc»©
Задача «Задачи/unary-in-p-then-exptime-nexp»©
Докажите, что если каждый унарный язык из NP также лежит в P, то EXPTIME=NEXP.
Задача «Задачи/eupce-2-7-b»©
Проверено: StasFomin 06:51, 18 декабря 2023 (UTC)
E[max(X, Y)] = ?
Задача «Задачи/eupce-2-7-d»©
X и Y — независимые случайные величины с геометрическим распределением, с параметрами P и Q соответственно.
E[X | X ≤ Y] = ?
Задача «Задачи/compliment-in-ph»©
Задача «Задачи/eupce-1-10»©
Проверено: StasFomin 06:41, 18 декабря 2023 (UTC)
Есть нормальная честная монета и фальшивая, с двумя «решками». Допустим, что мы
- выбираем одну из двух монет случайным образом,
- подбрасываем ее
- выпала решка.
Какова вероятность, что мы выбрали фальшивую монету?
Задача «Задачи/eupce-1-12»©
Проверено: StasFomin 12:00, 15 декабря 2023 (UTC)
Есть три коробки. В одной миллион рублей, в двух других — 100р.
Игра играется следующим образом:
- Участник выбирает коробку.
- Ведущий открывает одну из других коробок, чтобы убедить, что там всего — 100р.
- Участник может выбрать первоначально выбранную коробку или переключится на другую (разумеется, логично выбрать не ту, где показали 100 р).
Итак, если участник сменит выбранную на первом шаге коробку, увеличит ли это его шансы?
Задача «Задачи/eupce-2-12»©
Проверено: StasFomin 07:51, 24 мая 2023 (UTC)
Мы берем карты равномерно случайным образом с из колоды из n карт, выбранную карту добавляют в колоду (она будет всегда полна).
- Каково ожидаемое число карт, которые мы должны вытянуть, пока не увидим все n карт в колоде?
- Если мы возьмем 2n карт, то каково ожидаемое число карт в колоде, которые
- не будут выбраны вообще?
- выбраны ровно один раз?
Задача «Задачи/eupce-6-5»©
Проверено: StasFomin 07:50, 24 мая 2023 (UTC)
Покажите, что в графе с n вершинами и m ребрами, существует разрез, размера как минимум mn/(2n-1).
Задача «Задачи/eupce-2-1»©
Проверено: StasFomin 07:49, 24 мая 2023 (UTC)
Задача «Задачи/eupce-2-8-b»©
Проверено: StasFomin 09:48, 21 мая 2023 (UTC)
Предположим, что Алиса и Боб решили продолжать заводить детей, пока у них не родится девочка.
Если предположить, что это возможно, то каково ожидаемое количество мальчиков у них родится?
Задача «Задачи/eupce-1-23»©
Проверено: StasFomin 09:42, 21 мая 2023 (UTC)
В графе может быть несколько одинаково минимальных разрезов. Покажите, что их не больше n(n − 1)/2.
Задача «Задачи/eupce-6-1-b»©
">живьем в лабе
Предложите алгоритм дерандомизации методом условных вероятностей для алгоритма из MAX-SAT: вероятностное округление/Задачи/eupce-6-1-a.
Задача «Задачи/eupce-1-18»©
- Есть функция
\pi: [1..m]→ [1..m] - и известно что
d\left(\{c_{\pi(m)},c_{\pi(1)}\}\right)+\displaystyle\sum\limits_{i=1}^{m-1} d\left(\{c_{\pi(i)},c_{\pi(i+1)}\}\right) .
Единственный способ вычисления F — использовать таблицу поиска, в которой хранится значения F.
К сожалению, злой противник изменил значение 1/5 записей в этой таблице.
Опишите простой рандомизированный алгоритм, который, учитывая входной Z, выводит значение, которое равняется f(z) с вероятностью не менее 1/2.
Ваш алгоритм должен работать для каждого значения Z, независимо от того, какие записи изменил противник.
Дополнительно, предположим, вам разрешено повторить этот ваш начальный алгоритм три раза.
Как этим воспрользоваться, чтобы максимально увеличить вероятность правильного ответа, и какова эта вероятность?
Задача «Задачи/E13SAT-NPC»©
Покажите, что NP-полна и такая вариация 3SAT, когда язык состоит из таких 3КНФ, которые
- выполнимы
- и в этом выполняющем наборе, в каждой скобке ровно один истинный литерал.
Задача «[[Открытые теоретические задачи|]]»©
Всего страниц найдено: 10.
Задача «Задачи/eupce-6-1-b»©
Предложите алгоритм дерандомизации методом условных вероятностей для алгоритма из MAX-SAT: вероятностное округление/Задачи/eupce-6-1-a.
Задача «Задачи/eupce-1-18»©
- Есть функция
- и известно что .
Единственный способ вычисления F — использовать таблицу поиска, в которой хранится значения F. К сожалению, злой противник изменил значение 1/5 записей в этой таблице.
Опишите простой рандомизированный алгоритм, который, учитывая входной Z, выводит значение, которое равняется f(z) с вероятностью не менее 1/2.
Ваш алгоритм должен работать для каждого значения Z, независимо от того, какие записи изменил противник.
Дополнительно, предположим, вам разрешено повторить этот ваш начальный алгоритм три раза.
Как этим воспрользоваться, чтобы максимально увеличить вероятность правильного ответа, и какова эта вероятность?
Задача «Задачи/ptas-for-minimal-scheduling»©
Разработайте PTAS-алгоритм для Планирование Задач на Одинаковых Машинах используя этот подход.
Задача «Задачи/maximum-k-choice-knapsack-dynamic-programming»©
Придумайте алгоритм динамического программирования, находящий оптимальное решение задачи Maximum Integer k-choice Knapsack.
Задача «Задачи/scheduling-ident-machines-in-npc»©
Рассмотрим задачу разрешения для оптимизационной задачи Планирование Задач на Одинаковых Машинах («если ли планировка с максимальным временем меньше k»).
Покажите, что эта задача, даже в случае p=2, NP-полна.
Задача «Задачи/USUBSETSUM-IN-P»©
Вспомним задачу булев-рюкзак выполнимость, и потребуем, чтобы все веса и размер рюкзака задавались в унарной системе ().
Покажите, что тогда язык таких выполнимых рюкзаков, лежит в классе P.
Задача «Задачи/QBEQ-NPC-NPC»©
Покажите NP-полноту языка совместимых систем квадратичных уравнений в булевых переменных. Т.е. разрешимых систем вида
и где сложение по модулю 2.
Задача «Задачи/\Sigma^p k=NP^(\Sigma^p (k-1))»©
Докажите
Задача «Задачи/P^(\Sigma^p k)=P^(\Pi^p k)»©
Докажите
Задача «Задачи/Порядок закачек — NPC»©
Представим распределенный сервис стриминга видеофильмов. Центральный сервер с полной БД фильмов получает от периферийных кеширующих узлов запросы на требуемые фильмы и ориентировочные сроки, когда люди собираются их посмотреть.
Однако пропускная способность от сервера с дисками к внешнему миру ограничена, и требуется составить работающее расписание отгрузки фильмов.
Конкретно, узел контроля планирования получает n-заданий вида:
- «начать_не_раньше, закончить_не_позже, размер_фильма»i, 1<=i<=n
- максимальная пропускная способность не больше МаксКанал
И говорит «OK» (или «Паника-Паника!» в противном случае), если существует такое расписание из n команд отгрузки, соответствующих заданию (1<=i<=n ):
- «время_начала, время_окончания, ширина_канала»i,
- время_началаi >= начать_не_раньшеi
- время окончанияi <= закончить_не_позжеi
- ширина_каналаi <= МаксКанал
- ширина_канала*(время_окончания — время_начала)i >= размер_фильмаi
Докажите NP-полноту задачи.
Hint: Можно через «Рюкзак-выполнимость» или «SUBSET-SUM»
Задача «Задачи/\Sigma^p k=NP^(\Sigma^p (k-1))»©
Докажите
Задача «Задачи/QBEQ-NPC-NPC»©
Покажите NP-полноту языка совместимых систем квадратичных уравнений в булевых переменных. Т.е. разрешимых систем вида
и где сложение по модулю 2.
Задача «Задачи/USUBSETSUM-IN-P»©
Вспомним задачу булев-рюкзак выполнимость, и потребуем, чтобы все веса и размер рюкзака задавались в унарной системе (
Покажите, что тогда язык
Задача «Задачи/scheduling-ident-machines-in-npc»©
Рассмотрим задачу разрешения для оптимизационной задачи Планирование Задач на Одинаковых Машинах («если ли планировка с максимальным временем меньше k»).
Покажите, что эта задача, даже в случае p=2, NP-полна.
Задача «Задачи/Порядок закачек — NPC»©
Представим распределенный сервис стриминга видеофильмов. Центральный сервер с полной БД фильмов получает от периферийных кеширующих узлов запросы на требуемые фильмы и ориентировочные сроки, когда люди собираются их посмотреть.
Однако пропускная способность от сервера с дисками к внешнему миру ограничена, и требуется составить работающее расписание отгрузки фильмов.
Конкретно, узел контроля планирования получает n-заданий вида:
- «начать_не_раньше, закончить_не_позже, размер_фильма»i, 1<=i<=n
- максимальная пропускная способность не больше МаксКанал
И говорит «OK» (или «Паника-Паника!» в противном случае), если существует такое расписание из n команд отгрузки, соответствующих заданию (1<=i<=n ):
- «время_начала, время_окончания, ширина_канала»i,
- время_началаi >= начать_не_раньшеi
- время окончанияi <= закончить_не_позжеi
- ширина_каналаi <= МаксКанал
- ширина_канала*(время_окончания — время_начала)i >= размер_фильмаi
Докажите NP-полноту задачи.
Hint: Можно через «Рюкзак-выполнимость» или «SUBSET-SUM»
Задача «Задачи/ptas-for-minimal-scheduling»©
Разработайте PTAS-алгоритм для Планирование Задач на Одинаковых Машинах используя этот подход.
Задача «Задачи/maximum-k-choice-knapsack-dynamic-programming»©
Придумайте алгоритм динамического программирования, находящий оптимальное решение задачи Maximum Integer k-choice Knapsack.
Задача «Задачи/P^(\Sigma^p k)=P^(\Pi^p k)»©
Докажите
Задача «Задачи/ex-turing-copy-lowerbound»©
Задача «Задачи/ex-turing-max-time-grows»©
Задача «Задачи/ex-union-decideable-decideable»©
Задача «Задачи/ex-unsolvable-exists»©
Докажите, что существуют невычислимые по Тьюрингу функции y=f(x), используя мощностные соображения.
Задача «Задачи/Возведение в степень за логарифмическое время»©
Формально об алгоритмах. Вычислительные модели.Возведение в степень за логарифмическое время
Постройте RAM-программу, которая по входу (a,b), где a,b > 1, вычисляет ab. Время работы программы должно быть О(log b)
Задача «Задачи/Конкатенция P»©
Задача «Задачи/Разрешимость конкатенации»©
Задача «Задачи/Теорема о неподвижной точке»©
Задача «Задачи/сolorization»©
Не используя факта
Задача «Задачи/ex-greedy-sat-is-2-approx»©
Покажите, что алгоритм Greedy algorithm for SAT находит 2-приближенное решение для MAX SAT (т.е. не хуже оптимального больше чем в два раза).
Задача «Задачи/ex-greedy-sat-is-2-approx-weighted»©
Как задача [[../ex-greedy-sat-is-2-approx]], только покажите, что 2-приближенность сохранится, если будет MAX-SAT-Weighted
Задача «Задачи/ex-sat-average-expect-max-nk»©
Докажите, что (определения см. в тексте лекций или книге):
Покажите, что следующая задача является NP-полной: дан набор из не более чем $n$ типов квадратиков $1\times1$, на сторонах которых написаны какие-то буквы; дан список допустимых пар букв и список граничных букв; спрашивается, можно ли корректно сложить из квадратиков набора большой квадрат размера $n\times n$ (так, чтобы на примыкающих сторонах квадратиков были только допустимые пары букв, а на границе квадрата~--- только граничные буквы).
Задача «Задачи/ex-sat-dynp-bad-data»©
Какие входные данные для алгоритма «alg-sat-dynp» заставят его работать экспоненциально долго?
Задача «Задачи/ex-sat-dynp-good-data»©
На каких входных данных алгоритм из этой темы, будет работать ?
Задача «Задачи/Проблемы определения «в среднем»»©
- Вероятностное распределение
- Вероятность появления каждой входной строки.
- вход длины n.
Задача «Задачи/ex-packing-average-bad-and-good-data»©
- Какие входные данные для алгоритма динамического программирования для упаковки
заставят его работать экспоненциально долго?
- А какие — за ?
Задача «Задачи/MTSP NP-полна»©
Покажите, что метрическая задача коммивояжера NP-полна.
Задача «Задачи/nearest-neighbour-not-good-for-tsp»©
Неграмотный программист, недолго погуглив, решил использовать для задачи оптимизационной коммивояжера TSP алгоритм Nearest neighbour
Докажите, что для любой константы c>1 и для любого n>3,
существует экземпляр TSP с n-городами, на котором этот алгоритм будет находить решение, в С раз хуже (т.е. больше).
Задача «Задачи/nearest-neighbour-tsp-infty-bas-cases»©
Начальная ситуация как в Приближенный алгоритм для метрической задачи коммивояжера/Задачи/nearest-neighbour-not-good-for-tsp.
Покажите, что для любой константы C, таких плохих входных данных (для разных n), бесконечное количество.
Подсказка: для любого i>0, сконструируйте входную задачу, где NN-алгоритм будет находить решение, минимум в (i+2)/6 раз большее оптимального.
Задача «Задачи/Плохой пример»©
Придумайте пример, входной метрический граф, на котором алгоритм Кристофидеса дает наихудшую точность, т.е. 3/2.
Задача «Задачи/Четность вершин нечетной степени в MST»©
Задача «Задачи/sorting-convex-hull»©
Задача «[[Уникальность минимального остовного дерева|]]»©
Задача «Задачи/ex-exists-enumeration-of-halts»©
Существует ли алгоритм, который выписывает одну за другой все машины Тьюринга, которые останавливаются, будучи запущенными на пустой ленте?
Задача «Задачи/ex-halt-empty-tape»©
Докажите, что также неразрешима версия задачи HALT — «остановка на пустом слове», т.е. для данной МТ T определить, остановится ли она на пустом слове.
Задача «Задачи/ex-lost»©
Задача «Задачи/ex-no-enumeration-of-cycled»©
Докажите, что не существует алгоритма, который выписывает одну за другой все машины Тьюринга, которые не останавливаются, будучи запущенными на пустой ленте.
Задача «Задачи/ex-obfuscation-undecidable»©
Беру задачу «Формально об алгоритмах. Вычислительные модели/Задачи/ex-obfuscation-undecidable» себе!
Докажите, что неразрешима «Проблема недостижимого кода» - нет алгоритма, который для заданной машины Тьюринга T и ее состояния выясняет: попадет ли машина в это состояние хотя бы для одного входного слова x?
Задача «Задачи/Tautology in coNP»©
Задача «Задачи/Unary-lang-and-NP»©
Рассмотрим языки, в которых строки-слова состоят только из последовательности нулей. Покажите, что если существует один из таких языков , что , то .
Задача «Задачи/Vcover-clique»©
Задача «Задачи/a^b eq c mod d in P»©
Задача «Задачи/double-sat»©
Язык L состоит из формул SAT, для которых есть по крайней мере два выполняющих набора. Покажите, что .
Задача «Задачи/ex-2sat-in-p»©
Покажите, что задача 2SAT лежит в P.
Задача «Задачи/ex-equiv-in-3knf»©
Выразите логическое отношение эквивалентности в виде 3-КНФ формулы.
Задача «Задачи/ex-hamilton-cycle-in-np»©
Покажите, что
- задача распознавания гамильтоновых графов (т.,е. графов, содержащих гамильтонов цикл) принадлежит NP,
- а задача распознавания негамильтоновых графов (т.,е. графов, не содержащих ни одного гамильтонова цикла)
принадлежит coNP.
Задача «Задачи/ex-limited-3sat-npc»©
Рассмотрим ограниченную версию задачи 3SAT, где на КНФ-формулу дополнительно наложено ограничение, что в ней каждая переменная может входить не больше трех раз, причем каждый литерал - не больше двух.
Покажите, что и эта задача NP-полна.
Задача «Задачи/ex-p-in-np-and-conp»©
Покажите, что .
Задача «Задачи/ex-polynomial-diofant-is-in-np»©
Задача «Задачи/ex-triange-in-p»©
Придумайте полиномиальный алгоритм для проверки, есть ли в заданном графе хотя бы один «треугольник».
Задача «Задачи/k-подсемейство множеств - NPC»©
Докажите NP-полноту следующей проблемы. Исходное данное: конечное семейство конечных множеств и натуральное . Существует ли подсемейство, состоящее из попарно непересекающихся множеств?
Задача «Задачи/knights-np-complete»©
Задача «Задачи/nonapprox TSP»©
Покажите, что если то для задачи коммивояжера не существует полиномиального приближенного алгоритма с мультипликативной ошибкой не превышающей величины, зависящей только от числа вершин графа.
Задача «Задачи/np-closed-under-coding»©
K(L) — кодировка.
Докажите, что класс NP замкнут относительно кодировок.
Т.е. покажите, что если , а KOD — какая-то кодировка над алфавитом L, то
Задача «Задачи/p-looks-unclosed-under-coding»©
K(L) — кодировка.
Докажите, что класс P замкнут относительно кодировок тогда и только тогда, если P=NP.
Задача «Задачи/strong-nmt-good-characterization»©
Пусть есть язык L, для которого
- есть некая МТ M, возвращает «0», «1», «?».
- для любого , все пути вычисления M(x) за полиномиальное время приводят к ответам «1» или «?», при том есть хотя бы один путь к «1».
- для любого , все пути вычисления M(x) за полиномиальное время приводят к ответам «0» или «?», при том есть хотя бы один путь к «0».
Покажите, что
Задача «Задачи/Гамильтонов граф»©
Покажите, что если язык ГАМИЛЬТОНОВ ГРАФ ∈ P , то за полиномиальное время можно не только определить, что граф гамильтонов, но и найти в нем какой-нибудь гамильтонов цикл (если он существует).
Задача «Задачи/НМТ для Subset Sum»©
Постройте недетерминированный полиномиальный алгоритм для задачи Subset Sum
Задача «Задачи/Раскраска графа в два цвета»©
Задача «Задачи/Язык планарных графов»©
Задача «Задачи/tsp-greedy-bad»©
Докажите, что жадный алгоритм в задаче коммивояжера, т.е. алгоритм стартующий с некоторой вершины и пытающийся добавлять наиболее дешевые ребра к еще непосещенным вершинам, не гарантирует нахождение оптимального решения.
Задача «Задачи/Поиск решения уравнения за полиномиальное время»©
Задача «Задачи/Корректность алгоритма Люби»©
Почему в алгоритме Люби построенное множество:
- а) является независимым
- б) максимальным по включению
Задача «Задачи/NP!=co-NP»©
Доказать, что NP ≠ coNP, если P ≠ NP
Задача «Задачи/NP^SAT=\Sigma^p 2»©
Докажите
Задача «Задачи/NP \cup co-NP \subseteq P^NP»©
Докажите
Задача «Задачи/PH \subseteq PSPACE»©
Докажите, что
Задача «Задачи/PH collapse if PHC exists»©
Задача «Задачи/P\poly contains unsolvable»©
Показать, что содержит некоторые невычислимые функции.
Задача «Задачи/P^SAT=P^NP»©
Докажите
Задача «Задачи/3ESAT-NPC»©
Покажите, что 3ESAT — NP-полная задача.
Задача «Задачи/3SAT-TAUTOLOGY-reducibility»©
Покажите, что если 3SAT и TAUTOLOGY полиномиально сводятся к друг другу по Карпу, то NP = CoNP.
Задача «Задачи/3КНФ→Клика»©
Постройте полиномиальную сводимость задачи 3SAT к задаче CLIQUE.
Задача «Задачи/3КНФ→Клика (сохраняя число решений)»©
Получите сводимость как в Полиномиальные сводимости и NP-полные задачи. Классы NP, coNP, NPC/Задачи/3КНФ→Клика, но дополнительно требуется, чтобы количество решений сохранялось.
Т.е. если 3КНФ F полиномиально преобразуется в (граф G, число k), то количество выполняющих наборов переменных для F равно количеству клик размера k в графе G).
Задача «Задачи/HALT-and-NP»©
HALT = {(M,x)} — язык пар (М,x), таких, что машина Тьюринга M останавливается на x за конечное число шагов.
Является ли HALT:
- NP-полным
- NP-трудным
- PSPACE-полным
Задача «Задачи/NPC «k бригад обслуживания»»©
Задача «Задачи/Packing=MaxClique»©
Покажите, что задача об упаковке (в заданном семействе подмножеств найти максимальное число попарно непересекающихся подмножеств) полиномиально эквивалентна задаче о нахождении максимальной клики в графе.
Задача «Задачи/ex-max-maxmatching-1-2»©
Найдите приближенный алгоритм с точностью для нахождения паросочетания максимального размера.
Задача «Задачи/ex-min-maxmatching-1-2»©
Задача «Задачи/exersize-greedy-covering-1»©
Постройте пример, где оценка мультипликативной ошибки жадного алгоритма для задачи покрытия множеств достигается по порядку.
Задача «Задачи/fist-fit-for-vector-packing»©
Рассмотрим многомерное обобщение задачи Упаковки в контейнеры, называемое Vector Packing.
Там размеры всех предметов → d-мерный вектор,
контейнеры тоже d-мерный вектора (V,…,V), и цель — упаковать все предметы в минимум контейнеров, так, чтобы упакованные в контейнеро предметы, после векторного суммирования[1], не вылезали за его границы.
Покажите, что приближенный алгоритм, типа First Fit, обобщенный для многомерности,
найдет (d+1)-оптимальное решение.
Задача «Задачи/graph-coloring-smallest-last-not-good»©
Покажите, что для существенно больших n, существует раскрашиваемый в три цвета граф из n вершин, для которого алгоритм Smallest Last будет использовать цветов.
Задача «Задачи/internal-cover»©
Задача «Задачи/k-cover»©
Предложите k-приближенный полиномиальный алгоритм для задачи о покрытии, когда известно, что в исходных данных, каждый элемент покрывается не более, чем k подмножествами.
Задача «Задачи/lpt-rule-for-scheduling»©
Рассмотрим задачу Планирование Задач на Одинаковых Машинах и применим к ней LPT[2]-эвристику:
- отсортировать задачи по убыванию длины
- для каждой задачи:
- применять жадный алгоритм загрузки: бросать задачу на самую малозагруженную машину
Докажите, что в,
- OPT(x) — значение этого оптимального решения.
- — значение, найденное алгоритмом
Задача «Задачи/lpt-rule-for-scheduling-min-lj»©
Рассмотрим задачу Планирование Задач на Одинаковых Машинах и применим к ней LPT[3]-эвристику:
- отсортировать задачи по убыванию длины
- для каждой задачи:
- применять жадный алгоритм загрузки: бросать задачу на самую малозагруженную машину
Докажите, что в случае этот алгоритм находит оптимальное решение. (OPT(x) — значение этого оптимального решения).
Задача «Задачи/lpt-rule-for-scheduling-p-is-2»©
Рассмотрим задачу Планирование Задач на Одинаковых Машинах и применим к ней LPT[4]-эвристику:
- отсортировать задачи по убыванию длины
- для каждой задачи:
- применять жадный алгоритм загрузки: бросать задачу на самую малозагруженную машину
Докажите, что в случае p=2,
- OPT(x) — значение этого оптимального решения.
- — значение, найденное алгоритмом.
См. также Жадный алгоритм в задачах о покрытии/Задачи/lpt-rule-for-scheduling
Задача «Задачи/minimum-hitting-set-k»©
Рассмотрим задачу Minimum Hitting Set.
Пусть k — максимальный размер подмножеств из C.
Постройте k-оптимальный полиномиальный алгоритм.
- Hint
- Minimum Hitting Set является обобщением минимального вершинного покрытия.
Задача «Задачи/minimum-multicover-approx-with-linear-relaxation»©
Рассмотрим задачу Minimum Multicover.
Придумайте приближенный алгоритм, основанный на линейной релаксации задачи линейного программирования, который находит
P-оптимальное решение, где
Задача «Задачи/vertex-cover»©
Для известного 2-приближенного алгоритма для задачи о вершинном покрытии привести пример графа, для которого «этот алгоритм с паросочетаниями» строит покрытие с числом вершин
Задача «Задачи/Greedy-Subset-Sum»©
Рассмотрим алгоритм, который для любого набора камней произвольного веса разбивает их на две кучи по принципу «очередной камень кладем туда, где суммарный вес меньше». Докажите, что этот приближенный алгоритм имеет мультипликативную ошибку не превышающую 2 (целевая функция — минимизировать максимум по весам в обоих кучах).
Задача «Задачи/sorted weight and cost»©
Предположим, что в задаче о рюкзаке порядок сортировки по увеличению веса совпадает с порядком сортировки по уменьшению cтоимости. Сформулируйте эффективный алгоритм для поиска оптимального решения этой разновидности задачи о рюкзаке и обоснуйте его корректность.
Задача «Задачи/Нижняя оценка точности модифицированного жадного»©
Приведите пример данных, на которых модифицированный жадный алгоритм дает (хотя бы в пределе) наихудшую оценку точности.
Задача «Задачи/Тупая жадность - очень плохо»©
Задача «[[Корректность алгоритма Прима|]]»©
Докажите корректность алгоритма Прима построения минимального остовного дерева взвешенного связного неориентированного графа.
Задача «Задачи/ex-dijksta-not-work-on-negative-weight»©
Приведите пример графа с отрицательными весами, но без циклов отрицательной длины, для которого алгоритм Дейкстры даст неправильный ответ.
Задача «Задачи/ex-fast-power»©
Задача «Задачи/ex-network-reliability»©
Задача «Задачи/l-eq-p-then-pspace-eq-exptime»©
Покажите, что если DLOGSPACE = P, то PSPACE = EXPTIME.
Задача «Задачи/st-connectivity-log-diameter»©
Задача «Задачи/Машина Тьюринга. Количество.»©
Задача «Задачи/замки и ключи»©
Задача «Задачи/Dynamic Voltage Scaling»©
DVS (Dynamic Voltage Scaling) — технология позволяет снижать напряжение на процессоре, и добиваться экономии электроэнергии за счет увеличения времени выполнения задачи.
Пусть процессор поддерживает два уровня напряжения — .
Есть набор из n задач, каждая из которых имеет энергоемкость и время выполнения для обоих режимов~--- т.\,е. :
- энергоемкости
- и
- длительности
- и .
Нужно выполнить все задачи на одном процессоре за время не более T, при этом добиться минимального энергопотребления.
Сведите задачу к классическому оптимизационному рюкзаку.
Задача «Задачи/multidimentional-knapsack-dynamic-programming»©
Придумайте алгоритм динамического программирования для Maximum Integer d-dimentional Knapsack.
Задача «Задачи/workaholic»©
Каждый день можно выбирать между
- отдыхом,
- легкой работой
- или тяжелой работой .
Перед днем тяжелой работы требуется день отдыхать, то есть, если работать день , то нужно отдыхать день .
Если день делать легкую работу, то в день можно делать любую работу или отдыхать. В первый день не разрешается делать тяжелую работу.
Цель, разумеется, выполнить максимальный объем работ.
- Простой жадный алгоритм для этой задачи будет сравнивать с .
- Если тяжелая работа выгоднее, тогда отдыхаем день и выполняем тяжелую в , иначе выполняем легкую.
- Затем рассматриваем день.
Покажите, что для любого $k$, можно представить входные данные , на которых жадный алгоритм выдаст в раз худшее решение.
- Разработайте оптимальный полиномиальный алгоритм, чтобы найти максимальный объем работ за дней, когда известны () для каждого дня.
Задача «Задачи/Гвоздики»©
На прямой дощечке вбиты N гвоздиков.
Любые два гвоздика можно соединить ниточкой.
Требуется соединить некоторые пары гвоздиков ниточками так, чтобы к каждому гвоздику была привязана хотя бы одна ниточка, а суммарная длина всех ниточек была минимальна.
Построить полиномиальный от N алгоритм решающий задачу.
Задача «Задачи/Задача о построении дерева»©
Задача «Задачи/Копейка рубль бережет»©
Задача «Задачи/Худший случай для алгоритма Немхаузера Ульмана»©
Придумайте входные наборы для алгоритма Немхаузера-Ульмана, на которых он будет работать экспоненциальное время.
Задача «Задачи/Худший случай для алгоритма с отбором «дорогих» решений»©
Придумайте входные наборы для этого алгоритма, на которых он будет работать экспоненциальное время.
Задача «Задачи/Худший случай для алгоритма с отбором «легких» решений»©
Придумайте входные наборы для этого алгоритма, на которых он будет работать экспоненциальное время.
Задача «Задача о покрытии отрезков точками»©
Задача «Задачи/Hitting-set»©
Предложите детерминированный приближенный алгоритм для Minimum Hitting Set и оцените его точность.
Решение, по возможности, оформите в виде jupyter notebook.
Задача «Задачи/bin packing problem-first-fit-sometimes-better-than-best-fit»©
Рассмотрим Bin Packing Problem и алгоритмы (там же по ссылке) first fit и best fit.
Найдите примеры входных данных, когда first fit лучше best fit.
Задача «Задачи/bin packing problem-maximize»©
Рассмотрим Bin Packing Problem и модификацию этой задачи — пусть у нас можно потратить эти самые m контейнеров объема V, нет задачи упаковать все предметы, но надо постараться максимизировать число упакованных предметов.
И пусть суммарный вес всех n предметов не больше M*V.
Рассмотрим простой последовательный алгоритм для этого, типа first fit.
- Берем предметы в исходном порядке
- Пытаемся упаковать каждый в первый попавшийся контейнер, в который он лезет.
- Если не лезет ни в один из m, контейнеров, выкидываем этот предмет.
Докажите, что этот алгоритм упакует как минимум n/2 предметов.
Задача «Задачи/chromatic-numbers-for-graph-with-degree»©
Задача «Задачи/chromatic-numbers-for-graphs»©
Задача «Задачи/ex-acyclic-subgraph-1-2»©
Решение, по возможности, оформите в виде jupyter notebook.
Задача «Задачи/ex-greedy-covering-bound-asymptotic»©
Постройте пример, где для жадного алгоритма в задаче о покрытии множеств оценка достигается асимптотически.
Задача «Задачи/ex-greedy-k-covering-bound-asymptotic»©
Задача «Задачи/ex-zpp-notnull»©
Задача «Задачи/las-vegas-k-ammplification»©
Пусть A — вероятностный алгоритм, возращающий или правильный ответ f(x), или «?».
- P(A(x)=f(x)) >= p
Алгоритм B — вызывает A, пока не добьется определенного ответа, но не больше k раз.
Оцените k(q) — количество повторений для заданного уровня вероятности правильного ответа q в алгоритме B.
Задача «Задачи/mc-amplification»©
- A — Монте-Карло алгоритм с вероятностью правильного вычисления f(x):
Сколько k(|x|) повторений вызова A надо сделать, чтобы добится вероятности правильного вычисления большей (1-q)?
Если:
Задача «Задачи/random-walk-for-directed-graph»©
Покажите, что метод случайного блуждания не работает для решения задачи связности на ориентированных графах.
Представьте пример ориентированного графа c n вершинами, в котором даже есть путь из s в t, но матожидание нахождения этого или другого пути s→t будет .
Задача «Задачи/Необратимое семейство перестановок»©
Доказать, что существует необратимое семейство перестановок (под перестановками подразумеваются биекции).
Необратимость означает, что для любого вероятностного полиномиального алгоритма для всех достаточно больших вероятность события меньше (случайно взятый длины и случайное бросание алгоритма).
Задача «Задачи/Casino-n-k»©
Игрок приходит в казино с k долларами и играет в игру, где на каждом шаге можно или выиграть 1 доллар, или проиграть 1 доллар с равной вероятностью. Игрок играет до тех пор, пока не проиграет все деньги или пока не выиграет определенную сумму . Какова вероятность, что игрок проиграет все деньги?
Задача «Задачи/Curse-of-dimensionality»©
Задача «Задачи/alice-bob-three-strange-dice»©
После обеда, Алиса и Боб решают, кому платить.
Алиса достала из кармана три честные (все грани выпадают равновероятно), но нестандартные кости с следующими цифрами на гранях:
- A
- 1, 1, 6, 6, 8, 8
- B
- 2, 2, 4, 4, 9, 9
- C
- 3, 3, 5, 5, 7, 7
Правила игры просты:
- Участники берут по одной кости.
- Выбранные кости бросаются
- Проигравший — у кого цифра меньше (одинаковых быть не может), он и платит за обед.
Алиса благородно представляет право выбора первой кости Бобу.
Покажите, что несмотря на это «благородство», что вероятность выигрыша Алисы больше ½.
Задача «Задачи/coin-game-n-k»©
Двое играют в игру, бросая честную монету, — каждый раз выигрывает тот, кому выпал «орел». Игра заканчивается, когда кто-нибудь выиграет n-раз.
Какова вероятность, что проигравший к концу игры выиграет k-раундов?
Задача «Задачи/coin-ten-times»©
Бросаем честную монетку 10 раз. Найдите вероятность следующих событий:
- Одинаковое число «орлов» и «решек».
- Больше «орлов», чем «решек».
- Для всех 0<i<6, i-й и 11-i-й броски будут одинаковы.
- Будет выброшено подряд четыре «орла».
Задача «Задачи/estimate-probability»©
Имеется приближенный алгоритм, который выдает верное значение с вероятностью . Покажите, что можно уменьшить вероятность ошибки с до любой желаемой , выполнив некоторое число экспериментов и взяв среднее значение. Оценить сверху как функцию от .
Задача «Задачи/random-cloning-n-times»©
В аквариуме плавают существа типа A и B. Изначально их двое — A и B. Каждым ходом мы случайно выбираем одно существо, светим на него лучем жизни, после чего оно клонируется (превращается в двух существ такого же типа).
Покажите, что после n-ходов, число существ типа A будет равновероятно распределено между 1 и n+1.
Задача «Задачи/roll-two-dice»©
Бросаем две обычных шестигранных игральных кости. Кости честные, исходы бросков независимы. Найдите вероятнотсь следующих событий:
- Выпадут два одинаковых результата.
- Число на первой кости больше, чем на второй.
- Сумма обоих результатов — четная.
- Произведение результатов — квадрат какого-то целого числа.
Задача «Задачи/PSPACE in EXPTIME»©
Докажите, что .
Задача «Задачи/QSAT in PSPACE»©
QSAT — это обобщение SAT, когда можно использовать кванторы существования и всеобщности к каждой переменной.
Если кванторы у всех переменных, то свободных переменных нет, и можно спрашивать — истинна ли формула или нет?
Пример:
Задача «Задачи/SAT-in-LOGSPACE»©
Задача «Задачи/dlogspace-pspace-gap»©
Покажите, что должно выполняться хотя бы одно из неравенств (несовпадений) классов сложности:
- DLOGSPACE ≠ P
- PSPACE ≠ P
- Заметим, что если у вас вряд ли получится доказать эти неравенства по отдельности.
Задача «Задачи/ex-braces-parse-in-logspace»©
Задача «Задачи/ex-limited-halt»©
Задача «Задачи/ex-logspace-in-p»©
Задача «Задачи/merge-vertices»©
Минимальный разрез в графе (стягивание вершин)
Рассмотрим рандомизированный алгоритм Каргера-Штейна для неориентированных графов с кратными ребрами. Пусть дан мультиграф c вершинами и ребрами.
Алгоритм основан на операции стягивания ребра между двумя вершинами. После стягивания ребра получим новый граф без вершины в котором каждое ребро вида заменено ребром (петли также удаляются).
Алгоритм следующий
for i=0 to n-2: выбрать случайное ребро e стянуть ребро e
В конце, «восстанавливаем разрез» — каждая его часть соответствует вершинам, содержащимся в одной из метавершин.
Доказать, что вероятностный алгоритм вычисляет минимальный разрез с вероятностью
Задача «Задачи/Верхняя оценка разреза в случайном графе»©
Оцените сверху матожидание числа «больших» разрезов (разрезов, больше чем , где с<8), в случайных графах из n вершин с вероятностью зарождения ребра — ½.
- Hint
- Сначала надо правильно решить MAX-CUT: вероятностное округление/Задачи/Матожидание разреза.
Задача «Задачи/Детерминированный 2-приближенный алгоритм для задачи MAX-CUT»©
Предложите детерминированный 2-приближенный полиномиальный алгоритм для задачи MAX-CUT.
Задача «Задачи/Матожидание разреза»©
Рассмотрим случайные графы
- из n вершин,
- ребро возникает между любой парой вершин с вероятностью ½.
Напишите формулу матожидания средней величины разреза по всем таким случайным графам из n-вершин.
Задача «Задачи/MAX-3ESAT»©
Рассмотрим задачу «MAX-3ESAT», это «MAX-SAT», только в КНФ в каждой скобке ровно три литерала.
Предложите вероятностный алгоритм с точностью .
Задача «Задачи/max-sat-local-opt--1-2»©
Опишите алгоритм локального поиска для MAX-SAT, покажите, что он находит решение не хуже половины от оптимума.
Задача «Задачи/не более половины скобок»©
Приведите пример задачи max-sat (невырожденный случай, т.е. КНФ для любого числа переменных, а не просто пустая формула), для которой на любом наборе переменных выполнено не более половины скобок.
- А менее половины скобок?
Задача «Задачи/2-приближенный алгоритм для максимальной совместной подсистемы»©
Задача «Задачи/ex-derand-maxsat-f0-f1»©
Задача «Задачи/shell-game»©
Честный попутчик в поезде предлагает вам сыграть в следующую игру, вариант классического «наперстка». т. е. есть
- три наперстка,
- шарик,
- ваша задача
- обнаружить шарик - тогда вы выигрываете,
- иначе - выигрывает сдающий.
Каждый раз на кон, вы и сдающий, ставите по 50 рублей.
Сдающий тасует три наперстка, и прячет под одним из них шарик.
Затем он предлагает вам выбрать наперсток.
После того, как вы выбрали наперсток (пусть это будет наперсток «A»), вы можете
- открыть его, либо,
- заплатив еще 10 рублей, потребовать от сдающего, открыть пустой наперсток из двух оставшихся (пусть открытый будет «B»), после чего выбрать один из двух закрытых наперстков (т.е. «A» или «С»).
Заметим, что сдающий и предметы честные — никаких «исчезающих» шариков и прочего мошенничества, наперсток для шарика выбирается совершенно случайно.
Какая стратегия оптимальна?
- Не играть. Выигрыш - «0».
- Выбрать наперсток «A» и открыть его.
- Выбрать наперсток «A», «купить» открытие пустого наперстка «B», но выбрать наперсток «A».
- Выбрать наперсток «A», «купить» открытие пустого наперстка «B», и выбрать наперсток «С».
Дорога длинная, играть можно много раз, правильная стратегия может привести к существенному обогащению, неправильная - к разорению…
Обоснуйте.
Подсчитайте матожидание выигрыша для каждой из стратегий.
Задача «Задачи/Комбинированная дерандомизация»©
А можно ли добиться путем дерандомизации построения -приближенного детерминированного полиномиального алгоритма для задачи MAX-SAT?
Задача «Задачи/TSP-approx»©
Покажите, что если существует полиномиальный f(n)-приближенный алгоритм для задачи о коммивояжере на полном графе с положительными весами, где f любая функция, то P=NP.
Задача «Задачи/ex-max2sat-in-npc»©
Рассмотрим максимизационную версию задачи 2SAT, где дополнительно к 2SAT-формуле задается параметр K, и спрашивается, можно ли выполнить больше чем K, количество скобок.
Покажите, что эта задача NP-полна.
Задача «Задачи/Перечислимость описаний»©
Является ли
- а). перечислимым
- б). ко-перечислимым множество описаний машин Тюринга, останавливающихся на пустом входе?
Ответ обосновать.
Задача «Задачи/Порядок»©
Пусть -- перечислимый язык. Доказать, что если его слова можно лексикографически упорядочить, то тогда является и разрешимым.
Задача «Задачи/determinant»©
Задача «Задачи/BPP in PSPACE»©
Докажите, что .
Не используя теорему Лаутемана (не палите из пушек по воробьям!).
Просто посмотрите на определения обоих классов.
Задача «Задачи/RP in PPoly»©
Докажите, что .
Задача «Задачи/amplify-optimization»©
Есть оптимизационный алгоритм A, который для входа x находит оптимальное решение с вероятностью 1/|x|.
Как сделать из него максимально эффективный алгоритм B, чтобы
Prob(B(x)=OPT) → 1 при |x|→∞.
Задача «Задачи/amplify-when-specific-error-bounded»©
Пусть A — вероятностный алгоритм, вычисляющий f(x).
Но не очень полезный:
- Prob(A(x)=f(x)) >= ⅓
Правда известен факт, что для любого неверного результата w
- Prob(A(x)=w) <= ¼
Можно ли как-то из A сделать полезный алгоритм?
Задача «Задачи/ex-fix-spoj-23»©
Задача «Задачи/ex-fix-spoj-recovery»©
Все то же, что и в упражнении Вероятностные вычисления. Классы RP, coRP, ZPP, BPP/Задачи/ex-fix-spoj-23.
Задача «Задачи/0.5-приближенный вероятностный для MAX-CUT»©
Задача «Задачи/2-boolean system»©
Задача «Задачи/ex-maxcut-trivial-greedy-1-2»©
Студент предлагает для невзвешенной задачи MAX-CUT приближенный алгоритм с точностью ½:
- положить первую вершину в одну часть, последнюю — в другую,
- затем по-очереди добавлять оставшиеся вершины, к множеству, с которым у этой вершины меньше ребер-связей.
Прав ли студент?
Задача «Задачи/ex-min-maxmatching-1-2»©
Задача «Задачи/max-cut-equal-partition-polinomial-local-search»©
Рассмотрим частную версию задачи MAX-CUT — потребуем, чтобы граф был с четным числом вершин, а делить вершины надо на две одинаковые команды.
Придумайте полиномиальный алгоритм для этой задачи.
Задача «[[Зарезервированные практические задачи|]]»©
Всего страниц найдено: 163.
----
Задача «Документолаб»
Задача зарезервирована: берется Шептяков Артём
- https://gitlab.ispras.ru/discopal/docs-research-x
- Также вводно-актуальное: [1], [2]
- Windows-проект! Для тех, у кого винда!
Задача «Understand RTOS»
Задача зарезервирована: Иван Солодовников занялся Embox
- Можно тут параллельно что-то делать с NuttX
Задача «2019-gate-computer-science-and-it-practice.pdf/Q23-alg5»
Вопрос: Q23-alg5-31d68c
Вопрос из «Algorithms Test 5» где-то со страницы 243.
Тут вставьте перевод вопроса.
Используйте возможности разметки, включая формулы и т.п, если будут графы — посмотрите как задать их текстом https://wiki.4intra.net/Graphviz (реально оценю, полезный навык). Если код — теги «code-pascal», «code-c» или «code-python» (не «source lang»).
В IT вообще не принято писать романы, всегда старайтесь писать структурированные (списками-абзацами тексты). Списки в MediaWiki — это просто «*». Не забывайте о них.
Преформатированный моноширинный текст — просто отступ.
Старайтесь нетривиальные понятия, особенно незнакомые вам, найти ссылку на википедию и вставить (нейросети лажают!).
Это важно, чтобы найти корректный перевод (то, что в википедии, или на худой конец — точно массово гуглится).
Потом конечно сотрите эти инструкции, которые тут курсивом или в блоке цитирования.
Ответы
Если ответы простые, однострочные, используйте простой способ задания ответов списком, типа так (префикс «Правильный ответ:» — это дословно, для правильного ответа, неважно, какой он будет в списке)
- Правильный ответ: тут реально правильный ответ
- неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
Если ответы длинные, многострочные, или там графы, используйте способ задания ответов разделами, Но такое очень редко встречается, например 2011-gre-cs-practice-book.pdf/Q05.
Объяснение
Сначала заполните номер страницы с этим вопросом Исходники — вопрос 23 на тут-номер-страницы-с-вопросом-23 странице книги «2019-gate-computer-science-and-it-practice.pdf»
Если все сделаете правильно, по ссылке выше будет открываться правильная страница в правильном PDFе.
Ну и наконец, вики-разметкой напишите ваше понимание, почему правильный ответ — правильный, а неправильные варианты — неправильны.
Тут тоже могут быть полезны ссылки на википедию, решение вами рекуррентных уравнений в sympy.
Задача зарезервирована: StasFomin 15:10, 25 декабря 2024 (UTC)
Задача «2019-gate-computer-science-and-it-practice.pdf/Q24-alg5»
Вопрос: Q24-alg5-31d68c
Вопрос из «Algorithms Test 5» где-то со страницы 243.
Тут вставьте перевод вопроса.
Используйте возможности разметки, включая формулы и т.п, если будут графы — посмотрите как задать их текстом https://wiki.4intra.net/Graphviz (реально оценю, полезный навык). Если код — теги «code-pascal», «code-c» или «code-python» (не «source lang»).
В IT вообще не принято писать романы, всегда старайтесь писать структурированные (списками-абзацами тексты). Списки в MediaWiki — это просто «*». Не забывайте о них.
Преформатированный моноширинный текст — просто отступ.
Старайтесь нетривиальные понятия, особенно незнакомые вам, найти ссылку на википедию и вставить (нейросети лажают!).
Это важно, чтобы найти корректный перевод (то, что в википедии, или на худой конец — точно массово гуглится).
Потом конечно сотрите эти инструкции, которые тут курсивом или в блоке цитирования.
Ответы
Если ответы простые, однострочные, используйте простой способ задания ответов списком, типа так (префикс «Правильный ответ:» — это дословно, для правильного ответа, неважно, какой он будет в списке)
- Правильный ответ: тут реально правильный ответ
- неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
Если ответы длинные, многострочные, или там графы, используйте способ задания ответов разделами, Но такое очень редко встречается, например 2011-gre-cs-practice-book.pdf/Q05.
Объяснение
Сначала заполните номер страницы с этим вопросом Исходники — вопрос 24 на тут-номер-страницы-с-вопросом-24 странице книги «2019-gate-computer-science-and-it-practice.pdf»
Если все сделаете правильно, по ссылке выше будет открываться правильная страница в правильном PDFе.
Ну и наконец, вики-разметкой напишите ваше понимание, почему правильный ответ — правильный, а неправильные варианты — неправильны.
Тут тоже могут быть полезны ссылки на википедию, решение вами рекуррентных уравнений в sympy.
Задача зарезервирована: StasFomin 15:10, 25 декабря 2024 (UTC)
Задача «2019-gate-computer-science-and-it-practice.pdf/Q25-alg5»
Вопрос: Q25-alg5-31d68c
Вопрос из «Algorithms Test 5» где-то со страницы 243.
Тут вставьте перевод вопроса.
Используйте возможности разметки, включая формулы и т.п, если будут графы — посмотрите как задать их текстом https://wiki.4intra.net/Graphviz (реально оценю, полезный навык). Если код — теги «code-pascal», «code-c» или «code-python» (не «source lang»).
В IT вообще не принято писать романы, всегда старайтесь писать структурированные (списками-абзацами тексты). Списки в MediaWiki — это просто «*». Не забывайте о них.
Преформатированный моноширинный текст — просто отступ.
Старайтесь нетривиальные понятия, особенно незнакомые вам, найти ссылку на википедию и вставить (нейросети лажают!).
Это важно, чтобы найти корректный перевод (то, что в википедии, или на худой конец — точно массово гуглится).
Потом конечно сотрите эти инструкции, которые тут курсивом или в блоке цитирования.
Ответы
Если ответы простые, однострочные, используйте простой способ задания ответов списком, типа так (префикс «Правильный ответ:» — это дословно, для правильного ответа, неважно, какой он будет в списке)
- Правильный ответ: тут реально правильный ответ
- неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
Если ответы длинные, многострочные, или там графы, используйте способ задания ответов разделами, Но такое очень редко встречается, например 2011-gre-cs-practice-book.pdf/Q05.
Объяснение
Сначала заполните номер страницы с этим вопросом Исходники — вопрос 25 на тут-номер-страницы-с-вопросом-25 странице книги «2019-gate-computer-science-and-it-practice.pdf»
Если все сделаете правильно, по ссылке выше будет открываться правильная страница в правильном PDFе.
Ну и наконец, вики-разметкой напишите ваше понимание, почему правильный ответ — правильный, а неправильные варианты — неправильны.
Тут тоже могут быть полезны ссылки на википедию, решение вами рекуррентных уравнений в sympy.
Задача зарезервирована: StasFomin 15:10, 25 декабря 2024 (UTC)
Задача «2019-gate-computer-science-and-it-practice.pdf/Q21-alg5»
Вопрос: Q21-alg5-31d68c
Вопрос из «Algorithms Test 5» где-то со страницы 243.
Тут вставьте перевод вопроса.
Используйте возможности разметки, включая формулы и т.п, если будут графы — посмотрите как задать их текстом https://wiki.4intra.net/Graphviz (реально оценю, полезный навык). Если код — теги «code-pascal», «code-c» или «code-python» (не «source lang»).
В IT вообще не принято писать романы, всегда старайтесь писать структурированные (списками-абзацами тексты). Списки в MediaWiki — это просто «*». Не забывайте о них.
Преформатированный моноширинный текст — просто отступ.
Старайтесь нетривиальные понятия, особенно незнакомые вам, найти ссылку на википедию и вставить (нейросети лажают!).
Это важно, чтобы найти корректный перевод (то, что в википедии, или на худой конец — точно массово гуглится).
Потом конечно сотрите эти инструкции, которые тут курсивом или в блоке цитирования.
Ответы
Если ответы простые, однострочные, используйте простой способ задания ответов списком, типа так (префикс «Правильный ответ:» — это дословно, для правильного ответа, неважно, какой он будет в списке)
- Правильный ответ: тут реально правильный ответ
- неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
Если ответы длинные, многострочные, или там графы, используйте способ задания ответов разделами, Но такое очень редко встречается, например 2011-gre-cs-practice-book.pdf/Q05.
Объяснение
Сначала заполните номер страницы с этим вопросом Исходники — вопрос 21 на тут-номер-страницы-с-вопросом-21 странице книги «2019-gate-computer-science-and-it-practice.pdf»
Если все сделаете правильно, по ссылке выше будет открываться правильная страница в правильном PDFе.
Ну и наконец, вики-разметкой напишите ваше понимание, почему правильный ответ — правильный, а неправильные варианты — неправильны.
Тут тоже могут быть полезны ссылки на википедию, решение вами рекуррентных уравнений в sympy.
Задача зарезервирована: StasFomin 15:10, 25 декабря 2024 (UTC)
Задача «2019-gate-computer-science-and-it-practice.pdf/Q22-alg5»
Вопрос: Q22-alg5-31d68c
Вопрос из «Algorithms Test 5» где-то со страницы 243.
Тут вставьте перевод вопроса.
Используйте возможности разметки, включая формулы и т.п, если будут графы — посмотрите как задать их текстом https://wiki.4intra.net/Graphviz (реально оценю, полезный навык). Если код — теги «code-pascal», «code-c» или «code-python» (не «source lang»).
В IT вообще не принято писать романы, всегда старайтесь писать структурированные (списками-абзацами тексты). Списки в MediaWiki — это просто «*». Не забывайте о них.
Преформатированный моноширинный текст — просто отступ.
Старайтесь нетривиальные понятия, особенно незнакомые вам, найти ссылку на википедию и вставить (нейросети лажают!).
Это важно, чтобы найти корректный перевод (то, что в википедии, или на худой конец — точно массово гуглится).
Потом конечно сотрите эти инструкции, которые тут курсивом или в блоке цитирования.
Ответы
Если ответы простые, однострочные, используйте простой способ задания ответов списком, типа так (префикс «Правильный ответ:» — это дословно, для правильного ответа, неважно, какой он будет в списке)
- Правильный ответ: тут реально правильный ответ
- неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
Если ответы длинные, многострочные, или там графы, используйте способ задания ответов разделами, Но такое очень редко встречается, например 2011-gre-cs-practice-book.pdf/Q05.
Объяснение
Сначала заполните номер страницы с этим вопросом Исходники — вопрос 22 на тут-номер-страницы-с-вопросом-22 странице книги «2019-gate-computer-science-and-it-practice.pdf»
Если все сделаете правильно, по ссылке выше будет открываться правильная страница в правильном PDFе.
Ну и наконец, вики-разметкой напишите ваше понимание, почему правильный ответ — правильный, а неправильные варианты — неправильны.
Тут тоже могут быть полезны ссылки на википедию, решение вами рекуррентных уравнений в sympy.
Задача зарезервирована: StasFomin 15:10, 25 декабря 2024 (UTC)
Задача «2019-gate-computer-science-and-it-practice.pdf/Q19-alg5»
Вопрос: Q19-alg5-31d68c
Вопрос из «Algorithms Test 5» где-то со страницы 243.
Тут вставьте перевод вопроса.
Используйте возможности разметки, включая формулы и т.п, если будут графы — посмотрите как задать их текстом https://wiki.4intra.net/Graphviz (реально оценю, полезный навык). Если код — теги «code-pascal», «code-c» или «code-python» (не «source lang»).
В IT вообще не принято писать романы, всегда старайтесь писать структурированные (списками-абзацами тексты). Списки в MediaWiki — это просто «*». Не забывайте о них.
Преформатированный моноширинный текст — просто отступ.
Старайтесь нетривиальные понятия, особенно незнакомые вам, найти ссылку на википедию и вставить (нейросети лажают!).
Это важно, чтобы найти корректный перевод (то, что в википедии, или на худой конец — точно массово гуглится).
Потом конечно сотрите эти инструкции, которые тут курсивом или в блоке цитирования.
Ответы
Если ответы простые, однострочные, используйте простой способ задания ответов списком, типа так (префикс «Правильный ответ:» — это дословно, для правильного ответа, неважно, какой он будет в списке)
- Правильный ответ: тут реально правильный ответ
- неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
Если ответы длинные, многострочные, или там графы, используйте способ задания ответов разделами, Но такое очень редко встречается, например 2011-gre-cs-practice-book.pdf/Q05.
Объяснение
Сначала заполните номер страницы с этим вопросом Исходники — вопрос 19 на тут-номер-страницы-с-вопросом-19 странице книги «2019-gate-computer-science-and-it-practice.pdf»
Если все сделаете правильно, по ссылке выше будет открываться правильная страница в правильном PDFе.
Ну и наконец, вики-разметкой напишите ваше понимание, почему правильный ответ — правильный, а неправильные варианты — неправильны.
Тут тоже могут быть полезны ссылки на википедию, решение вами рекуррентных уравнений в sympy.
Задача зарезервирована: StasFomin 15:10, 25 декабря 2024 (UTC)
Задача «2019-gate-computer-science-and-it-practice.pdf/Q16-alg5»
Вопрос: Q16-alg5-31d68c
Вопрос из «Algorithms Test 5» где-то со страницы 243.
Тут вставьте перевод вопроса.
Используйте возможности разметки, включая формулы и т.п, если будут графы — посмотрите как задать их текстом https://wiki.4intra.net/Graphviz (реально оценю, полезный навык). Если код — теги «code-pascal», «code-c» или «code-python» (не «source lang»).
В IT вообще не принято писать романы, всегда старайтесь писать структурированные (списками-абзацами тексты). Списки в MediaWiki — это просто «*». Не забывайте о них.
Преформатированный моноширинный текст — просто отступ.
Старайтесь нетривиальные понятия, особенно незнакомые вам, найти ссылку на википедию и вставить (нейросети лажают!).
Это важно, чтобы найти корректный перевод (то, что в википедии, или на худой конец — точно массово гуглится).
Потом конечно сотрите эти инструкции, которые тут курсивом или в блоке цитирования.
Ответы
Если ответы простые, однострочные, используйте простой способ задания ответов списком, типа так (префикс «Правильный ответ:» — это дословно, для правильного ответа, неважно, какой он будет в списке)
- Правильный ответ: тут реально правильный ответ
- неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
Если ответы длинные, многострочные, или там графы, используйте способ задания ответов разделами, Но такое очень редко встречается, например 2011-gre-cs-practice-book.pdf/Q05.
Объяснение
Сначала заполните номер страницы с этим вопросом Исходники — вопрос 16 на тут-номер-страницы-с-вопросом-16 странице книги «2019-gate-computer-science-and-it-practice.pdf»
Если все сделаете правильно, по ссылке выше будет открываться правильная страница в правильном PDFе.
Ну и наконец, вики-разметкой напишите ваше понимание, почему правильный ответ — правильный, а неправильные варианты — неправильны.
Тут тоже могут быть полезны ссылки на википедию, решение вами рекуррентных уравнений в sympy.
Задача зарезервирована: StasFomin 15:10, 25 декабря 2024 (UTC)
Задача «2019-gate-computer-science-and-it-practice.pdf/Q15-alg5»
Вопрос: Q15-alg5-31d68c
Вопрос из «Algorithms Test 5» где-то со страницы 243.
Тут вставьте перевод вопроса.
Используйте возможности разметки, включая формулы и т.п, если будут графы — посмотрите как задать их текстом https://wiki.4intra.net/Graphviz (реально оценю, полезный навык). Если код — теги «code-pascal», «code-c» или «code-python» (не «source lang»).
В IT вообще не принято писать романы, всегда старайтесь писать структурированные (списками-абзацами тексты). Списки в MediaWiki — это просто «*». Не забывайте о них.
Преформатированный моноширинный текст — просто отступ.
Старайтесь нетривиальные понятия, особенно незнакомые вам, найти ссылку на википедию и вставить (нейросети лажают!).
Это важно, чтобы найти корректный перевод (то, что в википедии, или на худой конец — точно массово гуглится).
Потом конечно сотрите эти инструкции, которые тут курсивом или в блоке цитирования.
Ответы
Если ответы простые, однострочные, используйте простой способ задания ответов списком, типа так (префикс «Правильный ответ:» — это дословно, для правильного ответа, неважно, какой он будет в списке)
- Правильный ответ: тут реально правильный ответ
- неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
Если ответы длинные, многострочные, или там графы, используйте способ задания ответов разделами, Но такое очень редко встречается, например 2011-gre-cs-practice-book.pdf/Q05.
Объяснение
Сначала заполните номер страницы с этим вопросом Исходники — вопрос 15 на тут-номер-страницы-с-вопросом-15 странице книги «2019-gate-computer-science-and-it-practice.pdf»
Если все сделаете правильно, по ссылке выше будет открываться правильная страница в правильном PDFе.
Ну и наконец, вики-разметкой напишите ваше понимание, почему правильный ответ — правильный, а неправильные варианты — неправильны.
Тут тоже могут быть полезны ссылки на википедию, решение вами рекуррентных уравнений в sympy.
Задача зарезервирована: StasFomin 15:10, 25 декабря 2024 (UTC)
Задача «2019-gate-computer-science-and-it-practice.pdf/Q11-alg5»
Вопрос: Q11-alg5-31d68c
Вопрос из «Algorithms Test 5» где-то со страницы 243.
Тут вставьте перевод вопроса.
Используйте возможности разметки, включая формулы и т.п, если будут графы — посмотрите как задать их текстом https://wiki.4intra.net/Graphviz (реально оценю, полезный навык). Если код — теги «code-pascal», «code-c» или «code-python» (не «source lang»).
В IT вообще не принято писать романы, всегда старайтесь писать структурированные (списками-абзацами тексты). Списки в MediaWiki — это просто «*». Не забывайте о них.
Преформатированный моноширинный текст — просто отступ.
Старайтесь нетривиальные понятия, особенно незнакомые вам, найти ссылку на википедию и вставить (нейросети лажают!).
Это важно, чтобы найти корректный перевод (то, что в википедии, или на худой конец — точно массово гуглится).
Потом конечно сотрите эти инструкции, которые тут курсивом или в блоке цитирования.
Ответы
Если ответы простые, однострочные, используйте простой способ задания ответов списком, типа так (префикс «Правильный ответ:» — это дословно, для правильного ответа, неважно, какой он будет в списке)
- Правильный ответ: тут реально правильный ответ
- неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
Если ответы длинные, многострочные, или там графы, используйте способ задания ответов разделами, Но такое очень редко встречается, например 2011-gre-cs-practice-book.pdf/Q05.
Объяснение
Сначала заполните номер страницы с этим вопросом Исходники — вопрос 11 на тут-номер-страницы-с-вопросом-11 странице книги «2019-gate-computer-science-and-it-practice.pdf»
Если все сделаете правильно, по ссылке выше будет открываться правильная страница в правильном PDFе.
Ну и наконец, вики-разметкой напишите ваше понимание, почему правильный ответ — правильный, а неправильные варианты — неправильны.
Тут тоже могут быть полезны ссылки на википедию, решение вами рекуррентных уравнений в sympy.
Задача зарезервирована: StasFomin 15:10, 25 декабря 2024 (UTC)
Задача «2019-gate-computer-science-and-it-practice.pdf/Q12-alg5»
Вопрос: Q12-alg5-31d68c
Вопрос из «Algorithms Test 5» где-то со страницы 243.
Тут вставьте перевод вопроса.
Используйте возможности разметки, включая формулы и т.п, если будут графы — посмотрите как задать их текстом https://wiki.4intra.net/Graphviz (реально оценю, полезный навык). Если код — теги «code-pascal», «code-c» или «code-python» (не «source lang»).
В IT вообще не принято писать романы, всегда старайтесь писать структурированные (списками-абзацами тексты). Списки в MediaWiki — это просто «*». Не забывайте о них.
Преформатированный моноширинный текст — просто отступ.
Старайтесь нетривиальные понятия, особенно незнакомые вам, найти ссылку на википедию и вставить (нейросети лажают!).
Это важно, чтобы найти корректный перевод (то, что в википедии, или на худой конец — точно массово гуглится).
Потом конечно сотрите эти инструкции, которые тут курсивом или в блоке цитирования.
Ответы
Если ответы простые, однострочные, используйте простой способ задания ответов списком, типа так (префикс «Правильный ответ:» — это дословно, для правильного ответа, неважно, какой он будет в списке)
- Правильный ответ: тут реально правильный ответ
- неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
Если ответы длинные, многострочные, или там графы, используйте способ задания ответов разделами, Но такое очень редко встречается, например 2011-gre-cs-practice-book.pdf/Q05.
Объяснение
Сначала заполните номер страницы с этим вопросом Исходники — вопрос 12 на тут-номер-страницы-с-вопросом-12 странице книги «2019-gate-computer-science-and-it-practice.pdf»
Если все сделаете правильно, по ссылке выше будет открываться правильная страница в правильном PDFе.
Ну и наконец, вики-разметкой напишите ваше понимание, почему правильный ответ — правильный, а неправильные варианты — неправильны.
Тут тоже могут быть полезны ссылки на википедию, решение вами рекуррентных уравнений в sympy.
Задача зарезервирована: StasFomin 15:10, 25 декабря 2024 (UTC)
Задача «2019-gate-computer-science-and-it-practice.pdf/Q09-alg5»
Вопрос: Q09-alg5-31d68c
Вопрос из «Algorithms Test 5» где-то со страницы 243.
Тут вставьте перевод вопроса.
Используйте возможности разметки, включая формулы и т.п, если будут графы — посмотрите как задать их текстом https://wiki.4intra.net/Graphviz (реально оценю, полезный навык). Если код — теги «code-pascal», «code-c» или «code-python» (не «source lang»).
В IT вообще не принято писать романы, всегда старайтесь писать структурированные (списками-абзацами тексты). Списки в MediaWiki — это просто «*». Не забывайте о них.
Преформатированный моноширинный текст — просто отступ.
Старайтесь нетривиальные понятия, особенно незнакомые вам, найти ссылку на википедию и вставить (нейросети лажают!).
Это важно, чтобы найти корректный перевод (то, что в википедии, или на худой конец — точно массово гуглится).
Потом конечно сотрите эти инструкции, которые тут курсивом или в блоке цитирования.
Ответы
Если ответы простые, однострочные, используйте простой способ задания ответов списком, типа так (префикс «Правильный ответ:» — это дословно, для правильного ответа, неважно, какой он будет в списке)
- Правильный ответ: тут реально правильный ответ
- неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
Если ответы длинные, многострочные, или там графы, используйте способ задания ответов разделами, Но такое очень редко встречается, например 2011-gre-cs-practice-book.pdf/Q05.
Объяснение
Сначала заполните номер страницы с этим вопросом Исходники — вопрос 9 на тут-номер-страницы-с-вопросом-9 странице книги «2019-gate-computer-science-and-it-practice.pdf»
Если все сделаете правильно, по ссылке выше будет открываться правильная страница в правильном PDFе.
Ну и наконец, вики-разметкой напишите ваше понимание, почему правильный ответ — правильный, а неправильные варианты — неправильны.
Тут тоже могут быть полезны ссылки на википедию, решение вами рекуррентных уравнений в sympy.
Задача зарезервирована: StasFomin 15:10, 25 декабря 2024 (UTC)
Задача «2019-gate-computer-science-and-it-practice.pdf/Q10-alg5»
Вопрос: Q10-alg5-31d68c
Вопрос из «Algorithms Test 5» где-то со страницы 243.
Тут вставьте перевод вопроса.
Используйте возможности разметки, включая формулы и т.п, если будут графы — посмотрите как задать их текстом https://wiki.4intra.net/Graphviz (реально оценю, полезный навык). Если код — теги «code-pascal», «code-c» или «code-python» (не «source lang»).
В IT вообще не принято писать романы, всегда старайтесь писать структурированные (списками-абзацами тексты). Списки в MediaWiki — это просто «*». Не забывайте о них.
Преформатированный моноширинный текст — просто отступ.
Старайтесь нетривиальные понятия, особенно незнакомые вам, найти ссылку на википедию и вставить (нейросети лажают!).
Это важно, чтобы найти корректный перевод (то, что в википедии, или на худой конец — точно массово гуглится).
Потом конечно сотрите эти инструкции, которые тут курсивом или в блоке цитирования.
Ответы
Если ответы простые, однострочные, используйте простой способ задания ответов списком, типа так (префикс «Правильный ответ:» — это дословно, для правильного ответа, неважно, какой он будет в списке)
- Правильный ответ: тут реально правильный ответ
- неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
Если ответы длинные, многострочные, или там графы, используйте способ задания ответов разделами, Но такое очень редко встречается, например 2011-gre-cs-practice-book.pdf/Q05.
Объяснение
Сначала заполните номер страницы с этим вопросом Исходники — вопрос 10 на тут-номер-страницы-с-вопросом-10 странице книги «2019-gate-computer-science-and-it-practice.pdf»
Если все сделаете правильно, по ссылке выше будет открываться правильная страница в правильном PDFе.
Ну и наконец, вики-разметкой напишите ваше понимание, почему правильный ответ — правильный, а неправильные варианты — неправильны.
Тут тоже могут быть полезны ссылки на википедию, решение вами рекуррентных уравнений в sympy.
Задача зарезервирована: StasFomin 15:10, 25 декабря 2024 (UTC)
Задача «2019-gate-computer-science-and-it-practice.pdf/Q05-alg5»
Вопрос: Q05-alg5-31d68c
Вопрос из «Algorithms Test 5» где-то со страницы 243.
Тут вставьте перевод вопроса.
Используйте возможности разметки, включая формулы и т.п, если будут графы — посмотрите как задать их текстом https://wiki.4intra.net/Graphviz (реально оценю, полезный навык). Если код — теги «code-pascal», «code-c» или «code-python» (не «source lang»).
В IT вообще не принято писать романы, всегда старайтесь писать структурированные (списками-абзацами тексты). Списки в MediaWiki — это просто «*». Не забывайте о них.
Преформатированный моноширинный текст — просто отступ.
Старайтесь нетривиальные понятия, особенно незнакомые вам, найти ссылку на википедию и вставить (нейросети лажают!).
Это важно, чтобы найти корректный перевод (то, что в википедии, или на худой конец — точно массово гуглится).
Потом конечно сотрите эти инструкции, которые тут курсивом или в блоке цитирования.
Ответы
Если ответы простые, однострочные, используйте простой способ задания ответов списком, типа так (префикс «Правильный ответ:» — это дословно, для правильного ответа, неважно, какой он будет в списке)
- Правильный ответ: тут реально правильный ответ
- неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
Если ответы длинные, многострочные, или там графы, используйте способ задания ответов разделами, Но такое очень редко встречается, например 2011-gre-cs-practice-book.pdf/Q05.
Объяснение
Сначала заполните номер страницы с этим вопросом Исходники — вопрос 5 на тут-номер-страницы-с-вопросом-5 странице книги «2019-gate-computer-science-and-it-practice.pdf»
Если все сделаете правильно, по ссылке выше будет открываться правильная страница в правильном PDFе.
Ну и наконец, вики-разметкой напишите ваше понимание, почему правильный ответ — правильный, а неправильные варианты — неправильны.
Тут тоже могут быть полезны ссылки на википедию, решение вами рекуррентных уравнений в sympy.
Задача зарезервирована: StasFomin 15:10, 25 декабря 2024 (UTC)
Задача «2019-gate-computer-science-and-it-practice.pdf/Q07-alg5»
Вопрос: Q07-alg5-31d68c
Вопрос из «Algorithms Test 5» где-то со страницы 243.
Тут вставьте перевод вопроса.
Используйте возможности разметки, включая формулы и т.п, если будут графы — посмотрите как задать их текстом https://wiki.4intra.net/Graphviz (реально оценю, полезный навык). Если код — теги «code-pascal», «code-c» или «code-python» (не «source lang»).
В IT вообще не принято писать романы, всегда старайтесь писать структурированные (списками-абзацами тексты). Списки в MediaWiki — это просто «*». Не забывайте о них.
Преформатированный моноширинный текст — просто отступ.
Старайтесь нетривиальные понятия, особенно незнакомые вам, найти ссылку на википедию и вставить (нейросети лажают!).
Это важно, чтобы найти корректный перевод (то, что в википедии, или на худой конец — точно массово гуглится).
Потом конечно сотрите эти инструкции, которые тут курсивом или в блоке цитирования.
Ответы
Если ответы простые, однострочные, используйте простой способ задания ответов списком, типа так (префикс «Правильный ответ:» — это дословно, для правильного ответа, неважно, какой он будет в списке)
- Правильный ответ: тут реально правильный ответ
- неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
Если ответы длинные, многострочные, или там графы, используйте способ задания ответов разделами, Но такое очень редко встречается, например 2011-gre-cs-practice-book.pdf/Q05.
Объяснение
Сначала заполните номер страницы с этим вопросом Исходники — вопрос 7 на тут-номер-страницы-с-вопросом-7 странице книги «2019-gate-computer-science-and-it-practice.pdf»
Если все сделаете правильно, по ссылке выше будет открываться правильная страница в правильном PDFе.
Ну и наконец, вики-разметкой напишите ваше понимание, почему правильный ответ — правильный, а неправильные варианты — неправильны.
Тут тоже могут быть полезны ссылки на википедию, решение вами рекуррентных уравнений в sympy.
Задача зарезервирована: StasFomin 15:10, 25 декабря 2024 (UTC)
Задача «2019-gate-computer-science-and-it-practice.pdf/Q08-alg5»
Вопрос: Q08-alg5-31d68c
Вопрос из «Algorithms Test 5» где-то со страницы 243.
Тут вставьте перевод вопроса.
Используйте возможности разметки, включая формулы и т.п, если будут графы — посмотрите как задать их текстом https://wiki.4intra.net/Graphviz (реально оценю, полезный навык). Если код — теги «code-pascal», «code-c» или «code-python» (не «source lang»).
В IT вообще не принято писать романы, всегда старайтесь писать структурированные (списками-абзацами тексты). Списки в MediaWiki — это просто «*». Не забывайте о них.
Преформатированный моноширинный текст — просто отступ.
Старайтесь нетривиальные понятия, особенно незнакомые вам, найти ссылку на википедию и вставить (нейросети лажают!).
Это важно, чтобы найти корректный перевод (то, что в википедии, или на худой конец — точно массово гуглится).
Потом конечно сотрите эти инструкции, которые тут курсивом или в блоке цитирования.
Ответы
Если ответы простые, однострочные, используйте простой способ задания ответов списком, типа так (префикс «Правильный ответ:» — это дословно, для правильного ответа, неважно, какой он будет в списке)
- Правильный ответ: тут реально правильный ответ
- неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
Если ответы длинные, многострочные, или там графы, используйте способ задания ответов разделами, Но такое очень редко встречается, например 2011-gre-cs-practice-book.pdf/Q05.
Объяснение
Сначала заполните номер страницы с этим вопросом Исходники — вопрос 8 на тут-номер-страницы-с-вопросом-8 странице книги «2019-gate-computer-science-and-it-practice.pdf»
Если все сделаете правильно, по ссылке выше будет открываться правильная страница в правильном PDFе.
Ну и наконец, вики-разметкой напишите ваше понимание, почему правильный ответ — правильный, а неправильные варианты — неправильны.
Тут тоже могут быть полезны ссылки на википедию, решение вами рекуррентных уравнений в sympy.
Задача зарезервирована: StasFomin 15:10, 25 декабря 2024 (UTC)
Задача «2019-gate-computer-science-and-it-practice.pdf/Q01-alg5»
Вопрос: Q01-alg5-31d68c
Вопрос из «Algorithms Test 5» где-то со страницы 243.
Тут вставьте перевод вопроса.
Используйте возможности разметки, включая формулы и т.п, если будут графы — посмотрите как задать их текстом https://wiki.4intra.net/Graphviz (реально оценю, полезный навык). Если код — теги «code-pascal», «code-c» или «code-python» (не «source lang»).
В IT вообще не принято писать романы, всегда старайтесь писать структурированные (списками-абзацами тексты). Списки в MediaWiki — это просто «*». Не забывайте о них.
Преформатированный моноширинный текст — просто отступ.
Старайтесь нетривиальные понятия, особенно незнакомые вам, найти ссылку на википедию и вставить (нейросети лажают!).
Это важно, чтобы найти корректный перевод (то, что в википедии, или на худой конец — точно массово гуглится).
Потом конечно сотрите эти инструкции, которые тут курсивом или в блоке цитирования.
Ответы
Если ответы простые, однострочные, используйте простой способ задания ответов списком, типа так (префикс «Правильный ответ:» — это дословно, для правильного ответа, неважно, какой он будет в списке)
- Правильный ответ: тут реально правильный ответ
- неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
Если ответы длинные, многострочные, или там графы, используйте способ задания ответов разделами, Но такое очень редко встречается, например 2011-gre-cs-practice-book.pdf/Q05.
Объяснение
Сначала заполните номер страницы с этим вопросом Исходники — вопрос 1 на тут-номер-страницы-с-вопросом-1 странице книги «2019-gate-computer-science-and-it-practice.pdf»
Если все сделаете правильно, по ссылке выше будет открываться правильная страница в правильном PDFе.
Ну и наконец, вики-разметкой напишите ваше понимание, почему правильный ответ — правильный, а неправильные варианты — неправильны.
Тут тоже могут быть полезны ссылки на википедию, решение вами рекуррентных уравнений в sympy.
Задача зарезервирована: StasFomin 15:10, 25 декабря 2024 (UTC)
Задача «2019-gate-computer-science-and-it-practice.pdf/Q03-alg5»
Вопрос: Q03-alg5-31d68c
Вопрос из «Algorithms Test 5» где-то со страницы 243.
Тут вставьте перевод вопроса.
Используйте возможности разметки, включая формулы и т.п, если будут графы — посмотрите как задать их текстом https://wiki.4intra.net/Graphviz (реально оценю, полезный навык). Если код — теги «code-pascal», «code-c» или «code-python» (не «source lang»).
В IT вообще не принято писать романы, всегда старайтесь писать структурированные (списками-абзацами тексты). Списки в MediaWiki — это просто «*». Не забывайте о них.
Преформатированный моноширинный текст — просто отступ.
Старайтесь нетривиальные понятия, особенно незнакомые вам, найти ссылку на википедию и вставить (нейросети лажают!).
Это важно, чтобы найти корректный перевод (то, что в википедии, или на худой конец — точно массово гуглится).
Потом конечно сотрите эти инструкции, которые тут курсивом или в блоке цитирования.
Ответы
Если ответы простые, однострочные, используйте простой способ задания ответов списком, типа так (префикс «Правильный ответ:» — это дословно, для правильного ответа, неважно, какой он будет в списке)
- Правильный ответ: тут реально правильный ответ
- неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
Если ответы длинные, многострочные, или там графы, используйте способ задания ответов разделами, Но такое очень редко встречается, например 2011-gre-cs-practice-book.pdf/Q05.
Объяснение
Сначала заполните номер страницы с этим вопросом Исходники — вопрос 3 на тут-номер-страницы-с-вопросом-3 странице книги «2019-gate-computer-science-and-it-practice.pdf»
Если все сделаете правильно, по ссылке выше будет открываться правильная страница в правильном PDFе.
Ну и наконец, вики-разметкой напишите ваше понимание, почему правильный ответ — правильный, а неправильные варианты — неправильны.
Тут тоже могут быть полезны ссылки на википедию, решение вами рекуррентных уравнений в sympy.
Задача зарезервирована: StasFomin 15:10, 25 декабря 2024 (UTC)
Задача «2019-gate-computer-science-and-it-practice.pdf/Q22-alg4»
Вопрос: Q22-alg4-31d68c
Вопрос из «Algorithms Test 4» где-то со страницы 238.
Тут вставьте перевод вопроса.
Используйте возможности разметки, включая формулы и т.п, если будут графы — посмотрите как задать их текстом https://wiki.4intra.net/Graphviz (реально оценю, полезный навык). Если код — теги «code-pascal», «code-c» или «code-python» (не «source lang»).
В IT вообще не принято писать романы, всегда старайтесь писать структурированные (списками-абзацами тексты). Списки в MediaWiki — это просто «*». Не забывайте о них.
Преформатированный моноширинный текст — просто отступ.
Старайтесь нетривиальные понятия, особенно незнакомые вам, найти ссылку на википедию и вставить (нейросети лажают!).
Это важно, чтобы найти корректный перевод (то, что в википедии, или на худой конец — точно массово гуглится).
Потом конечно сотрите эти инструкции, которые тут курсивом или в блоке цитирования.
Ответы
Если ответы простые, однострочные, используйте простой способ задания ответов списком, типа так (префикс «Правильный ответ:» — это дословно, для правильного ответа, неважно, какой он будет в списке)
- Правильный ответ: тут реально правильный ответ
- неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
Если ответы длинные, многострочные, или там графы, используйте способ задания ответов разделами, Но такое очень редко встречается, например 2011-gre-cs-practice-book.pdf/Q05.
Объяснение
Сначала заполните номер страницы с этим вопросом Исходники — вопрос 22 на тут-номер-страницы-с-вопросом-22 странице книги «2019-gate-computer-science-and-it-practice.pdf»
Если все сделаете правильно, по ссылке выше будет открываться правильная страница в правильном PDFе.
Ну и наконец, вики-разметкой напишите ваше понимание, почему правильный ответ — правильный, а неправильные варианты — неправильны.
Тут тоже могут быть полезны ссылки на википедию, решение вами рекуррентных уравнений в sympy.
Задача зарезервирована: StasFomin 10:34, 25 декабря 2024 (UTC)
Задача «2019-gate-computer-science-and-it-practice.pdf/Q23-alg4»
Вопрос: Q23-alg4-31d68c
Вопрос из «Algorithms Test 4» где-то со страницы 238.
Тут вставьте перевод вопроса.
Используйте возможности разметки, включая формулы и т.п, если будут графы — посмотрите как задать их текстом https://wiki.4intra.net/Graphviz (реально оценю, полезный навык). Если код — теги «code-pascal», «code-c» или «code-python» (не «source lang»).
В IT вообще не принято писать романы, всегда старайтесь писать структурированные (списками-абзацами тексты). Списки в MediaWiki — это просто «*». Не забывайте о них.
Преформатированный моноширинный текст — просто отступ.
Старайтесь нетривиальные понятия, особенно незнакомые вам, найти ссылку на википедию и вставить (нейросети лажают!).
Это важно, чтобы найти корректный перевод (то, что в википедии, или на худой конец — точно массово гуглится).
Потом конечно сотрите эти инструкции, которые тут курсивом или в блоке цитирования.
Ответы
Если ответы простые, однострочные, используйте простой способ задания ответов списком, типа так (префикс «Правильный ответ:» — это дословно, для правильного ответа, неважно, какой он будет в списке)
- Правильный ответ: тут реально правильный ответ
- неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
Если ответы длинные, многострочные, или там графы, используйте способ задания ответов разделами, Но такое очень редко встречается, например 2011-gre-cs-practice-book.pdf/Q05.
Объяснение
Сначала заполните номер страницы с этим вопросом Исходники — вопрос 23 на тут-номер-страницы-с-вопросом-23 странице книги «2019-gate-computer-science-and-it-practice.pdf»
Если все сделаете правильно, по ссылке выше будет открываться правильная страница в правильном PDFе.
Ну и наконец, вики-разметкой напишите ваше понимание, почему правильный ответ — правильный, а неправильные варианты — неправильны.
Тут тоже могут быть полезны ссылки на википедию, решение вами рекуррентных уравнений в sympy.
Задача зарезервирована: StasFomin 10:34, 25 декабря 2024 (UTC)
Задача «2019-gate-computer-science-and-it-practice.pdf/Q24-alg4»
Вопрос: Q24-alg4-31d68c
Вопрос из «Algorithms Test 4» где-то со страницы 238.
Тут вставьте перевод вопроса.
Используйте возможности разметки, включая формулы и т.п, если будут графы — посмотрите как задать их текстом https://wiki.4intra.net/Graphviz (реально оценю, полезный навык). Если код — теги «code-pascal», «code-c» или «code-python» (не «source lang»).
В IT вообще не принято писать романы, всегда старайтесь писать структурированные (списками-абзацами тексты). Списки в MediaWiki — это просто «*». Не забывайте о них.
Преформатированный моноширинный текст — просто отступ.
Старайтесь нетривиальные понятия, особенно незнакомые вам, найти ссылку на википедию и вставить (нейросети лажают!).
Это важно, чтобы найти корректный перевод (то, что в википедии, или на худой конец — точно массово гуглится).
Потом конечно сотрите эти инструкции, которые тут курсивом или в блоке цитирования.
Ответы
Если ответы простые, однострочные, используйте простой способ задания ответов списком, типа так (префикс «Правильный ответ:» — это дословно, для правильного ответа, неважно, какой он будет в списке)
- Правильный ответ: тут реально правильный ответ
- неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
Если ответы длинные, многострочные, или там графы, используйте способ задания ответов разделами, Но такое очень редко встречается, например 2011-gre-cs-practice-book.pdf/Q05.
Объяснение
Сначала заполните номер страницы с этим вопросом Исходники — вопрос 24 на тут-номер-страницы-с-вопросом-24 странице книги «2019-gate-computer-science-and-it-practice.pdf»
Если все сделаете правильно, по ссылке выше будет открываться правильная страница в правильном PDFе.
Ну и наконец, вики-разметкой напишите ваше понимание, почему правильный ответ — правильный, а неправильные варианты — неправильны.
Тут тоже могут быть полезны ссылки на википедию, решение вами рекуррентных уравнений в sympy.
Задача зарезервирована: StasFomin 10:34, 25 декабря 2024 (UTC)
Задача «2019-gate-computer-science-and-it-practice.pdf/Q25-alg4»
Вопрос: Q25-alg4-31d68c
Вопрос из «Algorithms Test 4» где-то со страницы 238.
Тут вставьте перевод вопроса.
Используйте возможности разметки, включая формулы и т.п, если будут графы — посмотрите как задать их текстом https://wiki.4intra.net/Graphviz (реально оценю, полезный навык). Если код — теги «code-pascal», «code-c» или «code-python» (не «source lang»).
В IT вообще не принято писать романы, всегда старайтесь писать структурированные (списками-абзацами тексты). Списки в MediaWiki — это просто «*». Не забывайте о них.
Преформатированный моноширинный текст — просто отступ.
Старайтесь нетривиальные понятия, особенно незнакомые вам, найти ссылку на википедию и вставить (нейросети лажают!).
Это важно, чтобы найти корректный перевод (то, что в википедии, или на худой конец — точно массово гуглится).
Потом конечно сотрите эти инструкции, которые тут курсивом или в блоке цитирования.
Ответы
Если ответы простые, однострочные, используйте простой способ задания ответов списком, типа так (префикс «Правильный ответ:» — это дословно, для правильного ответа, неважно, какой он будет в списке)
- Правильный ответ: тут реально правильный ответ
- неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
Если ответы длинные, многострочные, или там графы, используйте способ задания ответов разделами, Но такое очень редко встречается, например 2011-gre-cs-practice-book.pdf/Q05.
Объяснение
Сначала заполните номер страницы с этим вопросом Исходники — вопрос 25 на тут-номер-страницы-с-вопросом-25 странице книги «2019-gate-computer-science-and-it-practice.pdf»
Если все сделаете правильно, по ссылке выше будет открываться правильная страница в правильном PDFе.
Ну и наконец, вики-разметкой напишите ваше понимание, почему правильный ответ — правильный, а неправильные варианты — неправильны.
Тут тоже могут быть полезны ссылки на википедию, решение вами рекуррентных уравнений в sympy.
Задача зарезервирована: StasFomin 10:34, 25 декабря 2024 (UTC)
Задача «2019-gate-computer-science-and-it-practice.pdf/Q15-alg4»
Вопрос: Q15-alg4-31d68c
Вопрос из «Algorithms Test 4» где-то со страницы 238.
Тут вставьте перевод вопроса.
Используйте возможности разметки, включая формулы и т.п, если будут графы — посмотрите как задать их текстом https://wiki.4intra.net/Graphviz (реально оценю, полезный навык). Если код — теги «code-pascal», «code-c» или «code-python» (не «source lang»).
В IT вообще не принято писать романы, всегда старайтесь писать структурированные (списками-абзацами тексты). Списки в MediaWiki — это просто «*». Не забывайте о них.
Преформатированный моноширинный текст — просто отступ.
Старайтесь нетривиальные понятия, особенно незнакомые вам, найти ссылку на википедию и вставить (нейросети лажают!).
Это важно, чтобы найти корректный перевод (то, что в википедии, или на худой конец — точно массово гуглится).
Потом конечно сотрите эти инструкции, которые тут курсивом или в блоке цитирования.
Ответы
Если ответы простые, однострочные, используйте простой способ задания ответов списком, типа так (префикс «Правильный ответ:» — это дословно, для правильного ответа, неважно, какой он будет в списке)
- Правильный ответ: тут реально правильный ответ
- неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
Если ответы длинные, многострочные, или там графы, используйте способ задания ответов разделами, Но такое очень редко встречается, например 2011-gre-cs-practice-book.pdf/Q05.
Объяснение
Сначала заполните номер страницы с этим вопросом Исходники — вопрос 15 на тут-номер-страницы-с-вопросом-15 странице книги «2019-gate-computer-science-and-it-practice.pdf»
Если все сделаете правильно, по ссылке выше будет открываться правильная страница в правильном PDFе.
Ну и наконец, вики-разметкой напишите ваше понимание, почему правильный ответ — правильный, а неправильные варианты — неправильны.
Тут тоже могут быть полезны ссылки на википедию, решение вами рекуррентных уравнений в sympy.
Задача зарезервирована: StasFomin 10:34, 25 декабря 2024 (UTC)
Задача «2019-gate-computer-science-and-it-practice.pdf/Q18-alg4»
Вопрос: Q18-alg4-31d68c
Вопрос из «Algorithms Test 4» где-то со страницы 238.
Тут вставьте перевод вопроса.
Используйте возможности разметки, включая формулы и т.п, если будут графы — посмотрите как задать их текстом https://wiki.4intra.net/Graphviz (реально оценю, полезный навык). Если код — теги «code-pascal», «code-c» или «code-python» (не «source lang»).
В IT вообще не принято писать романы, всегда старайтесь писать структурированные (списками-абзацами тексты). Списки в MediaWiki — это просто «*». Не забывайте о них.
Преформатированный моноширинный текст — просто отступ.
Старайтесь нетривиальные понятия, особенно незнакомые вам, найти ссылку на википедию и вставить (нейросети лажают!).
Это важно, чтобы найти корректный перевод (то, что в википедии, или на худой конец — точно массово гуглится).
Потом конечно сотрите эти инструкции, которые тут курсивом или в блоке цитирования.
Ответы
Если ответы простые, однострочные, используйте простой способ задания ответов списком, типа так (префикс «Правильный ответ:» — это дословно, для правильного ответа, неважно, какой он будет в списке)
- Правильный ответ: тут реально правильный ответ
- неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
Если ответы длинные, многострочные, или там графы, используйте способ задания ответов разделами, Но такое очень редко встречается, например 2011-gre-cs-practice-book.pdf/Q05.
Объяснение
Сначала заполните номер страницы с этим вопросом Исходники — вопрос 18 на тут-номер-страницы-с-вопросом-18 странице книги «2019-gate-computer-science-and-it-practice.pdf»
Если все сделаете правильно, по ссылке выше будет открываться правильная страница в правильном PDFе.
Ну и наконец, вики-разметкой напишите ваше понимание, почему правильный ответ — правильный, а неправильные варианты — неправильны.
Тут тоже могут быть полезны ссылки на википедию, решение вами рекуррентных уравнений в sympy.
Задача зарезервирована: StasFomin 10:34, 25 декабря 2024 (UTC)
Задача «2019-gate-computer-science-and-it-practice.pdf/Q19-alg4»
Вопрос: Q19-alg4-31d68c
Вопрос из «Algorithms Test 4» где-то со страницы 238.
Тут вставьте перевод вопроса.
Используйте возможности разметки, включая формулы и т.п, если будут графы — посмотрите как задать их текстом https://wiki.4intra.net/Graphviz (реально оценю, полезный навык). Если код — теги «code-pascal», «code-c» или «code-python» (не «source lang»).
В IT вообще не принято писать романы, всегда старайтесь писать структурированные (списками-абзацами тексты). Списки в MediaWiki — это просто «*». Не забывайте о них.
Преформатированный моноширинный текст — просто отступ.
Старайтесь нетривиальные понятия, особенно незнакомые вам, найти ссылку на википедию и вставить (нейросети лажают!).
Это важно, чтобы найти корректный перевод (то, что в википедии, или на худой конец — точно массово гуглится).
Потом конечно сотрите эти инструкции, которые тут курсивом или в блоке цитирования.
Ответы
Если ответы простые, однострочные, используйте простой способ задания ответов списком, типа так (префикс «Правильный ответ:» — это дословно, для правильного ответа, неважно, какой он будет в списке)
- Правильный ответ: тут реально правильный ответ
- неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
Если ответы длинные, многострочные, или там графы, используйте способ задания ответов разделами, Но такое очень редко встречается, например 2011-gre-cs-practice-book.pdf/Q05.
Объяснение
Сначала заполните номер страницы с этим вопросом Исходники — вопрос 19 на тут-номер-страницы-с-вопросом-19 странице книги «2019-gate-computer-science-and-it-practice.pdf»
Если все сделаете правильно, по ссылке выше будет открываться правильная страница в правильном PDFе.
Ну и наконец, вики-разметкой напишите ваше понимание, почему правильный ответ — правильный, а неправильные варианты — неправильны.
Тут тоже могут быть полезны ссылки на википедию, решение вами рекуррентных уравнений в sympy.
Задача зарезервирована: StasFomin 10:34, 25 декабря 2024 (UTC)
Задача «2019-gate-computer-science-and-it-practice.pdf/Q11-alg4»
Вопрос: Q11-alg4-31d68c
Вопрос из «Algorithms Test 4» где-то со страницы 238.
Тут вставьте перевод вопроса.
Используйте возможности разметки, включая формулы и т.п, если будут графы — посмотрите как задать их текстом https://wiki.4intra.net/Graphviz (реально оценю, полезный навык). Если код — теги «code-pascal», «code-c» или «code-python» (не «source lang»).
В IT вообще не принято писать романы, всегда старайтесь писать структурированные (списками-абзацами тексты). Списки в MediaWiki — это просто «*». Не забывайте о них.
Преформатированный моноширинный текст — просто отступ.
Старайтесь нетривиальные понятия, особенно незнакомые вам, найти ссылку на википедию и вставить (нейросети лажают!).
Это важно, чтобы найти корректный перевод (то, что в википедии, или на худой конец — точно массово гуглится).
Потом конечно сотрите эти инструкции, которые тут курсивом или в блоке цитирования.
Ответы
Если ответы простые, однострочные, используйте простой способ задания ответов списком, типа так (префикс «Правильный ответ:» — это дословно, для правильного ответа, неважно, какой он будет в списке)
- Правильный ответ: тут реально правильный ответ
- неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
Если ответы длинные, многострочные, или там графы, используйте способ задания ответов разделами, Но такое очень редко встречается, например 2011-gre-cs-practice-book.pdf/Q05.
Объяснение
Сначала заполните номер страницы с этим вопросом Исходники — вопрос 11 на тут-номер-страницы-с-вопросом-11 странице книги «2019-gate-computer-science-and-it-practice.pdf»
Если все сделаете правильно, по ссылке выше будет открываться правильная страница в правильном PDFе.
Ну и наконец, вики-разметкой напишите ваше понимание, почему правильный ответ — правильный, а неправильные варианты — неправильны.
Тут тоже могут быть полезны ссылки на википедию, решение вами рекуррентных уравнений в sympy.
Задача зарезервирована: StasFomin 10:34, 25 декабря 2024 (UTC)
Задача «2019-gate-computer-science-and-it-practice.pdf/Q12-alg4»
Вопрос: Q12-alg4-31d68c
Вопрос из «Algorithms Test 4» где-то со страницы 238.
Тут вставьте перевод вопроса.
Используйте возможности разметки, включая формулы и т.п, если будут графы — посмотрите как задать их текстом https://wiki.4intra.net/Graphviz (реально оценю, полезный навык). Если код — теги «code-pascal», «code-c» или «code-python» (не «source lang»).
В IT вообще не принято писать романы, всегда старайтесь писать структурированные (списками-абзацами тексты). Списки в MediaWiki — это просто «*». Не забывайте о них.
Преформатированный моноширинный текст — просто отступ.
Старайтесь нетривиальные понятия, особенно незнакомые вам, найти ссылку на википедию и вставить (нейросети лажают!).
Это важно, чтобы найти корректный перевод (то, что в википедии, или на худой конец — точно массово гуглится).
Потом конечно сотрите эти инструкции, которые тут курсивом или в блоке цитирования.
Ответы
Если ответы простые, однострочные, используйте простой способ задания ответов списком, типа так (префикс «Правильный ответ:» — это дословно, для правильного ответа, неважно, какой он будет в списке)
- Правильный ответ: тут реально правильный ответ
- неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
Если ответы длинные, многострочные, или там графы, используйте способ задания ответов разделами, Но такое очень редко встречается, например 2011-gre-cs-practice-book.pdf/Q05.
Объяснение
Сначала заполните номер страницы с этим вопросом Исходники — вопрос 12 на тут-номер-страницы-с-вопросом-12 странице книги «2019-gate-computer-science-and-it-practice.pdf»
Если все сделаете правильно, по ссылке выше будет открываться правильная страница в правильном PDFе.
Ну и наконец, вики-разметкой напишите ваше понимание, почему правильный ответ — правильный, а неправильные варианты — неправильны.
Тут тоже могут быть полезны ссылки на википедию, решение вами рекуррентных уравнений в sympy.
Задача зарезервирована: StasFomin 10:34, 25 декабря 2024 (UTC)
Задача «2019-gate-computer-science-and-it-practice.pdf/Q13-alg4»
Вопрос: Q13-alg4-31d68c
Вопрос из «Algorithms Test 4» где-то со страницы 238.
Тут вставьте перевод вопроса.
Используйте возможности разметки, включая формулы и т.п, если будут графы — посмотрите как задать их текстом https://wiki.4intra.net/Graphviz (реально оценю, полезный навык). Если код — теги «code-pascal», «code-c» или «code-python» (не «source lang»).
В IT вообще не принято писать романы, всегда старайтесь писать структурированные (списками-абзацами тексты). Списки в MediaWiki — это просто «*». Не забывайте о них.
Преформатированный моноширинный текст — просто отступ.
Старайтесь нетривиальные понятия, особенно незнакомые вам, найти ссылку на википедию и вставить (нейросети лажают!).
Это важно, чтобы найти корректный перевод (то, что в википедии, или на худой конец — точно массово гуглится).
Потом конечно сотрите эти инструкции, которые тут курсивом или в блоке цитирования.
Ответы
Если ответы простые, однострочные, используйте простой способ задания ответов списком, типа так (префикс «Правильный ответ:» — это дословно, для правильного ответа, неважно, какой он будет в списке)
- Правильный ответ: тут реально правильный ответ
- неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
Если ответы длинные, многострочные, или там графы, используйте способ задания ответов разделами, Но такое очень редко встречается, например 2011-gre-cs-practice-book.pdf/Q05.
Объяснение
Сначала заполните номер страницы с этим вопросом Исходники — вопрос 13 на тут-номер-страницы-с-вопросом-13 странице книги «2019-gate-computer-science-and-it-practice.pdf»
Если все сделаете правильно, по ссылке выше будет открываться правильная страница в правильном PDFе.
Ну и наконец, вики-разметкой напишите ваше понимание, почему правильный ответ — правильный, а неправильные варианты — неправильны.
Тут тоже могут быть полезны ссылки на википедию, решение вами рекуррентных уравнений в sympy.
Задача зарезервирована: StasFomin 10:34, 25 декабря 2024 (UTC)
Задача «2019-gate-computer-science-and-it-practice.pdf/Q14-alg4»
Вопрос: Q14-alg4-31d68c
Вопрос из «Algorithms Test 4» где-то со страницы 238.
Тут вставьте перевод вопроса.
Используйте возможности разметки, включая формулы и т.п, если будут графы — посмотрите как задать их текстом https://wiki.4intra.net/Graphviz (реально оценю, полезный навык). Если код — теги «code-pascal», «code-c» или «code-python» (не «source lang»).
В IT вообще не принято писать романы, всегда старайтесь писать структурированные (списками-абзацами тексты). Списки в MediaWiki — это просто «*». Не забывайте о них.
Преформатированный моноширинный текст — просто отступ.
Старайтесь нетривиальные понятия, особенно незнакомые вам, найти ссылку на википедию и вставить (нейросети лажают!).
Это важно, чтобы найти корректный перевод (то, что в википедии, или на худой конец — точно массово гуглится).
Потом конечно сотрите эти инструкции, которые тут курсивом или в блоке цитирования.
Ответы
Если ответы простые, однострочные, используйте простой способ задания ответов списком, типа так (префикс «Правильный ответ:» — это дословно, для правильного ответа, неважно, какой он будет в списке)
- Правильный ответ: тут реально правильный ответ
- неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
Если ответы длинные, многострочные, или там графы, используйте способ задания ответов разделами, Но такое очень редко встречается, например 2011-gre-cs-practice-book.pdf/Q05.
Объяснение
Сначала заполните номер страницы с этим вопросом Исходники — вопрос 14 на тут-номер-страницы-с-вопросом-14 странице книги «2019-gate-computer-science-and-it-practice.pdf»
Если все сделаете правильно, по ссылке выше будет открываться правильная страница в правильном PDFе.
Ну и наконец, вики-разметкой напишите ваше понимание, почему правильный ответ — правильный, а неправильные варианты — неправильны.
Тут тоже могут быть полезны ссылки на википедию, решение вами рекуррентных уравнений в sympy.
Задача зарезервирована: StasFomin 10:34, 25 декабря 2024 (UTC)
Задача «2019-gate-computer-science-and-it-practice.pdf/Q05-alg4»
Вопрос: Q05-alg4-31d68c
Вопрос из «Algorithms Test 4» где-то со страницы 238.
Тут вставьте перевод вопроса.
Используйте возможности разметки, включая формулы и т.п, если будут графы — посмотрите как задать их текстом https://wiki.4intra.net/Graphviz (реально оценю, полезный навык). Если код — теги «code-pascal», «code-c» или «code-python» (не «source lang»).
В IT вообще не принято писать романы, всегда старайтесь писать структурированные (списками-абзацами тексты). Списки в MediaWiki — это просто «*». Не забывайте о них.
Преформатированный моноширинный текст — просто отступ.
Старайтесь нетривиальные понятия, особенно незнакомые вам, найти ссылку на википедию и вставить (нейросети лажают!).
Это важно, чтобы найти корректный перевод (то, что в википедии, или на худой конец — точно массово гуглится).
Потом конечно сотрите эти инструкции, которые тут курсивом или в блоке цитирования.
Ответы
Если ответы простые, однострочные, используйте простой способ задания ответов списком, типа так (префикс «Правильный ответ:» — это дословно, для правильного ответа, неважно, какой он будет в списке)
- Правильный ответ: тут реально правильный ответ
- неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
Если ответы длинные, многострочные, или там графы, используйте способ задания ответов разделами, Но такое очень редко встречается, например 2011-gre-cs-practice-book.pdf/Q05.
Объяснение
Сначала заполните номер страницы с этим вопросом Исходники — вопрос 5 на тут-номер-страницы-с-вопросом-5 странице книги «2019-gate-computer-science-and-it-practice.pdf»
Если все сделаете правильно, по ссылке выше будет открываться правильная страница в правильном PDFе.
Ну и наконец, вики-разметкой напишите ваше понимание, почему правильный ответ — правильный, а неправильные варианты — неправильны.
Тут тоже могут быть полезны ссылки на википедию, решение вами рекуррентных уравнений в sympy.
Задача зарезервирована: StasFomin 10:34, 25 декабря 2024 (UTC)
Задача «2019-gate-computer-science-and-it-practice.pdf/Q06-alg4»
Вопрос: Q06-alg4-31d68c
Вопрос из «Algorithms Test 4» где-то со страницы 238.
Тут вставьте перевод вопроса.
Используйте возможности разметки, включая формулы и т.п, если будут графы — посмотрите как задать их текстом https://wiki.4intra.net/Graphviz (реально оценю, полезный навык). Если код — теги «code-pascal», «code-c» или «code-python» (не «source lang»).
В IT вообще не принято писать романы, всегда старайтесь писать структурированные (списками-абзацами тексты). Списки в MediaWiki — это просто «*». Не забывайте о них.
Преформатированный моноширинный текст — просто отступ.
Старайтесь нетривиальные понятия, особенно незнакомые вам, найти ссылку на википедию и вставить (нейросети лажают!).
Это важно, чтобы найти корректный перевод (то, что в википедии, или на худой конец — точно массово гуглится).
Потом конечно сотрите эти инструкции, которые тут курсивом или в блоке цитирования.
Ответы
Если ответы простые, однострочные, используйте простой способ задания ответов списком, типа так (префикс «Правильный ответ:» — это дословно, для правильного ответа, неважно, какой он будет в списке)
- Правильный ответ: тут реально правильный ответ
- неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
Если ответы длинные, многострочные, или там графы, используйте способ задания ответов разделами, Но такое очень редко встречается, например 2011-gre-cs-practice-book.pdf/Q05.
Объяснение
Сначала заполните номер страницы с этим вопросом Исходники — вопрос 6 на тут-номер-страницы-с-вопросом-6 странице книги «2019-gate-computer-science-and-it-practice.pdf»
Если все сделаете правильно, по ссылке выше будет открываться правильная страница в правильном PDFе.
Ну и наконец, вики-разметкой напишите ваше понимание, почему правильный ответ — правильный, а неправильные варианты — неправильны.
Тут тоже могут быть полезны ссылки на википедию, решение вами рекуррентных уравнений в sympy.
Задача зарезервирована: StasFomin 10:34, 25 декабря 2024 (UTC)
Задача «2019-gate-computer-science-and-it-practice.pdf/Q07-alg4»
Вопрос: Q07-alg4-31d68c
Вопрос из «Algorithms Test 4» где-то со страницы 238.
Тут вставьте перевод вопроса.
Используйте возможности разметки, включая формулы и т.п, если будут графы — посмотрите как задать их текстом https://wiki.4intra.net/Graphviz (реально оценю, полезный навык). Если код — теги «code-pascal», «code-c» или «code-python» (не «source lang»).
В IT вообще не принято писать романы, всегда старайтесь писать структурированные (списками-абзацами тексты). Списки в MediaWiki — это просто «*». Не забывайте о них.
Преформатированный моноширинный текст — просто отступ.
Старайтесь нетривиальные понятия, особенно незнакомые вам, найти ссылку на википедию и вставить (нейросети лажают!).
Это важно, чтобы найти корректный перевод (то, что в википедии, или на худой конец — точно массово гуглится).
Потом конечно сотрите эти инструкции, которые тут курсивом или в блоке цитирования.
Ответы
Если ответы простые, однострочные, используйте простой способ задания ответов списком, типа так (префикс «Правильный ответ:» — это дословно, для правильного ответа, неважно, какой он будет в списке)
- Правильный ответ: тут реально правильный ответ
- неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
Если ответы длинные, многострочные, или там графы, используйте способ задания ответов разделами, Но такое очень редко встречается, например 2011-gre-cs-practice-book.pdf/Q05.
Объяснение
Сначала заполните номер страницы с этим вопросом Исходники — вопрос 7 на тут-номер-страницы-с-вопросом-7 странице книги «2019-gate-computer-science-and-it-practice.pdf»
Если все сделаете правильно, по ссылке выше будет открываться правильная страница в правильном PDFе.
Ну и наконец, вики-разметкой напишите ваше понимание, почему правильный ответ — правильный, а неправильные варианты — неправильны.
Тут тоже могут быть полезны ссылки на википедию, решение вами рекуррентных уравнений в sympy.
Задача зарезервирована: StasFomin 10:34, 25 декабря 2024 (UTC)
Задача «2019-gate-computer-science-and-it-practice.pdf/Q09-alg4»
Вопрос: Q09-alg4-31d68c
Вопрос из «Algorithms Test 4» где-то со страницы 238.
Тут вставьте перевод вопроса.
Используйте возможности разметки, включая формулы и т.п, если будут графы — посмотрите как задать их текстом https://wiki.4intra.net/Graphviz (реально оценю, полезный навык). Если код — теги «code-pascal», «code-c» или «code-python» (не «source lang»).
В IT вообще не принято писать романы, всегда старайтесь писать структурированные (списками-абзацами тексты). Списки в MediaWiki — это просто «*». Не забывайте о них.
Преформатированный моноширинный текст — просто отступ.
Старайтесь нетривиальные понятия, особенно незнакомые вам, найти ссылку на википедию и вставить (нейросети лажают!).
Это важно, чтобы найти корректный перевод (то, что в википедии, или на худой конец — точно массово гуглится).
Потом конечно сотрите эти инструкции, которые тут курсивом или в блоке цитирования.
Ответы
Если ответы простые, однострочные, используйте простой способ задания ответов списком, типа так (префикс «Правильный ответ:» — это дословно, для правильного ответа, неважно, какой он будет в списке)
- Правильный ответ: тут реально правильный ответ
- неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
Если ответы длинные, многострочные, или там графы, используйте способ задания ответов разделами, Но такое очень редко встречается, например 2011-gre-cs-practice-book.pdf/Q05.
Объяснение
Сначала заполните номер страницы с этим вопросом Исходники — вопрос 9 на тут-номер-страницы-с-вопросом-9 странице книги «2019-gate-computer-science-and-it-practice.pdf»
Если все сделаете правильно, по ссылке выше будет открываться правильная страница в правильном PDFе.
Ну и наконец, вики-разметкой напишите ваше понимание, почему правильный ответ — правильный, а неправильные варианты — неправильны.
Тут тоже могут быть полезны ссылки на википедию, решение вами рекуррентных уравнений в sympy.
Задача зарезервирована: StasFomin 10:34, 25 декабря 2024 (UTC)
Задача «2019-gate-computer-science-and-it-practice.pdf/Q03-alg4»
Вопрос: Q03-alg4-31d68c
Вопрос из «Algorithms Test 4» где-то со страницы 238.
Тут вставьте перевод вопроса.
Используйте возможности разметки, включая формулы и т.п, если будут графы — посмотрите как задать их текстом https://wiki.4intra.net/Graphviz (реально оценю, полезный навык). Если код — теги «code-pascal», «code-c» или «code-python» (не «source lang»).
В IT вообще не принято писать романы, всегда старайтесь писать структурированные (списками-абзацами тексты). Списки в MediaWiki — это просто «*». Не забывайте о них.
Преформатированный моноширинный текст — просто отступ.
Старайтесь нетривиальные понятия, особенно незнакомые вам, найти ссылку на википедию и вставить (нейросети лажают!).
Это важно, чтобы найти корректный перевод (то, что в википедии, или на худой конец — точно массово гуглится).
Потом конечно сотрите эти инструкции, которые тут курсивом или в блоке цитирования.
Ответы
Если ответы простые, однострочные, используйте простой способ задания ответов списком, типа так (префикс «Правильный ответ:» — это дословно, для правильного ответа, неважно, какой он будет в списке)
- Правильный ответ: тут реально правильный ответ
- неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
Если ответы длинные, многострочные, или там графы, используйте способ задания ответов разделами, Но такое очень редко встречается, например 2011-gre-cs-practice-book.pdf/Q05.
Объяснение
Сначала заполните номер страницы с этим вопросом Исходники — вопрос 3 на тут-номер-страницы-с-вопросом-3 странице книги «2019-gate-computer-science-and-it-practice.pdf»
Если все сделаете правильно, по ссылке выше будет открываться правильная страница в правильном PDFе.
Ну и наконец, вики-разметкой напишите ваше понимание, почему правильный ответ — правильный, а неправильные варианты — неправильны.
Тут тоже могут быть полезны ссылки на википедию, решение вами рекуррентных уравнений в sympy.
Задача зарезервирована: StasFomin 10:34, 25 декабря 2024 (UTC)
Задача «2019-gate-computer-science-and-it-practice.pdf/Q04-alg4»
Вопрос: Q04-alg4-31d68c
Вопрос из «Algorithms Test 4» где-то со страницы 238.
Тут вставьте перевод вопроса.
Используйте возможности разметки, включая формулы и т.п, если будут графы — посмотрите как задать их текстом https://wiki.4intra.net/Graphviz (реально оценю, полезный навык). Если код — теги «code-pascal», «code-c» или «code-python» (не «source lang»).
В IT вообще не принято писать романы, всегда старайтесь писать структурированные (списками-абзацами тексты). Списки в MediaWiki — это просто «*». Не забывайте о них.
Преформатированный моноширинный текст — просто отступ.
Старайтесь нетривиальные понятия, особенно незнакомые вам, найти ссылку на википедию и вставить (нейросети лажают!).
Это важно, чтобы найти корректный перевод (то, что в википедии, или на худой конец — точно массово гуглится).
Потом конечно сотрите эти инструкции, которые тут курсивом или в блоке цитирования.
Ответы
Если ответы простые, однострочные, используйте простой способ задания ответов списком, типа так (префикс «Правильный ответ:» — это дословно, для правильного ответа, неважно, какой он будет в списке)
- Правильный ответ: тут реально правильный ответ
- неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
Если ответы длинные, многострочные, или там графы, используйте способ задания ответов разделами, Но такое очень редко встречается, например 2011-gre-cs-practice-book.pdf/Q05.
Объяснение
Сначала заполните номер страницы с этим вопросом Исходники — вопрос 4 на тут-номер-страницы-с-вопросом-4 странице книги «2019-gate-computer-science-and-it-practice.pdf»
Если все сделаете правильно, по ссылке выше будет открываться правильная страница в правильном PDFе.
Ну и наконец, вики-разметкой напишите ваше понимание, почему правильный ответ — правильный, а неправильные варианты — неправильны.
Тут тоже могут быть полезны ссылки на википедию, решение вами рекуррентных уравнений в sympy.
Задача зарезервирована: StasFomin 10:34, 25 декабря 2024 (UTC)
Задача «2019-gate-computer-science-and-it-practice.pdf/Q25-alg3»
Вопрос: Q25-alg3-31d68c
Вопрос из «Algorithms Test 3» где-то со страницы 233.
Тут вставьте перевод вопроса.
Используйте возможности разметки, включая формулы и т.п, если будут графы — посмотрите как задать их текстом https://wiki.4intra.net/Graphviz (реально оценю, полезный навык). Если код — теги «code-pascal», «code-c» или «code-python» (не «source lang»).
В IT вообще не принято писать романы, всегда старайтесь писать структурированные (списками-абзацами тексты). Списки в MediaWiki — это просто «*». Не забывайте о них.
Преформатированный моноширинный текст — просто отступ.
Старайтесь нетривиальные понятия, особенно незнакомые вам, найти ссылку на википедию и вставить (нейросети лажают!).
Это важно, чтобы найти корректный перевод (то, что в википедии, или на худой конец — точно массово гуглится).
Потом конечно сотрите эти инструкции, которые тут курсивом или в блоке цитирования.
Ответы
Если ответы простые, однострочные, используйте простой способ задания ответов списком, типа так (префикс «Правильный ответ:» — это дословно, для правильного ответа, неважно, какой он будет в списке)
- Правильный ответ: тут реально правильный ответ
- неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
Если ответы длинные, многострочные, или там графы, используйте способ задания ответов разделами, Но такое очень редко встречается, например 2011-gre-cs-practice-book.pdf/Q05.
Объяснение
Сначала заполните номер страницы с этим вопросом Исходники — вопрос 25 на тут-номер-страницы-с-вопросом-25 странице книги «2019-gate-computer-science-and-it-practice.pdf»
Если все сделаете правильно, по ссылке выше будет открываться правильная страница в правильном PDFе.
Ну и наконец, вики-разметкой напишите ваше понимание, почему правильный ответ — правильный, а неправильные варианты — неправильны.
Тут тоже могут быть полезны ссылки на википедию, решение вами рекуррентных уравнений в sympy.
Задача зарезервирована: StasFomin 09:52, 25 декабря 2024 (UTC)
Задача «2019-gate-computer-science-and-it-practice.pdf/Q22-alg3»
Вопрос: Q22-alg3-31d68c
Вопрос из «Algorithms Test 3» где-то со страницы 233.
Тут вставьте перевод вопроса.
Используйте возможности разметки, включая формулы и т.п, если будут графы — посмотрите как задать их текстом https://wiki.4intra.net/Graphviz (реально оценю, полезный навык). Если код — теги «code-pascal», «code-c» или «code-python» (не «source lang»).
В IT вообще не принято писать романы, всегда старайтесь писать структурированные (списками-абзацами тексты). Списки в MediaWiki — это просто «*». Не забывайте о них.
Преформатированный моноширинный текст — просто отступ.
Старайтесь нетривиальные понятия, особенно незнакомые вам, найти ссылку на википедию и вставить (нейросети лажают!).
Это важно, чтобы найти корректный перевод (то, что в википедии, или на худой конец — точно массово гуглится).
Потом конечно сотрите эти инструкции, которые тут курсивом или в блоке цитирования.
Ответы
Если ответы простые, однострочные, используйте простой способ задания ответов списком, типа так (префикс «Правильный ответ:» — это дословно, для правильного ответа, неважно, какой он будет в списке)
- Правильный ответ: тут реально правильный ответ
- неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
Если ответы длинные, многострочные, или там графы, используйте способ задания ответов разделами, Но такое очень редко встречается, например 2011-gre-cs-practice-book.pdf/Q05.
Объяснение
Сначала заполните номер страницы с этим вопросом Исходники — вопрос 22 на тут-номер-страницы-с-вопросом-22 странице книги «2019-gate-computer-science-and-it-practice.pdf»
Если все сделаете правильно, по ссылке выше будет открываться правильная страница в правильном PDFе.
Ну и наконец, вики-разметкой напишите ваше понимание, почему правильный ответ — правильный, а неправильные варианты — неправильны.
Тут тоже могут быть полезны ссылки на википедию, решение вами рекуррентных уравнений в sympy.
Задача зарезервирована: StasFomin 09:52, 25 декабря 2024 (UTC)
Задача «2019-gate-computer-science-and-it-practice.pdf/Q23-alg3»
Вопрос: Q23-alg3-31d68c
Вопрос из «Algorithms Test 3» где-то со страницы 233.
Тут вставьте перевод вопроса.
Используйте возможности разметки, включая формулы и т.п, если будут графы — посмотрите как задать их текстом https://wiki.4intra.net/Graphviz (реально оценю, полезный навык). Если код — теги «code-pascal», «code-c» или «code-python» (не «source lang»).
В IT вообще не принято писать романы, всегда старайтесь писать структурированные (списками-абзацами тексты). Списки в MediaWiki — это просто «*». Не забывайте о них.
Преформатированный моноширинный текст — просто отступ.
Старайтесь нетривиальные понятия, особенно незнакомые вам, найти ссылку на википедию и вставить (нейросети лажают!).
Это важно, чтобы найти корректный перевод (то, что в википедии, или на худой конец — точно массово гуглится).
Потом конечно сотрите эти инструкции, которые тут курсивом или в блоке цитирования.
Ответы
Если ответы простые, однострочные, используйте простой способ задания ответов списком, типа так (префикс «Правильный ответ:» — это дословно, для правильного ответа, неважно, какой он будет в списке)
- Правильный ответ: тут реально правильный ответ
- неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
Если ответы длинные, многострочные, или там графы, используйте способ задания ответов разделами, Но такое очень редко встречается, например 2011-gre-cs-practice-book.pdf/Q05.
Объяснение
Сначала заполните номер страницы с этим вопросом Исходники — вопрос 23 на тут-номер-страницы-с-вопросом-23 странице книги «2019-gate-computer-science-and-it-practice.pdf»
Если все сделаете правильно, по ссылке выше будет открываться правильная страница в правильном PDFе.
Ну и наконец, вики-разметкой напишите ваше понимание, почему правильный ответ — правильный, а неправильные варианты — неправильны.
Тут тоже могут быть полезны ссылки на википедию, решение вами рекуррентных уравнений в sympy.
Задача зарезервирована: StasFomin 09:52, 25 декабря 2024 (UTC)
Задача «2019-gate-computer-science-and-it-practice.pdf/Q24-alg3»
Вопрос: Q24-alg3-31d68c
Вопрос из «Algorithms Test 3» где-то со страницы 233.
Тут вставьте перевод вопроса.
Используйте возможности разметки, включая формулы и т.п, если будут графы — посмотрите как задать их текстом https://wiki.4intra.net/Graphviz (реально оценю, полезный навык). Если код — теги «code-pascal», «code-c» или «code-python» (не «source lang»).
В IT вообще не принято писать романы, всегда старайтесь писать структурированные (списками-абзацами тексты). Списки в MediaWiki — это просто «*». Не забывайте о них.
Преформатированный моноширинный текст — просто отступ.
Старайтесь нетривиальные понятия, особенно незнакомые вам, найти ссылку на википедию и вставить (нейросети лажают!).
Это важно, чтобы найти корректный перевод (то, что в википедии, или на худой конец — точно массово гуглится).
Потом конечно сотрите эти инструкции, которые тут курсивом или в блоке цитирования.
Ответы
Если ответы простые, однострочные, используйте простой способ задания ответов списком, типа так (префикс «Правильный ответ:» — это дословно, для правильного ответа, неважно, какой он будет в списке)
- Правильный ответ: тут реально правильный ответ
- неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
Если ответы длинные, многострочные, или там графы, используйте способ задания ответов разделами, Но такое очень редко встречается, например 2011-gre-cs-practice-book.pdf/Q05.
Объяснение
Сначала заполните номер страницы с этим вопросом Исходники — вопрос 24 на тут-номер-страницы-с-вопросом-24 странице книги «2019-gate-computer-science-and-it-practice.pdf»
Если все сделаете правильно, по ссылке выше будет открываться правильная страница в правильном PDFе.
Ну и наконец, вики-разметкой напишите ваше понимание, почему правильный ответ — правильный, а неправильные варианты — неправильны.
Тут тоже могут быть полезны ссылки на википедию, решение вами рекуррентных уравнений в sympy.
Задача зарезервирована: StasFomin 09:52, 25 декабря 2024 (UTC)
Задача «2019-gate-computer-science-and-it-practice.pdf/Q16-alg3»
Вопрос: Q16-alg3-31d68c
Вопрос из «Algorithms Test 3» где-то со страницы 233.
Тут вставьте перевод вопроса.
Используйте возможности разметки, включая формулы и т.п, если будут графы — посмотрите как задать их текстом https://wiki.4intra.net/Graphviz (реально оценю, полезный навык). Если код — теги «code-pascal», «code-c» или «code-python» (не «source lang»).
В IT вообще не принято писать романы, всегда старайтесь писать структурированные (списками-абзацами тексты). Списки в MediaWiki — это просто «*». Не забывайте о них.
Преформатированный моноширинный текст — просто отступ.
Старайтесь нетривиальные понятия, особенно незнакомые вам, найти ссылку на википедию и вставить (нейросети лажают!).
Это важно, чтобы найти корректный перевод (то, что в википедии, или на худой конец — точно массово гуглится).
Потом конечно сотрите эти инструкции, которые тут курсивом или в блоке цитирования.
Ответы
Если ответы простые, однострочные, используйте простой способ задания ответов списком, типа так (префикс «Правильный ответ:» — это дословно, для правильного ответа, неважно, какой он будет в списке)
- Правильный ответ: тут реально правильный ответ
- неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
Если ответы длинные, многострочные, или там графы, используйте способ задания ответов разделами, Но такое очень редко встречается, например 2011-gre-cs-practice-book.pdf/Q05.
Объяснение
Сначала заполните номер страницы с этим вопросом Исходники — вопрос 16 на тут-номер-страницы-с-вопросом-16 странице книги «2019-gate-computer-science-and-it-practice.pdf»
Если все сделаете правильно, по ссылке выше будет открываться правильная страница в правильном PDFе.
Ну и наконец, вики-разметкой напишите ваше понимание, почему правильный ответ — правильный, а неправильные варианты — неправильны.
Тут тоже могут быть полезны ссылки на википедию, решение вами рекуррентных уравнений в sympy.
Задача зарезервирована: StasFomin 09:52, 25 декабря 2024 (UTC)
Задача «2019-gate-computer-science-and-it-practice.pdf/Q18-alg3»
Вопрос: Q18-alg3-31d68c
Вопрос из «Algorithms Test 3» где-то со страницы 233.
Тут вставьте перевод вопроса.
Используйте возможности разметки, включая формулы и т.п, если будут графы — посмотрите как задать их текстом https://wiki.4intra.net/Graphviz (реально оценю, полезный навык). Если код — теги «code-pascal», «code-c» или «code-python» (не «source lang»).
В IT вообще не принято писать романы, всегда старайтесь писать структурированные (списками-абзацами тексты). Списки в MediaWiki — это просто «*». Не забывайте о них.
Преформатированный моноширинный текст — просто отступ.
Старайтесь нетривиальные понятия, особенно незнакомые вам, найти ссылку на википедию и вставить (нейросети лажают!).
Это важно, чтобы найти корректный перевод (то, что в википедии, или на худой конец — точно массово гуглится).
Потом конечно сотрите эти инструкции, которые тут курсивом или в блоке цитирования.
Ответы
Если ответы простые, однострочные, используйте простой способ задания ответов списком, типа так (префикс «Правильный ответ:» — это дословно, для правильного ответа, неважно, какой он будет в списке)
- Правильный ответ: тут реально правильный ответ
- неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
Если ответы длинные, многострочные, или там графы, используйте способ задания ответов разделами, Но такое очень редко встречается, например 2011-gre-cs-practice-book.pdf/Q05.
Объяснение
Сначала заполните номер страницы с этим вопросом Исходники — вопрос 18 на тут-номер-страницы-с-вопросом-18 странице книги «2019-gate-computer-science-and-it-practice.pdf»
Если все сделаете правильно, по ссылке выше будет открываться правильная страница в правильном PDFе.
Ну и наконец, вики-разметкой напишите ваше понимание, почему правильный ответ — правильный, а неправильные варианты — неправильны.
Тут тоже могут быть полезны ссылки на википедию, решение вами рекуррентных уравнений в sympy.
Задача зарезервирована: StasFomin 09:52, 25 декабря 2024 (UTC)
Задача «2019-gate-computer-science-and-it-practice.pdf/Q19-alg3»
Вопрос: Q19-alg3-31d68c
Вопрос из «Algorithms Test 3» где-то со страницы 233.
Тут вставьте перевод вопроса.
Используйте возможности разметки, включая формулы и т.п, если будут графы — посмотрите как задать их текстом https://wiki.4intra.net/Graphviz (реально оценю, полезный навык). Если код — теги «code-pascal», «code-c» или «code-python» (не «source lang»).
В IT вообще не принято писать романы, всегда старайтесь писать структурированные (списками-абзацами тексты). Списки в MediaWiki — это просто «*». Не забывайте о них.
Преформатированный моноширинный текст — просто отступ.
Старайтесь нетривиальные понятия, особенно незнакомые вам, найти ссылку на википедию и вставить (нейросети лажают!).
Это важно, чтобы найти корректный перевод (то, что в википедии, или на худой конец — точно массово гуглится).
Потом конечно сотрите эти инструкции, которые тут курсивом или в блоке цитирования.
Ответы
Если ответы простые, однострочные, используйте простой способ задания ответов списком, типа так (префикс «Правильный ответ:» — это дословно, для правильного ответа, неважно, какой он будет в списке)
- Правильный ответ: тут реально правильный ответ
- неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
Если ответы длинные, многострочные, или там графы, используйте способ задания ответов разделами, Но такое очень редко встречается, например 2011-gre-cs-practice-book.pdf/Q05.
Объяснение
Сначала заполните номер страницы с этим вопросом Исходники — вопрос 19 на тут-номер-страницы-с-вопросом-19 странице книги «2019-gate-computer-science-and-it-practice.pdf»
Если все сделаете правильно, по ссылке выше будет открываться правильная страница в правильном PDFе.
Ну и наконец, вики-разметкой напишите ваше понимание, почему правильный ответ — правильный, а неправильные варианты — неправильны.
Тут тоже могут быть полезны ссылки на википедию, решение вами рекуррентных уравнений в sympy.
Задача зарезервирована: StasFomin 09:52, 25 декабря 2024 (UTC)
Задача «2019-gate-computer-science-and-it-practice.pdf/Q20-alg3»
Вопрос: Q20-alg3-31d68c
Вопрос из «Algorithms Test 3» где-то со страницы 233.
Тут вставьте перевод вопроса.
Используйте возможности разметки, включая формулы и т.п, если будут графы — посмотрите как задать их текстом https://wiki.4intra.net/Graphviz (реально оценю, полезный навык). Если код — теги «code-pascal», «code-c» или «code-python» (не «source lang»).
В IT вообще не принято писать романы, всегда старайтесь писать структурированные (списками-абзацами тексты). Списки в MediaWiki — это просто «*». Не забывайте о них.
Преформатированный моноширинный текст — просто отступ.
Старайтесь нетривиальные понятия, особенно незнакомые вам, найти ссылку на википедию и вставить (нейросети лажают!).
Это важно, чтобы найти корректный перевод (то, что в википедии, или на худой конец — точно массово гуглится).
Потом конечно сотрите эти инструкции, которые тут курсивом или в блоке цитирования.
Ответы
Если ответы простые, однострочные, используйте простой способ задания ответов списком, типа так (префикс «Правильный ответ:» — это дословно, для правильного ответа, неважно, какой он будет в списке)
- Правильный ответ: тут реально правильный ответ
- неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
Если ответы длинные, многострочные, или там графы, используйте способ задания ответов разделами, Но такое очень редко встречается, например 2011-gre-cs-practice-book.pdf/Q05.
Объяснение
Сначала заполните номер страницы с этим вопросом Исходники — вопрос 20 на тут-номер-страницы-с-вопросом-20 странице книги «2019-gate-computer-science-and-it-practice.pdf»
Если все сделаете правильно, по ссылке выше будет открываться правильная страница в правильном PDFе.
Ну и наконец, вики-разметкой напишите ваше понимание, почему правильный ответ — правильный, а неправильные варианты — неправильны.
Тут тоже могут быть полезны ссылки на википедию, решение вами рекуррентных уравнений в sympy.
Задача зарезервирована: StasFomin 09:52, 25 декабря 2024 (UTC)
Задача «2019-gate-computer-science-and-it-practice.pdf/Q14-alg3»
Вопрос: Q14-alg3-31d68c
Вопрос из «Algorithms Test 3» где-то со страницы 233.
Тут вставьте перевод вопроса.
Используйте возможности разметки, включая формулы и т.п, если будут графы — посмотрите как задать их текстом https://wiki.4intra.net/Graphviz (реально оценю, полезный навык). Если код — теги «code-pascal», «code-c» или «code-python» (не «source lang»).
В IT вообще не принято писать романы, всегда старайтесь писать структурированные (списками-абзацами тексты). Списки в MediaWiki — это просто «*». Не забывайте о них.
Преформатированный моноширинный текст — просто отступ.
Старайтесь нетривиальные понятия, особенно незнакомые вам, найти ссылку на википедию и вставить (нейросети лажают!).
Это важно, чтобы найти корректный перевод (то, что в википедии, или на худой конец — точно массово гуглится).
Потом конечно сотрите эти инструкции, которые тут курсивом или в блоке цитирования.
Ответы
Если ответы простые, однострочные, используйте простой способ задания ответов списком, типа так (префикс «Правильный ответ:» — это дословно, для правильного ответа, неважно, какой он будет в списке)
- Правильный ответ: тут реально правильный ответ
- неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
Если ответы длинные, многострочные, или там графы, используйте способ задания ответов разделами, Но такое очень редко встречается, например 2011-gre-cs-practice-book.pdf/Q05.
Объяснение
Сначала заполните номер страницы с этим вопросом Исходники — вопрос 14 на тут-номер-страницы-с-вопросом-14 странице книги «2019-gate-computer-science-and-it-practice.pdf»
Если все сделаете правильно, по ссылке выше будет открываться правильная страница в правильном PDFе.
Ну и наконец, вики-разметкой напишите ваше понимание, почему правильный ответ — правильный, а неправильные варианты — неправильны.
Тут тоже могут быть полезны ссылки на википедию, решение вами рекуррентных уравнений в sympy.
Задача зарезервирована: StasFomin 09:52, 25 декабря 2024 (UTC)
Задача «2019-gate-computer-science-and-it-practice.pdf/Q15-alg3»
Вопрос: Q15-alg3-31d68c
Вопрос из «Algorithms Test 3» где-то со страницы 233.
Тут вставьте перевод вопроса.
Используйте возможности разметки, включая формулы и т.п, если будут графы — посмотрите как задать их текстом https://wiki.4intra.net/Graphviz (реально оценю, полезный навык). Если код — теги «code-pascal», «code-c» или «code-python» (не «source lang»).
В IT вообще не принято писать романы, всегда старайтесь писать структурированные (списками-абзацами тексты). Списки в MediaWiki — это просто «*». Не забывайте о них.
Преформатированный моноширинный текст — просто отступ.
Старайтесь нетривиальные понятия, особенно незнакомые вам, найти ссылку на википедию и вставить (нейросети лажают!).
Это важно, чтобы найти корректный перевод (то, что в википедии, или на худой конец — точно массово гуглится).
Потом конечно сотрите эти инструкции, которые тут курсивом или в блоке цитирования.
Ответы
Если ответы простые, однострочные, используйте простой способ задания ответов списком, типа так (префикс «Правильный ответ:» — это дословно, для правильного ответа, неважно, какой он будет в списке)
- Правильный ответ: тут реально правильный ответ
- неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
Если ответы длинные, многострочные, или там графы, используйте способ задания ответов разделами, Но такое очень редко встречается, например 2011-gre-cs-practice-book.pdf/Q05.
Объяснение
Сначала заполните номер страницы с этим вопросом Исходники — вопрос 15 на тут-номер-страницы-с-вопросом-15 странице книги «2019-gate-computer-science-and-it-practice.pdf»
Если все сделаете правильно, по ссылке выше будет открываться правильная страница в правильном PDFе.
Ну и наконец, вики-разметкой напишите ваше понимание, почему правильный ответ — правильный, а неправильные варианты — неправильны.
Тут тоже могут быть полезны ссылки на википедию, решение вами рекуррентных уравнений в sympy.
Задача зарезервирована: StasFomin 09:52, 25 декабря 2024 (UTC)
Задача «2019-gate-computer-science-and-it-practice.pdf/Q11-alg3»
Вопрос: Q11-alg3-31d68c
Вопрос из «Algorithms Test 3» где-то со страницы 233.
Тут вставьте перевод вопроса.
Используйте возможности разметки, включая формулы и т.п, если будут графы — посмотрите как задать их текстом https://wiki.4intra.net/Graphviz (реально оценю, полезный навык). Если код — теги «code-pascal», «code-c» или «code-python» (не «source lang»).
В IT вообще не принято писать романы, всегда старайтесь писать структурированные (списками-абзацами тексты). Списки в MediaWiki — это просто «*». Не забывайте о них.
Преформатированный моноширинный текст — просто отступ.
Старайтесь нетривиальные понятия, особенно незнакомые вам, найти ссылку на википедию и вставить (нейросети лажают!).
Это важно, чтобы найти корректный перевод (то, что в википедии, или на худой конец — точно массово гуглится).
Потом конечно сотрите эти инструкции, которые тут курсивом или в блоке цитирования.
Ответы
Если ответы простые, однострочные, используйте простой способ задания ответов списком, типа так (префикс «Правильный ответ:» — это дословно, для правильного ответа, неважно, какой он будет в списке)
- Правильный ответ: тут реально правильный ответ
- неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
Если ответы длинные, многострочные, или там графы, используйте способ задания ответов разделами, Но такое очень редко встречается, например 2011-gre-cs-practice-book.pdf/Q05.
Объяснение
Сначала заполните номер страницы с этим вопросом Исходники — вопрос 11 на тут-номер-страницы-с-вопросом-11 странице книги «2019-gate-computer-science-and-it-practice.pdf»
Если все сделаете правильно, по ссылке выше будет открываться правильная страница в правильном PDFе.
Ну и наконец, вики-разметкой напишите ваше понимание, почему правильный ответ — правильный, а неправильные варианты — неправильны.
Тут тоже могут быть полезны ссылки на википедию, решение вами рекуррентных уравнений в sympy.
Задача зарезервирована: StasFomin 09:52, 25 декабря 2024 (UTC)
Задача «2019-gate-computer-science-and-it-practice.pdf/Q08-alg3»
Вопрос: Q08-alg3-31d68c
Вопрос из «Algorithms Test 3» где-то со страницы 233.
Тут вставьте перевод вопроса.
Используйте возможности разметки, включая формулы и т.п, если будут графы — посмотрите как задать их текстом https://wiki.4intra.net/Graphviz (реально оценю, полезный навык). Если код — теги «code-pascal», «code-c» или «code-python» (не «source lang»).
В IT вообще не принято писать романы, всегда старайтесь писать структурированные (списками-абзацами тексты). Списки в MediaWiki — это просто «*». Не забывайте о них.
Преформатированный моноширинный текст — просто отступ.
Старайтесь нетривиальные понятия, особенно незнакомые вам, найти ссылку на википедию и вставить (нейросети лажают!).
Это важно, чтобы найти корректный перевод (то, что в википедии, или на худой конец — точно массово гуглится).
Потом конечно сотрите эти инструкции, которые тут курсивом или в блоке цитирования.
Ответы
Если ответы простые, однострочные, используйте простой способ задания ответов списком, типа так (префикс «Правильный ответ:» — это дословно, для правильного ответа, неважно, какой он будет в списке)
- Правильный ответ: тут реально правильный ответ
- неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
Если ответы длинные, многострочные, или там графы, используйте способ задания ответов разделами, Но такое очень редко встречается, например 2011-gre-cs-practice-book.pdf/Q05.
Объяснение
Сначала заполните номер страницы с этим вопросом Исходники — вопрос 8 на тут-номер-страницы-с-вопросом-8 странице книги «2019-gate-computer-science-and-it-practice.pdf»
Если все сделаете правильно, по ссылке выше будет открываться правильная страница в правильном PDFе.
Ну и наконец, вики-разметкой напишите ваше понимание, почему правильный ответ — правильный, а неправильные варианты — неправильны.
Тут тоже могут быть полезны ссылки на википедию, решение вами рекуррентных уравнений в sympy.
Задача зарезервирована: StasFomin 09:52, 25 декабря 2024 (UTC)
Задача «2019-gate-computer-science-and-it-practice.pdf/Q09-alg3»
Вопрос: Q09-alg3-31d68c
Вопрос из «Algorithms Test 3» где-то со страницы 233.
Тут вставьте перевод вопроса.
Используйте возможности разметки, включая формулы и т.п, если будут графы — посмотрите как задать их текстом https://wiki.4intra.net/Graphviz (реально оценю, полезный навык). Если код — теги «code-pascal», «code-c» или «code-python» (не «source lang»).
В IT вообще не принято писать романы, всегда старайтесь писать структурированные (списками-абзацами тексты). Списки в MediaWiki — это просто «*». Не забывайте о них.
Преформатированный моноширинный текст — просто отступ.
Старайтесь нетривиальные понятия, особенно незнакомые вам, найти ссылку на википедию и вставить (нейросети лажают!).
Это важно, чтобы найти корректный перевод (то, что в википедии, или на худой конец — точно массово гуглится).
Потом конечно сотрите эти инструкции, которые тут курсивом или в блоке цитирования.
Ответы
Если ответы простые, однострочные, используйте простой способ задания ответов списком, типа так (префикс «Правильный ответ:» — это дословно, для правильного ответа, неважно, какой он будет в списке)
- Правильный ответ: тут реально правильный ответ
- неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
Если ответы длинные, многострочные, или там графы, используйте способ задания ответов разделами, Но такое очень редко встречается, например 2011-gre-cs-practice-book.pdf/Q05.
Объяснение
Сначала заполните номер страницы с этим вопросом Исходники — вопрос 9 на тут-номер-страницы-с-вопросом-9 странице книги «2019-gate-computer-science-and-it-practice.pdf»
Если все сделаете правильно, по ссылке выше будет открываться правильная страница в правильном PDFе.
Ну и наконец, вики-разметкой напишите ваше понимание, почему правильный ответ — правильный, а неправильные варианты — неправильны.
Тут тоже могут быть полезны ссылки на википедию, решение вами рекуррентных уравнений в sympy.
Задача зарезервирована: StasFomin 09:52, 25 декабря 2024 (UTC)
Задача «2019-gate-computer-science-and-it-practice.pdf/Q04-alg3»
Вопрос: Q04-alg3-31d68c
Вопрос из «Algorithms Test 3» где-то со страницы 233.
Тут вставьте перевод вопроса.
Используйте возможности разметки, включая формулы и т.п, если будут графы — посмотрите как задать их текстом https://wiki.4intra.net/Graphviz (реально оценю, полезный навык). Если код — теги «code-pascal», «code-c» или «code-python» (не «source lang»).
В IT вообще не принято писать романы, всегда старайтесь писать структурированные (списками-абзацами тексты). Списки в MediaWiki — это просто «*». Не забывайте о них.
Преформатированный моноширинный текст — просто отступ.
Старайтесь нетривиальные понятия, особенно незнакомые вам, найти ссылку на википедию и вставить (нейросети лажают!).
Это важно, чтобы найти корректный перевод (то, что в википедии, или на худой конец — точно массово гуглится).
Потом конечно сотрите эти инструкции, которые тут курсивом или в блоке цитирования.
Ответы
Если ответы простые, однострочные, используйте простой способ задания ответов списком, типа так (префикс «Правильный ответ:» — это дословно, для правильного ответа, неважно, какой он будет в списке)
- Правильный ответ: тут реально правильный ответ
- неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
Если ответы длинные, многострочные, или там графы, используйте способ задания ответов разделами, Но такое очень редко встречается, например 2011-gre-cs-practice-book.pdf/Q05.
Объяснение
Сначала заполните номер страницы с этим вопросом Исходники — вопрос 4 на тут-номер-страницы-с-вопросом-4 странице книги «2019-gate-computer-science-and-it-practice.pdf»
Если все сделаете правильно, по ссылке выше будет открываться правильная страница в правильном PDFе.
Ну и наконец, вики-разметкой напишите ваше понимание, почему правильный ответ — правильный, а неправильные варианты — неправильны.
Тут тоже могут быть полезны ссылки на википедию, решение вами рекуррентных уравнений в sympy.
Задача зарезервирована: StasFomin 09:52, 25 декабря 2024 (UTC)
Задача «2019-gate-computer-science-and-it-practice.pdf/Q06-alg3»
Вопрос: Q06-alg3-31d68c
Вопрос из «Algorithms Test 3» где-то со страницы 233.
Тут вставьте перевод вопроса.
Используйте возможности разметки, включая формулы и т.п, если будут графы — посмотрите как задать их текстом https://wiki.4intra.net/Graphviz (реально оценю, полезный навык). Если код — теги «code-pascal», «code-c» или «code-python» (не «source lang»).
В IT вообще не принято писать романы, всегда старайтесь писать структурированные (списками-абзацами тексты). Списки в MediaWiki — это просто «*». Не забывайте о них.
Преформатированный моноширинный текст — просто отступ.
Старайтесь нетривиальные понятия, особенно незнакомые вам, найти ссылку на википедию и вставить (нейросети лажают!).
Это важно, чтобы найти корректный перевод (то, что в википедии, или на худой конец — точно массово гуглится).
Потом конечно сотрите эти инструкции, которые тут курсивом или в блоке цитирования.
Ответы
Если ответы простые, однострочные, используйте простой способ задания ответов списком, типа так (префикс «Правильный ответ:» — это дословно, для правильного ответа, неважно, какой он будет в списке)
- Правильный ответ: тут реально правильный ответ
- неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
Если ответы длинные, многострочные, или там графы, используйте способ задания ответов разделами, Но такое очень редко встречается, например 2011-gre-cs-practice-book.pdf/Q05.
Объяснение
Сначала заполните номер страницы с этим вопросом Исходники — вопрос 6 на тут-номер-страницы-с-вопросом-6 странице книги «2019-gate-computer-science-and-it-practice.pdf»
Если все сделаете правильно, по ссылке выше будет открываться правильная страница в правильном PDFе.
Ну и наконец, вики-разметкой напишите ваше понимание, почему правильный ответ — правильный, а неправильные варианты — неправильны.
Тут тоже могут быть полезны ссылки на википедию, решение вами рекуррентных уравнений в sympy.
Задача зарезервирована: StasFomin 09:52, 25 декабря 2024 (UTC)
Задача «2019-gate-computer-science-and-it-practice.pdf/Q01-alg3»
Вопрос: Q01-alg3-31d68c
Вопрос из «Algorithms Test 3» где-то со страницы 233.
Тут вставьте перевод вопроса.
Используйте возможности разметки, включая формулы и т.п, если будут графы — посмотрите как задать их текстом https://wiki.4intra.net/Graphviz (реально оценю, полезный навык). Если код — теги «code-pascal», «code-c» или «code-python» (не «source lang»).
В IT вообще не принято писать романы, всегда старайтесь писать структурированные (списками-абзацами тексты). Списки в MediaWiki — это просто «*». Не забывайте о них.
Преформатированный моноширинный текст — просто отступ.
Старайтесь нетривиальные понятия, особенно незнакомые вам, найти ссылку на википедию и вставить (нейросети лажают!).
Это важно, чтобы найти корректный перевод (то, что в википедии, или на худой конец — точно массово гуглится).
Потом конечно сотрите эти инструкции, которые тут курсивом или в блоке цитирования.
Ответы
Если ответы простые, однострочные, используйте простой способ задания ответов списком, типа так (префикс «Правильный ответ:» — это дословно, для правильного ответа, неважно, какой он будет в списке)
- Правильный ответ: тут реально правильный ответ
- неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
Если ответы длинные, многострочные, или там графы, используйте способ задания ответов разделами, Но такое очень редко встречается, например 2011-gre-cs-practice-book.pdf/Q05.
Объяснение
Сначала заполните номер страницы с этим вопросом Исходники — вопрос 1 на тут-номер-страницы-с-вопросом-1 странице книги «2019-gate-computer-science-and-it-practice.pdf»
Если все сделаете правильно, по ссылке выше будет открываться правильная страница в правильном PDFе.
Ну и наконец, вики-разметкой напишите ваше понимание, почему правильный ответ — правильный, а неправильные варианты — неправильны.
Тут тоже могут быть полезны ссылки на википедию, решение вами рекуррентных уравнений в sympy.
Задача зарезервирована: StasFomin 09:52, 25 декабря 2024 (UTC)
Задача «2019-gate-computer-science-and-it-practice.pdf/Q03-alg3»
Вопрос: Q03-alg3-31d68c
Вопрос из «Algorithms Test 3» где-то со страницы 233.
Тут вставьте перевод вопроса.
Используйте возможности разметки, включая формулы и т.п, если будут графы — посмотрите как задать их текстом https://wiki.4intra.net/Graphviz (реально оценю, полезный навык). Если код — теги «code-pascal», «code-c» или «code-python» (не «source lang»).
В IT вообще не принято писать романы, всегда старайтесь писать структурированные (списками-абзацами тексты). Списки в MediaWiki — это просто «*». Не забывайте о них.
Преформатированный моноширинный текст — просто отступ.
Старайтесь нетривиальные понятия, особенно незнакомые вам, найти ссылку на википедию и вставить (нейросети лажают!).
Это важно, чтобы найти корректный перевод (то, что в википедии, или на худой конец — точно массово гуглится).
Потом конечно сотрите эти инструкции, которые тут курсивом или в блоке цитирования.
Ответы
Если ответы простые, однострочные, используйте простой способ задания ответов списком, типа так (префикс «Правильный ответ:» — это дословно, для правильного ответа, неважно, какой он будет в списке)
- Правильный ответ: тут реально правильный ответ
- неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
Если ответы длинные, многострочные, или там графы, используйте способ задания ответов разделами, Но такое очень редко встречается, например 2011-gre-cs-practice-book.pdf/Q05.
Объяснение
Сначала заполните номер страницы с этим вопросом Исходники — вопрос 3 на тут-номер-страницы-с-вопросом-3 странице книги «2019-gate-computer-science-and-it-practice.pdf»
Если все сделаете правильно, по ссылке выше будет открываться правильная страница в правильном PDFе.
Ну и наконец, вики-разметкой напишите ваше понимание, почему правильный ответ — правильный, а неправильные варианты — неправильны.
Тут тоже могут быть полезны ссылки на википедию, решение вами рекуррентных уравнений в sympy.
Задача зарезервирована: StasFomin 09:52, 25 декабря 2024 (UTC)
Задача «2019-gate-computer-science-and-it-practice.pdf/Q33-alg2»
Вопрос: Q33-alg2-31d68c
Вопрос из «Algorithms Test 2» где-то со страницы 226.
Тут вставьте перевод вопроса.
Используйте возможности разметки, включая формулы и т.п, если будут графы — посмотрите как задать их текстом https://wiki.4intra.net/Graphviz (реально оценю, полезный навык). Если код — теги «code-pascal», «code-c» или «code-python» (не «source lang»).
В IT вообще не принято писать романы, всегда старайтесь писать структурированные (списками-абзацами тексты). Списки в MediaWiki — это просто «*». Не забывайте о них.
Преформатированный моноширинный текст — просто отступ.
Старайтесь нетривиальные понятия, особенно незнакомые вам, найти ссылку на википедию и вставить (нейросети лажают!).
Это важно, чтобы найти корректный перевод (то, что в википедии, или на худой конец — точно массово гуглится).
Потом конечно сотрите эти инструкции, которые тут курсивом или в блоке цитирования.
Ответы
Если ответы простые, однострочные, используйте простой способ задания ответов списком, типа так (префикс «Правильный ответ:» — это дословно, для правильного ответа, неважно, какой он будет в списке)
- Правильный ответ: тут реально правильный ответ
- неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
Если ответы длинные, многострочные, или там графы, используйте способ задания ответов разделами, Но такое очень редко встречается, например 2011-gre-cs-practice-book.pdf/Q05.
Объяснение
Сначала заполните номер страницы с этим вопросом Исходники — вопрос 33 на тут-номер-страницы-с-вопросом-33 странице книги «2019-gate-computer-science-and-it-practice.pdf»
Если все сделаете правильно, по ссылке выше будет открываться правильная страница в правильном PDFе.
Ну и наконец, вики-разметкой напишите ваше понимание, почему правильный ответ — правильный, а неправильные варианты — неправильны.
Тут тоже могут быть полезны ссылки на википедию, решение вами рекуррентных уравнений в sympy.
Задача зарезервирована: StasFomin 00:31, 25 декабря 2024 (UTC)
Задача «2019-gate-computer-science-and-it-practice.pdf/Q34-alg2»
Вопрос: Q34-alg2-31d68c
Вопрос из «Algorithms Test 2» где-то со страницы 226.
Тут вставьте перевод вопроса.
Используйте возможности разметки, включая формулы и т.п, если будут графы — посмотрите как задать их текстом https://wiki.4intra.net/Graphviz (реально оценю, полезный навык). Если код — теги «code-pascal», «code-c» или «code-python» (не «source lang»).
В IT вообще не принято писать романы, всегда старайтесь писать структурированные (списками-абзацами тексты). Списки в MediaWiki — это просто «*». Не забывайте о них.
Преформатированный моноширинный текст — просто отступ.
Старайтесь нетривиальные понятия, особенно незнакомые вам, найти ссылку на википедию и вставить (нейросети лажают!).
Это важно, чтобы найти корректный перевод (то, что в википедии, или на худой конец — точно массово гуглится).
Потом конечно сотрите эти инструкции, которые тут курсивом или в блоке цитирования.
Ответы
Если ответы простые, однострочные, используйте простой способ задания ответов списком, типа так (префикс «Правильный ответ:» — это дословно, для правильного ответа, неважно, какой он будет в списке)
- Правильный ответ: тут реально правильный ответ
- неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
Если ответы длинные, многострочные, или там графы, используйте способ задания ответов разделами, Но такое очень редко встречается, например 2011-gre-cs-practice-book.pdf/Q05.
Объяснение
Сначала заполните номер страницы с этим вопросом Исходники — вопрос 34 на тут-номер-страницы-с-вопросом-34 странице книги «2019-gate-computer-science-and-it-practice.pdf»
Если все сделаете правильно, по ссылке выше будет открываться правильная страница в правильном PDFе.
Ну и наконец, вики-разметкой напишите ваше понимание, почему правильный ответ — правильный, а неправильные варианты — неправильны.
Тут тоже могут быть полезны ссылки на википедию, решение вами рекуррентных уравнений в sympy.
Задача зарезервирована: StasFomin 00:31, 25 декабря 2024 (UTC)
Задача «2019-gate-computer-science-and-it-practice.pdf/Q35-alg2»
Вопрос: Q35-alg2-31d68c
Вопрос из «Algorithms Test 2» где-то со страницы 226.
Тут вставьте перевод вопроса.
Используйте возможности разметки, включая формулы и т.п, если будут графы — посмотрите как задать их текстом https://wiki.4intra.net/Graphviz (реально оценю, полезный навык). Если код — теги «code-pascal», «code-c» или «code-python» (не «source lang»).
В IT вообще не принято писать романы, всегда старайтесь писать структурированные (списками-абзацами тексты). Списки в MediaWiki — это просто «*». Не забывайте о них.
Преформатированный моноширинный текст — просто отступ.
Старайтесь нетривиальные понятия, особенно незнакомые вам, найти ссылку на википедию и вставить (нейросети лажают!).
Это важно, чтобы найти корректный перевод (то, что в википедии, или на худой конец — точно массово гуглится).
Потом конечно сотрите эти инструкции, которые тут курсивом или в блоке цитирования.
Ответы
Если ответы простые, однострочные, используйте простой способ задания ответов списком, типа так (префикс «Правильный ответ:» — это дословно, для правильного ответа, неважно, какой он будет в списке)
- Правильный ответ: тут реально правильный ответ
- неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
Если ответы длинные, многострочные, или там графы, используйте способ задания ответов разделами, Но такое очень редко встречается, например 2011-gre-cs-practice-book.pdf/Q05.
Объяснение
Сначала заполните номер страницы с этим вопросом Исходники — вопрос 35 на тут-номер-страницы-с-вопросом-35 странице книги «2019-gate-computer-science-and-it-practice.pdf»
Если все сделаете правильно, по ссылке выше будет открываться правильная страница в правильном PDFе.
Ну и наконец, вики-разметкой напишите ваше понимание, почему правильный ответ — правильный, а неправильные варианты — неправильны.
Тут тоже могут быть полезны ссылки на википедию, решение вами рекуррентных уравнений в sympy.
Задача зарезервирована: StasFomin 00:31, 25 декабря 2024 (UTC)
Задача «2019-gate-computer-science-and-it-practice.pdf/Q30-alg2»
Вопрос: Q30-alg2-31d68c
Вопрос из «Algorithms Test 2» где-то со страницы 226.
Тут вставьте перевод вопроса.
Используйте возможности разметки, включая формулы и т.п, если будут графы — посмотрите как задать их текстом https://wiki.4intra.net/Graphviz (реально оценю, полезный навык). Если код — теги «code-pascal», «code-c» или «code-python» (не «source lang»).
В IT вообще не принято писать романы, всегда старайтесь писать структурированные (списками-абзацами тексты). Списки в MediaWiki — это просто «*». Не забывайте о них.
Преформатированный моноширинный текст — просто отступ.
Старайтесь нетривиальные понятия, особенно незнакомые вам, найти ссылку на википедию и вставить (нейросети лажают!).
Это важно, чтобы найти корректный перевод (то, что в википедии, или на худой конец — точно массово гуглится).
Потом конечно сотрите эти инструкции, которые тут курсивом или в блоке цитирования.
Ответы
Если ответы простые, однострочные, используйте простой способ задания ответов списком, типа так (префикс «Правильный ответ:» — это дословно, для правильного ответа, неважно, какой он будет в списке)
- Правильный ответ: тут реально правильный ответ
- неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
Если ответы длинные, многострочные, или там графы, используйте способ задания ответов разделами, Но такое очень редко встречается, например 2011-gre-cs-practice-book.pdf/Q05.
Объяснение
Сначала заполните номер страницы с этим вопросом Исходники — вопрос 30 на тут-номер-страницы-с-вопросом-30 странице книги «2019-gate-computer-science-and-it-practice.pdf»
Если все сделаете правильно, по ссылке выше будет открываться правильная страница в правильном PDFе.
Ну и наконец, вики-разметкой напишите ваше понимание, почему правильный ответ — правильный, а неправильные варианты — неправильны.
Тут тоже могут быть полезны ссылки на википедию, решение вами рекуррентных уравнений в sympy.
Задача зарезервирована: StasFomin 00:31, 25 декабря 2024 (UTC)
Задача «2019-gate-computer-science-and-it-practice.pdf/Q31-alg2»
Вопрос: Q31-alg2-31d68c
Вопрос из «Algorithms Test 2» где-то со страницы 226.
Тут вставьте перевод вопроса.
Используйте возможности разметки, включая формулы и т.п, если будут графы — посмотрите как задать их текстом https://wiki.4intra.net/Graphviz (реально оценю, полезный навык). Если код — теги «code-pascal», «code-c» или «code-python» (не «source lang»).
В IT вообще не принято писать романы, всегда старайтесь писать структурированные (списками-абзацами тексты). Списки в MediaWiki — это просто «*». Не забывайте о них.
Преформатированный моноширинный текст — просто отступ.
Старайтесь нетривиальные понятия, особенно незнакомые вам, найти ссылку на википедию и вставить (нейросети лажают!).
Это важно, чтобы найти корректный перевод (то, что в википедии, или на худой конец — точно массово гуглится).
Потом конечно сотрите эти инструкции, которые тут курсивом или в блоке цитирования.
Ответы
Если ответы простые, однострочные, используйте простой способ задания ответов списком, типа так (префикс «Правильный ответ:» — это дословно, для правильного ответа, неважно, какой он будет в списке)
- Правильный ответ: тут реально правильный ответ
- неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
Если ответы длинные, многострочные, или там графы, используйте способ задания ответов разделами, Но такое очень редко встречается, например 2011-gre-cs-practice-book.pdf/Q05.
Объяснение
Сначала заполните номер страницы с этим вопросом Исходники — вопрос 31 на тут-номер-страницы-с-вопросом-31 странице книги «2019-gate-computer-science-and-it-practice.pdf»
Если все сделаете правильно, по ссылке выше будет открываться правильная страница в правильном PDFе.
Ну и наконец, вики-разметкой напишите ваше понимание, почему правильный ответ — правильный, а неправильные варианты — неправильны.
Тут тоже могут быть полезны ссылки на википедию, решение вами рекуррентных уравнений в sympy.
Задача зарезервирована: StasFomin 00:31, 25 декабря 2024 (UTC)
Задача «2019-gate-computer-science-and-it-practice.pdf/Q32-alg2»
Вопрос: Q32-alg2-31d68c
Вопрос из «Algorithms Test 2» где-то со страницы 226.
Тут вставьте перевод вопроса.
Используйте возможности разметки, включая формулы и т.п, если будут графы — посмотрите как задать их текстом https://wiki.4intra.net/Graphviz (реально оценю, полезный навык). Если код — теги «code-pascal», «code-c» или «code-python» (не «source lang»).
В IT вообще не принято писать романы, всегда старайтесь писать структурированные (списками-абзацами тексты). Списки в MediaWiki — это просто «*». Не забывайте о них.
Преформатированный моноширинный текст — просто отступ.
Старайтесь нетривиальные понятия, особенно незнакомые вам, найти ссылку на википедию и вставить (нейросети лажают!).
Это важно, чтобы найти корректный перевод (то, что в википедии, или на худой конец — точно массово гуглится).
Потом конечно сотрите эти инструкции, которые тут курсивом или в блоке цитирования.
Ответы
Если ответы простые, однострочные, используйте простой способ задания ответов списком, типа так (префикс «Правильный ответ:» — это дословно, для правильного ответа, неважно, какой он будет в списке)
- Правильный ответ: тут реально правильный ответ
- неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
Если ответы длинные, многострочные, или там графы, используйте способ задания ответов разделами, Но такое очень редко встречается, например 2011-gre-cs-practice-book.pdf/Q05.
Объяснение
Сначала заполните номер страницы с этим вопросом Исходники — вопрос 32 на тут-номер-страницы-с-вопросом-32 странице книги «2019-gate-computer-science-and-it-practice.pdf»
Если все сделаете правильно, по ссылке выше будет открываться правильная страница в правильном PDFе.
Ну и наконец, вики-разметкой напишите ваше понимание, почему правильный ответ — правильный, а неправильные варианты — неправильны.
Тут тоже могут быть полезны ссылки на википедию, решение вами рекуррентных уравнений в sympy.
Задача зарезервирована: StasFomin 00:31, 25 декабря 2024 (UTC)
Задача «2019-gate-computer-science-and-it-practice.pdf/Q29-alg2»
Вопрос: Q29-alg2-31d68c
Вопрос из «Algorithms Test 2» где-то со страницы 226.
Тут вставьте перевод вопроса.
Используйте возможности разметки, включая формулы и т.п, если будут графы — посмотрите как задать их текстом https://wiki.4intra.net/Graphviz (реально оценю, полезный навык). Если код — теги «code-pascal», «code-c» или «code-python» (не «source lang»).
В IT вообще не принято писать романы, всегда старайтесь писать структурированные (списками-абзацами тексты). Списки в MediaWiki — это просто «*». Не забывайте о них.
Преформатированный моноширинный текст — просто отступ.
Старайтесь нетривиальные понятия, особенно незнакомые вам, найти ссылку на википедию и вставить (нейросети лажают!).
Это важно, чтобы найти корректный перевод (то, что в википедии, или на худой конец — точно массово гуглится).
Потом конечно сотрите эти инструкции, которые тут курсивом или в блоке цитирования.
Ответы
Если ответы простые, однострочные, используйте простой способ задания ответов списком, типа так (префикс «Правильный ответ:» — это дословно, для правильного ответа, неважно, какой он будет в списке)
- Правильный ответ: тут реально правильный ответ
- неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
Если ответы длинные, многострочные, или там графы, используйте способ задания ответов разделами, Но такое очень редко встречается, например 2011-gre-cs-practice-book.pdf/Q05.
Объяснение
Сначала заполните номер страницы с этим вопросом Исходники — вопрос 29 на тут-номер-страницы-с-вопросом-29 странице книги «2019-gate-computer-science-and-it-practice.pdf»
Если все сделаете правильно, по ссылке выше будет открываться правильная страница в правильном PDFе.
Ну и наконец, вики-разметкой напишите ваше понимание, почему правильный ответ — правильный, а неправильные варианты — неправильны.
Тут тоже могут быть полезны ссылки на википедию, решение вами рекуррентных уравнений в sympy.
Задача зарезервирована: StasFomin 00:31, 25 декабря 2024 (UTC)
Задача «2019-gate-computer-science-and-it-practice.pdf/Q24-alg2»
Вопрос: Q24-alg2-31d68c
Вопрос из «Algorithms Test 2» где-то со страницы 226.
Тут вставьте перевод вопроса.
Используйте возможности разметки, включая формулы и т.п, если будут графы — посмотрите как задать их текстом https://wiki.4intra.net/Graphviz (реально оценю, полезный навык). Если код — теги «code-pascal», «code-c» или «code-python» (не «source lang»).
В IT вообще не принято писать романы, всегда старайтесь писать структурированные (списками-абзацами тексты). Списки в MediaWiki — это просто «*». Не забывайте о них.
Преформатированный моноширинный текст — просто отступ.
Старайтесь нетривиальные понятия, особенно незнакомые вам, найти ссылку на википедию и вставить (нейросети лажают!).
Это важно, чтобы найти корректный перевод (то, что в википедии, или на худой конец — точно массово гуглится).
Потом конечно сотрите эти инструкции, которые тут курсивом или в блоке цитирования.
Ответы
Если ответы простые, однострочные, используйте простой способ задания ответов списком, типа так (префикс «Правильный ответ:» — это дословно, для правильного ответа, неважно, какой он будет в списке)
- Правильный ответ: тут реально правильный ответ
- неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
Если ответы длинные, многострочные, или там графы, используйте способ задания ответов разделами, Но такое очень редко встречается, например 2011-gre-cs-practice-book.pdf/Q05.
Объяснение
Сначала заполните номер страницы с этим вопросом Исходники — вопрос 24 на тут-номер-страницы-с-вопросом-24 странице книги «2019-gate-computer-science-and-it-practice.pdf»
Если все сделаете правильно, по ссылке выше будет открываться правильная страница в правильном PDFе.
Ну и наконец, вики-разметкой напишите ваше понимание, почему правильный ответ — правильный, а неправильные варианты — неправильны.
Тут тоже могут быть полезны ссылки на википедию, решение вами рекуррентных уравнений в sympy.
Задача зарезервирована: StasFomin 00:31, 25 декабря 2024 (UTC)
Задача «2019-gate-computer-science-and-it-practice.pdf/Q25-alg2»
Вопрос: Q25-alg2-31d68c
Вопрос из «Algorithms Test 2» где-то со страницы 226.
Тут вставьте перевод вопроса.
Используйте возможности разметки, включая формулы и т.п, если будут графы — посмотрите как задать их текстом https://wiki.4intra.net/Graphviz (реально оценю, полезный навык). Если код — теги «code-pascal», «code-c» или «code-python» (не «source lang»).
В IT вообще не принято писать романы, всегда старайтесь писать структурированные (списками-абзацами тексты). Списки в MediaWiki — это просто «*». Не забывайте о них.
Преформатированный моноширинный текст — просто отступ.
Старайтесь нетривиальные понятия, особенно незнакомые вам, найти ссылку на википедию и вставить (нейросети лажают!).
Это важно, чтобы найти корректный перевод (то, что в википедии, или на худой конец — точно массово гуглится).
Потом конечно сотрите эти инструкции, которые тут курсивом или в блоке цитирования.
Ответы
Если ответы простые, однострочные, используйте простой способ задания ответов списком, типа так (префикс «Правильный ответ:» — это дословно, для правильного ответа, неважно, какой он будет в списке)
- Правильный ответ: тут реально правильный ответ
- неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
Если ответы длинные, многострочные, или там графы, используйте способ задания ответов разделами, Но такое очень редко встречается, например 2011-gre-cs-practice-book.pdf/Q05.
Объяснение
Сначала заполните номер страницы с этим вопросом Исходники — вопрос 25 на тут-номер-страницы-с-вопросом-25 странице книги «2019-gate-computer-science-and-it-practice.pdf»
Если все сделаете правильно, по ссылке выше будет открываться правильная страница в правильном PDFе.
Ну и наконец, вики-разметкой напишите ваше понимание, почему правильный ответ — правильный, а неправильные варианты — неправильны.
Тут тоже могут быть полезны ссылки на википедию, решение вами рекуррентных уравнений в sympy.
Задача зарезервирована: StasFomin 00:31, 25 декабря 2024 (UTC)
Задача «2019-gate-computer-science-and-it-practice.pdf/Q26-alg2»
Вопрос: Q26-alg2-31d68c
Вопрос из «Algorithms Test 2» где-то со страницы 226.
Тут вставьте перевод вопроса.
Используйте возможности разметки, включая формулы и т.п, если будут графы — посмотрите как задать их текстом https://wiki.4intra.net/Graphviz (реально оценю, полезный навык). Если код — теги «code-pascal», «code-c» или «code-python» (не «source lang»).
В IT вообще не принято писать романы, всегда старайтесь писать структурированные (списками-абзацами тексты). Списки в MediaWiki — это просто «*». Не забывайте о них.
Преформатированный моноширинный текст — просто отступ.
Старайтесь нетривиальные понятия, особенно незнакомые вам, найти ссылку на википедию и вставить (нейросети лажают!).
Это важно, чтобы найти корректный перевод (то, что в википедии, или на худой конец — точно массово гуглится).
Потом конечно сотрите эти инструкции, которые тут курсивом или в блоке цитирования.
Ответы
Если ответы простые, однострочные, используйте простой способ задания ответов списком, типа так (префикс «Правильный ответ:» — это дословно, для правильного ответа, неважно, какой он будет в списке)
- Правильный ответ: тут реально правильный ответ
- неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
Если ответы длинные, многострочные, или там графы, используйте способ задания ответов разделами, Но такое очень редко встречается, например 2011-gre-cs-practice-book.pdf/Q05.
Объяснение
Сначала заполните номер страницы с этим вопросом Исходники — вопрос 26 на тут-номер-страницы-с-вопросом-26 странице книги «2019-gate-computer-science-and-it-practice.pdf»
Если все сделаете правильно, по ссылке выше будет открываться правильная страница в правильном PDFе.
Ну и наконец, вики-разметкой напишите ваше понимание, почему правильный ответ — правильный, а неправильные варианты — неправильны.
Тут тоже могут быть полезны ссылки на википедию, решение вами рекуррентных уравнений в sympy.
Задача зарезервирована: StasFomin 00:31, 25 декабря 2024 (UTC)
Задача «2019-gate-computer-science-and-it-practice.pdf/Q27-alg2»
Вопрос: Q27-alg2-31d68c
Вопрос из «Algorithms Test 2» где-то со страницы 226.
Тут вставьте перевод вопроса.
Используйте возможности разметки, включая формулы и т.п, если будут графы — посмотрите как задать их текстом https://wiki.4intra.net/Graphviz (реально оценю, полезный навык). Если код — теги «code-pascal», «code-c» или «code-python» (не «source lang»).
В IT вообще не принято писать романы, всегда старайтесь писать структурированные (списками-абзацами тексты). Списки в MediaWiki — это просто «*». Не забывайте о них.
Преформатированный моноширинный текст — просто отступ.
Старайтесь нетривиальные понятия, особенно незнакомые вам, найти ссылку на википедию и вставить (нейросети лажают!).
Это важно, чтобы найти корректный перевод (то, что в википедии, или на худой конец — точно массово гуглится).
Потом конечно сотрите эти инструкции, которые тут курсивом или в блоке цитирования.
Ответы
Если ответы простые, однострочные, используйте простой способ задания ответов списком, типа так (префикс «Правильный ответ:» — это дословно, для правильного ответа, неважно, какой он будет в списке)
- Правильный ответ: тут реально правильный ответ
- неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
Если ответы длинные, многострочные, или там графы, используйте способ задания ответов разделами, Но такое очень редко встречается, например 2011-gre-cs-practice-book.pdf/Q05.
Объяснение
Сначала заполните номер страницы с этим вопросом Исходники — вопрос 27 на тут-номер-страницы-с-вопросом-27 странице книги «2019-gate-computer-science-and-it-practice.pdf»
Если все сделаете правильно, по ссылке выше будет открываться правильная страница в правильном PDFе.
Ну и наконец, вики-разметкой напишите ваше понимание, почему правильный ответ — правильный, а неправильные варианты — неправильны.
Тут тоже могут быть полезны ссылки на википедию, решение вами рекуррентных уравнений в sympy.
Задача зарезервирована: StasFomin 00:31, 25 декабря 2024 (UTC)
Задача «2019-gate-computer-science-and-it-practice.pdf/Q28-alg2»
Вопрос: Q28-alg2-31d68c
Вопрос из «Algorithms Test 2» где-то со страницы 226.
Тут вставьте перевод вопроса.
Используйте возможности разметки, включая формулы и т.п, если будут графы — посмотрите как задать их текстом https://wiki.4intra.net/Graphviz (реально оценю, полезный навык). Если код — теги «code-pascal», «code-c» или «code-python» (не «source lang»).
В IT вообще не принято писать романы, всегда старайтесь писать структурированные (списками-абзацами тексты). Списки в MediaWiki — это просто «*». Не забывайте о них.
Преформатированный моноширинный текст — просто отступ.
Старайтесь нетривиальные понятия, особенно незнакомые вам, найти ссылку на википедию и вставить (нейросети лажают!).
Это важно, чтобы найти корректный перевод (то, что в википедии, или на худой конец — точно массово гуглится).
Потом конечно сотрите эти инструкции, которые тут курсивом или в блоке цитирования.
Ответы
Если ответы простые, однострочные, используйте простой способ задания ответов списком, типа так (префикс «Правильный ответ:» — это дословно, для правильного ответа, неважно, какой он будет в списке)
- Правильный ответ: тут реально правильный ответ
- неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
Если ответы длинные, многострочные, или там графы, используйте способ задания ответов разделами, Но такое очень редко встречается, например 2011-gre-cs-practice-book.pdf/Q05.
Объяснение
Сначала заполните номер страницы с этим вопросом Исходники — вопрос 28 на тут-номер-страницы-с-вопросом-28 странице книги «2019-gate-computer-science-and-it-practice.pdf»
Если все сделаете правильно, по ссылке выше будет открываться правильная страница в правильном PDFе.
Ну и наконец, вики-разметкой напишите ваше понимание, почему правильный ответ — правильный, а неправильные варианты — неправильны.
Тут тоже могут быть полезны ссылки на википедию, решение вами рекуррентных уравнений в sympy.
Задача зарезервирована: StasFomin 00:31, 25 декабря 2024 (UTC)
Задача «2019-gate-computer-science-and-it-practice.pdf/Q20-alg2»
Вопрос: Q20-alg2-31d68c
Вопрос из «Algorithms Test 2» где-то со страницы 226.
Тут вставьте перевод вопроса.
Используйте возможности разметки, включая формулы и т.п, если будут графы — посмотрите как задать их текстом https://wiki.4intra.net/Graphviz (реально оценю, полезный навык). Если код — теги «code-pascal», «code-c» или «code-python» (не «source lang»).
В IT вообще не принято писать романы, всегда старайтесь писать структурированные (списками-абзацами тексты). Списки в MediaWiki — это просто «*». Не забывайте о них.
Преформатированный моноширинный текст — просто отступ.
Старайтесь нетривиальные понятия, особенно незнакомые вам, найти ссылку на википедию и вставить (нейросети лажают!).
Это важно, чтобы найти корректный перевод (то, что в википедии, или на худой конец — точно массово гуглится).
Потом конечно сотрите эти инструкции, которые тут курсивом или в блоке цитирования.
Ответы
Если ответы простые, однострочные, используйте простой способ задания ответов списком, типа так (префикс «Правильный ответ:» — это дословно, для правильного ответа, неважно, какой он будет в списке)
- Правильный ответ: тут реально правильный ответ
- неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
Если ответы длинные, многострочные, или там графы, используйте способ задания ответов разделами, Но такое очень редко встречается, например 2011-gre-cs-practice-book.pdf/Q05.
Объяснение
Сначала заполните номер страницы с этим вопросом Исходники — вопрос 20 на тут-номер-страницы-с-вопросом-20 странице книги «2019-gate-computer-science-and-it-practice.pdf»
Если все сделаете правильно, по ссылке выше будет открываться правильная страница в правильном PDFе.
Ну и наконец, вики-разметкой напишите ваше понимание, почему правильный ответ — правильный, а неправильные варианты — неправильны.
Тут тоже могут быть полезны ссылки на википедию, решение вами рекуррентных уравнений в sympy.
Задача зарезервирована: StasFomin 00:31, 25 декабря 2024 (UTC)
Задача «2019-gate-computer-science-and-it-practice.pdf/Q21-alg2»
Вопрос: Q21-alg2-31d68c
Вопрос из «Algorithms Test 2» где-то со страницы 226.
Тут вставьте перевод вопроса.
Используйте возможности разметки, включая формулы и т.п, если будут графы — посмотрите как задать их текстом https://wiki.4intra.net/Graphviz (реально оценю, полезный навык). Если код — теги «code-pascal», «code-c» или «code-python» (не «source lang»).
В IT вообще не принято писать романы, всегда старайтесь писать структурированные (списками-абзацами тексты). Списки в MediaWiki — это просто «*». Не забывайте о них.
Преформатированный моноширинный текст — просто отступ.
Старайтесь нетривиальные понятия, особенно незнакомые вам, найти ссылку на википедию и вставить (нейросети лажают!).
Это важно, чтобы найти корректный перевод (то, что в википедии, или на худой конец — точно массово гуглится).
Потом конечно сотрите эти инструкции, которые тут курсивом или в блоке цитирования.
Ответы
Если ответы простые, однострочные, используйте простой способ задания ответов списком, типа так (префикс «Правильный ответ:» — это дословно, для правильного ответа, неважно, какой он будет в списке)
- Правильный ответ: тут реально правильный ответ
- неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
Если ответы длинные, многострочные, или там графы, используйте способ задания ответов разделами, Но такое очень редко встречается, например 2011-gre-cs-practice-book.pdf/Q05.
Объяснение
Сначала заполните номер страницы с этим вопросом Исходники — вопрос 21 на тут-номер-страницы-с-вопросом-21 странице книги «2019-gate-computer-science-and-it-practice.pdf»
Если все сделаете правильно, по ссылке выше будет открываться правильная страница в правильном PDFе.
Ну и наконец, вики-разметкой напишите ваше понимание, почему правильный ответ — правильный, а неправильные варианты — неправильны.
Тут тоже могут быть полезны ссылки на википедию, решение вами рекуррентных уравнений в sympy.
Задача зарезервирована: StasFomin 00:31, 25 декабря 2024 (UTC)
Задача «2019-gate-computer-science-and-it-practice.pdf/Q22-alg2»
Вопрос: Q22-alg2-31d68c
Вопрос из «Algorithms Test 2» где-то со страницы 226.
Тут вставьте перевод вопроса.
Используйте возможности разметки, включая формулы и т.п, если будут графы — посмотрите как задать их текстом https://wiki.4intra.net/Graphviz (реально оценю, полезный навык). Если код — теги «code-pascal», «code-c» или «code-python» (не «source lang»).
В IT вообще не принято писать романы, всегда старайтесь писать структурированные (списками-абзацами тексты). Списки в MediaWiki — это просто «*». Не забывайте о них.
Преформатированный моноширинный текст — просто отступ.
Старайтесь нетривиальные понятия, особенно незнакомые вам, найти ссылку на википедию и вставить (нейросети лажают!).
Это важно, чтобы найти корректный перевод (то, что в википедии, или на худой конец — точно массово гуглится).
Потом конечно сотрите эти инструкции, которые тут курсивом или в блоке цитирования.
Ответы
Если ответы простые, однострочные, используйте простой способ задания ответов списком, типа так (префикс «Правильный ответ:» — это дословно, для правильного ответа, неважно, какой он будет в списке)
- Правильный ответ: тут реально правильный ответ
- неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
Если ответы длинные, многострочные, или там графы, используйте способ задания ответов разделами, Но такое очень редко встречается, например 2011-gre-cs-practice-book.pdf/Q05.
Объяснение
Сначала заполните номер страницы с этим вопросом Исходники — вопрос 22 на тут-номер-страницы-с-вопросом-22 странице книги «2019-gate-computer-science-and-it-practice.pdf»
Если все сделаете правильно, по ссылке выше будет открываться правильная страница в правильном PDFе.
Ну и наконец, вики-разметкой напишите ваше понимание, почему правильный ответ — правильный, а неправильные варианты — неправильны.
Тут тоже могут быть полезны ссылки на википедию, решение вами рекуррентных уравнений в sympy.
Задача зарезервирована: StasFomin 00:31, 25 декабря 2024 (UTC)
Задача «2019-gate-computer-science-and-it-practice.pdf/Q23-alg2»
Вопрос: Q23-alg2-31d68c
Вопрос из «Algorithms Test 2» где-то со страницы 226.
Тут вставьте перевод вопроса.
Используйте возможности разметки, включая формулы и т.п, если будут графы — посмотрите как задать их текстом https://wiki.4intra.net/Graphviz (реально оценю, полезный навык). Если код — теги «code-pascal», «code-c» или «code-python» (не «source lang»).
В IT вообще не принято писать романы, всегда старайтесь писать структурированные (списками-абзацами тексты). Списки в MediaWiki — это просто «*». Не забывайте о них.
Преформатированный моноширинный текст — просто отступ.
Старайтесь нетривиальные понятия, особенно незнакомые вам, найти ссылку на википедию и вставить (нейросети лажают!).
Это важно, чтобы найти корректный перевод (то, что в википедии, или на худой конец — точно массово гуглится).
Потом конечно сотрите эти инструкции, которые тут курсивом или в блоке цитирования.
Ответы
Если ответы простые, однострочные, используйте простой способ задания ответов списком, типа так (префикс «Правильный ответ:» — это дословно, для правильного ответа, неважно, какой он будет в списке)
- Правильный ответ: тут реально правильный ответ
- неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
Если ответы длинные, многострочные, или там графы, используйте способ задания ответов разделами, Но такое очень редко встречается, например 2011-gre-cs-practice-book.pdf/Q05.
Объяснение
Сначала заполните номер страницы с этим вопросом Исходники — вопрос 23 на тут-номер-страницы-с-вопросом-23 странице книги «2019-gate-computer-science-and-it-practice.pdf»
Если все сделаете правильно, по ссылке выше будет открываться правильная страница в правильном PDFе.
Ну и наконец, вики-разметкой напишите ваше понимание, почему правильный ответ — правильный, а неправильные варианты — неправильны.
Тут тоже могут быть полезны ссылки на википедию, решение вами рекуррентных уравнений в sympy.
Задача зарезервирована: StasFomin 00:31, 25 декабря 2024 (UTC)
Задача «2019-gate-computer-science-and-it-practice.pdf/Q17-alg2»
Вопрос: Q17-alg2-31d68c
Вопрос из «Algorithms Test 2» где-то со страницы 226.
Тут вставьте перевод вопроса.
Используйте возможности разметки, включая формулы и т.п, если будут графы — посмотрите как задать их текстом https://wiki.4intra.net/Graphviz (реально оценю, полезный навык). Если код — теги «code-pascal», «code-c» или «code-python» (не «source lang»).
В IT вообще не принято писать романы, всегда старайтесь писать структурированные (списками-абзацами тексты). Списки в MediaWiki — это просто «*». Не забывайте о них.
Преформатированный моноширинный текст — просто отступ.
Старайтесь нетривиальные понятия, особенно незнакомые вам, найти ссылку на википедию и вставить (нейросети лажают!).
Это важно, чтобы найти корректный перевод (то, что в википедии, или на худой конец — точно массово гуглится).
Потом конечно сотрите эти инструкции, которые тут курсивом или в блоке цитирования.
Ответы
Если ответы простые, однострочные, используйте простой способ задания ответов списком, типа так (префикс «Правильный ответ:» — это дословно, для правильного ответа, неважно, какой он будет в списке)
- Правильный ответ: тут реально правильный ответ
- неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
Если ответы длинные, многострочные, или там графы, используйте способ задания ответов разделами, Но такое очень редко встречается, например 2011-gre-cs-practice-book.pdf/Q05.
Объяснение
Сначала заполните номер страницы с этим вопросом Исходники — вопрос 17 на тут-номер-страницы-с-вопросом-17 странице книги «2019-gate-computer-science-and-it-practice.pdf»
Если все сделаете правильно, по ссылке выше будет открываться правильная страница в правильном PDFе.
Ну и наконец, вики-разметкой напишите ваше понимание, почему правильный ответ — правильный, а неправильные варианты — неправильны.
Тут тоже могут быть полезны ссылки на википедию, решение вами рекуррентных уравнений в sympy.
Задача зарезервирована: StasFomin 00:31, 25 декабря 2024 (UTC)
Задача «2019-gate-computer-science-and-it-practice.pdf/Q18-alg2»
Вопрос: Q18-alg2-31d68c
Вопрос из «Algorithms Test 2» где-то со страницы 226.
Тут вставьте перевод вопроса.
Используйте возможности разметки, включая формулы и т.п, если будут графы — посмотрите как задать их текстом https://wiki.4intra.net/Graphviz (реально оценю, полезный навык). Если код — теги «code-pascal», «code-c» или «code-python» (не «source lang»).
В IT вообще не принято писать романы, всегда старайтесь писать структурированные (списками-абзацами тексты). Списки в MediaWiki — это просто «*». Не забывайте о них.
Преформатированный моноширинный текст — просто отступ.
Старайтесь нетривиальные понятия, особенно незнакомые вам, найти ссылку на википедию и вставить (нейросети лажают!).
Это важно, чтобы найти корректный перевод (то, что в википедии, или на худой конец — точно массово гуглится).
Потом конечно сотрите эти инструкции, которые тут курсивом или в блоке цитирования.
Ответы
Если ответы простые, однострочные, используйте простой способ задания ответов списком, типа так (префикс «Правильный ответ:» — это дословно, для правильного ответа, неважно, какой он будет в списке)
- Правильный ответ: тут реально правильный ответ
- неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
Если ответы длинные, многострочные, или там графы, используйте способ задания ответов разделами, Но такое очень редко встречается, например 2011-gre-cs-practice-book.pdf/Q05.
Объяснение
Сначала заполните номер страницы с этим вопросом Исходники — вопрос 18 на тут-номер-страницы-с-вопросом-18 странице книги «2019-gate-computer-science-and-it-practice.pdf»
Если все сделаете правильно, по ссылке выше будет открываться правильная страница в правильном PDFе.
Ну и наконец, вики-разметкой напишите ваше понимание, почему правильный ответ — правильный, а неправильные варианты — неправильны.
Тут тоже могут быть полезны ссылки на википедию, решение вами рекуррентных уравнений в sympy.
Задача зарезервирована: StasFomin 00:31, 25 декабря 2024 (UTC)
Задача «2019-gate-computer-science-and-it-practice.pdf/Q19-alg2»
Вопрос: Q19-alg2-31d68c
Вопрос из «Algorithms Test 2» где-то со страницы 226.
Тут вставьте перевод вопроса.
Используйте возможности разметки, включая формулы и т.п, если будут графы — посмотрите как задать их текстом https://wiki.4intra.net/Graphviz (реально оценю, полезный навык). Если код — теги «code-pascal», «code-c» или «code-python» (не «source lang»).
В IT вообще не принято писать романы, всегда старайтесь писать структурированные (списками-абзацами тексты). Списки в MediaWiki — это просто «*». Не забывайте о них.
Преформатированный моноширинный текст — просто отступ.
Старайтесь нетривиальные понятия, особенно незнакомые вам, найти ссылку на википедию и вставить (нейросети лажают!).
Это важно, чтобы найти корректный перевод (то, что в википедии, или на худой конец — точно массово гуглится).
Потом конечно сотрите эти инструкции, которые тут курсивом или в блоке цитирования.
Ответы
Если ответы простые, однострочные, используйте простой способ задания ответов списком, типа так (префикс «Правильный ответ:» — это дословно, для правильного ответа, неважно, какой он будет в списке)
- Правильный ответ: тут реально правильный ответ
- неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
Если ответы длинные, многострочные, или там графы, используйте способ задания ответов разделами, Но такое очень редко встречается, например 2011-gre-cs-practice-book.pdf/Q05.
Объяснение
Сначала заполните номер страницы с этим вопросом Исходники — вопрос 19 на тут-номер-страницы-с-вопросом-19 странице книги «2019-gate-computer-science-and-it-practice.pdf»
Если все сделаете правильно, по ссылке выше будет открываться правильная страница в правильном PDFе.
Ну и наконец, вики-разметкой напишите ваше понимание, почему правильный ответ — правильный, а неправильные варианты — неправильны.
Тут тоже могут быть полезны ссылки на википедию, решение вами рекуррентных уравнений в sympy.
Задача зарезервирована: StasFomin 00:31, 25 декабря 2024 (UTC)
Задача «2019-gate-computer-science-and-it-practice.pdf/Q16-alg2»
Вопрос: Q16-alg2-31d68c
Вопрос из «Algorithms Test 2» где-то со страницы 226.
Тут вставьте перевод вопроса.
Используйте возможности разметки, включая формулы и т.п, если будут графы — посмотрите как задать их текстом https://wiki.4intra.net/Graphviz (реально оценю, полезный навык). Если код — теги «code-pascal», «code-c» или «code-python» (не «source lang»).
В IT вообще не принято писать романы, всегда старайтесь писать структурированные (списками-абзацами тексты). Списки в MediaWiki — это просто «*». Не забывайте о них.
Преформатированный моноширинный текст — просто отступ.
Старайтесь нетривиальные понятия, особенно незнакомые вам, найти ссылку на википедию и вставить (нейросети лажают!).
Это важно, чтобы найти корректный перевод (то, что в википедии, или на худой конец — точно массово гуглится).
Потом конечно сотрите эти инструкции, которые тут курсивом или в блоке цитирования.
Ответы
Если ответы простые, однострочные, используйте простой способ задания ответов списком, типа так (префикс «Правильный ответ:» — это дословно, для правильного ответа, неважно, какой он будет в списке)
- Правильный ответ: тут реально правильный ответ
- неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
Если ответы длинные, многострочные, или там графы, используйте способ задания ответов разделами, Но такое очень редко встречается, например 2011-gre-cs-practice-book.pdf/Q05.
Объяснение
Сначала заполните номер страницы с этим вопросом Исходники — вопрос 16 на тут-номер-страницы-с-вопросом-16 странице книги «2019-gate-computer-science-and-it-practice.pdf»
Если все сделаете правильно, по ссылке выше будет открываться правильная страница в правильном PDFе.
Ну и наконец, вики-разметкой напишите ваше понимание, почему правильный ответ — правильный, а неправильные варианты — неправильны.
Тут тоже могут быть полезны ссылки на википедию, решение вами рекуррентных уравнений в sympy.
Задача зарезервирована: StasFomin 00:31, 25 декабря 2024 (UTC)
Задача «2019-gate-computer-science-and-it-practice.pdf/Q12-alg2»
Вопрос: Q12-alg2-31d68c
Вопрос из «Algorithms Test 2» где-то со страницы 226.
Тут вставьте перевод вопроса.
Используйте возможности разметки, включая формулы и т.п, если будут графы — посмотрите как задать их текстом https://wiki.4intra.net/Graphviz (реально оценю, полезный навык). Если код — теги «code-pascal», «code-c» или «code-python» (не «source lang»).
В IT вообще не принято писать романы, всегда старайтесь писать структурированные (списками-абзацами тексты). Списки в MediaWiki — это просто «*». Не забывайте о них.
Преформатированный моноширинный текст — просто отступ.
Старайтесь нетривиальные понятия, особенно незнакомые вам, найти ссылку на википедию и вставить (нейросети лажают!).
Это важно, чтобы найти корректный перевод (то, что в википедии, или на худой конец — точно массово гуглится).
Потом конечно сотрите эти инструкции, которые тут курсивом или в блоке цитирования.
Ответы
Если ответы простые, однострочные, используйте простой способ задания ответов списком, типа так (префикс «Правильный ответ:» — это дословно, для правильного ответа, неважно, какой он будет в списке)
- Правильный ответ: тут реально правильный ответ
- неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
Если ответы длинные, многострочные, или там графы, используйте способ задания ответов разделами, Но такое очень редко встречается, например 2011-gre-cs-practice-book.pdf/Q05.
Объяснение
Сначала заполните номер страницы с этим вопросом Исходники — вопрос 12 на тут-номер-страницы-с-вопросом-12 странице книги «2019-gate-computer-science-and-it-practice.pdf»
Если все сделаете правильно, по ссылке выше будет открываться правильная страница в правильном PDFе.
Ну и наконец, вики-разметкой напишите ваше понимание, почему правильный ответ — правильный, а неправильные варианты — неправильны.
Тут тоже могут быть полезны ссылки на википедию, решение вами рекуррентных уравнений в sympy.
Задача зарезервирована: StasFomin 00:31, 25 декабря 2024 (UTC)
Задача «2019-gate-computer-science-and-it-practice.pdf/Q08-alg2»
Вопрос: Q08-alg2-31d68c
Вопрос из «Algorithms Test 2» где-то со страницы 226.
Тут вставьте перевод вопроса.
Используйте возможности разметки, включая формулы и т.п, если будут графы — посмотрите как задать их текстом https://wiki.4intra.net/Graphviz (реально оценю, полезный навык). Если код — теги «code-pascal», «code-c» или «code-python» (не «source lang»).
В IT вообще не принято писать романы, всегда старайтесь писать структурированные (списками-абзацами тексты). Списки в MediaWiki — это просто «*». Не забывайте о них.
Преформатированный моноширинный текст — просто отступ.
Старайтесь нетривиальные понятия, особенно незнакомые вам, найти ссылку на википедию и вставить (нейросети лажают!).
Это важно, чтобы найти корректный перевод (то, что в википедии, или на худой конец — точно массово гуглится).
Потом конечно сотрите эти инструкции, которые тут курсивом или в блоке цитирования.
Ответы
Если ответы простые, однострочные, используйте простой способ задания ответов списком, типа так (префикс «Правильный ответ:» — это дословно, для правильного ответа, неважно, какой он будет в списке)
- Правильный ответ: тут реально правильный ответ
- неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
Если ответы длинные, многострочные, или там графы, используйте способ задания ответов разделами, Но такое очень редко встречается, например 2011-gre-cs-practice-book.pdf/Q05.
Объяснение
Сначала заполните номер страницы с этим вопросом Исходники — вопрос 8 на тут-номер-страницы-с-вопросом-8 странице книги «2019-gate-computer-science-and-it-practice.pdf»
Если все сделаете правильно, по ссылке выше будет открываться правильная страница в правильном PDFе.
Ну и наконец, вики-разметкой напишите ваше понимание, почему правильный ответ — правильный, а неправильные варианты — неправильны.
Тут тоже могут быть полезны ссылки на википедию, решение вами рекуррентных уравнений в sympy.
Задача зарезервирована: StasFomin 00:30, 25 декабря 2024 (UTC)
Задача «2019-gate-computer-science-and-it-practice.pdf/Q09-alg2»
Вопрос: Q09-alg2-31d68c
Вопрос из «Algorithms Test 2» где-то со страницы 226.
Тут вставьте перевод вопроса.
Используйте возможности разметки, включая формулы и т.п, если будут графы — посмотрите как задать их текстом https://wiki.4intra.net/Graphviz (реально оценю, полезный навык). Если код — теги «code-pascal», «code-c» или «code-python» (не «source lang»).
В IT вообще не принято писать романы, всегда старайтесь писать структурированные (списками-абзацами тексты). Списки в MediaWiki — это просто «*». Не забывайте о них.
Преформатированный моноширинный текст — просто отступ.
Старайтесь нетривиальные понятия, особенно незнакомые вам, найти ссылку на википедию и вставить (нейросети лажают!).
Это важно, чтобы найти корректный перевод (то, что в википедии, или на худой конец — точно массово гуглится).
Потом конечно сотрите эти инструкции, которые тут курсивом или в блоке цитирования.
Ответы
Если ответы простые, однострочные, используйте простой способ задания ответов списком, типа так (префикс «Правильный ответ:» — это дословно, для правильного ответа, неважно, какой он будет в списке)
- Правильный ответ: тут реально правильный ответ
- неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
Если ответы длинные, многострочные, или там графы, используйте способ задания ответов разделами, Но такое очень редко встречается, например 2011-gre-cs-practice-book.pdf/Q05.
Объяснение
Сначала заполните номер страницы с этим вопросом Исходники — вопрос 9 на тут-номер-страницы-с-вопросом-9 странице книги «2019-gate-computer-science-and-it-practice.pdf»
Если все сделаете правильно, по ссылке выше будет открываться правильная страница в правильном PDFе.
Ну и наконец, вики-разметкой напишите ваше понимание, почему правильный ответ — правильный, а неправильные варианты — неправильны.
Тут тоже могут быть полезны ссылки на википедию, решение вами рекуррентных уравнений в sympy.
Задача зарезервирована: StasFomin 00:30, 25 декабря 2024 (UTC)
Задача «2019-gate-computer-science-and-it-practice.pdf/Q06-alg2»
Вопрос: Q06-alg2-31d68c
Вопрос из «Algorithms Test 2» где-то со страницы 226.
Тут вставьте перевод вопроса.
Используйте возможности разметки, включая формулы и т.п, если будут графы — посмотрите как задать их текстом https://wiki.4intra.net/Graphviz (реально оценю, полезный навык). Если код — теги «code-pascal», «code-c» или «code-python» (не «source lang»).
В IT вообще не принято писать романы, всегда старайтесь писать структурированные (списками-абзацами тексты). Списки в MediaWiki — это просто «*». Не забывайте о них.
Преформатированный моноширинный текст — просто отступ.
Старайтесь нетривиальные понятия, особенно незнакомые вам, найти ссылку на википедию и вставить (нейросети лажают!).
Это важно, чтобы найти корректный перевод (то, что в википедии, или на худой конец — точно массово гуглится).
Потом конечно сотрите эти инструкции, которые тут курсивом или в блоке цитирования.
Ответы
Если ответы простые, однострочные, используйте простой способ задания ответов списком, типа так (префикс «Правильный ответ:» — это дословно, для правильного ответа, неважно, какой он будет в списке)
- Правильный ответ: тут реально правильный ответ
- неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
Если ответы длинные, многострочные, или там графы, используйте способ задания ответов разделами, Но такое очень редко встречается, например 2011-gre-cs-practice-book.pdf/Q05.
Объяснение
Сначала заполните номер страницы с этим вопросом Исходники — вопрос 6 на тут-номер-страницы-с-вопросом-6 странице книги «2019-gate-computer-science-and-it-practice.pdf»
Если все сделаете правильно, по ссылке выше будет открываться правильная страница в правильном PDFе.
Ну и наконец, вики-разметкой напишите ваше понимание, почему правильный ответ — правильный, а неправильные варианты — неправильны.
Тут тоже могут быть полезны ссылки на википедию, решение вами рекуррентных уравнений в sympy.
Задача зарезервирована: StasFomin 00:30, 25 декабря 2024 (UTC)
Задача «2019-gate-computer-science-and-it-practice.pdf/Q02-alg2»
Вопрос: Q02-alg2-31d68c
Вопрос из «Algorithms Test 2» где-то со страницы 226.
Тут вставьте перевод вопроса.
Используйте возможности разметки, включая формулы и т.п, если будут графы — посмотрите как задать их текстом https://wiki.4intra.net/Graphviz (реально оценю, полезный навык). Если код — теги «code-pascal», «code-c» или «code-python» (не «source lang»).
В IT вообще не принято писать романы, всегда старайтесь писать структурированные (списками-абзацами тексты). Списки в MediaWiki — это просто «*». Не забывайте о них.
Преформатированный моноширинный текст — просто отступ.
Старайтесь нетривиальные понятия, особенно незнакомые вам, найти ссылку на википедию и вставить (нейросети лажают!).
Это важно, чтобы найти корректный перевод (то, что в википедии, или на худой конец — точно массово гуглится).
Потом конечно сотрите эти инструкции, которые тут курсивом или в блоке цитирования.
Ответы
Если ответы простые, однострочные, используйте простой способ задания ответов списком, типа так (префикс «Правильный ответ:» — это дословно, для правильного ответа, неважно, какой он будет в списке)
- Правильный ответ: тут реально правильный ответ
- неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
Если ответы длинные, многострочные, или там графы, используйте способ задания ответов разделами, Но такое очень редко встречается, например 2011-gre-cs-practice-book.pdf/Q05.
Объяснение
Сначала заполните номер страницы с этим вопросом Исходники — вопрос 2 на тут-номер-страницы-с-вопросом-2 странице книги «2019-gate-computer-science-and-it-practice.pdf»
Если все сделаете правильно, по ссылке выше будет открываться правильная страница в правильном PDFе.
Ну и наконец, вики-разметкой напишите ваше понимание, почему правильный ответ — правильный, а неправильные варианты — неправильны.
Тут тоже могут быть полезны ссылки на википедию, решение вами рекуррентных уравнений в sympy.
Задача зарезервирована: StasFomin 00:30, 25 декабря 2024 (UTC)
Задача «2019-gate-computer-science-and-it-practice.pdf/Q05-alg2»
Вопрос: Q05-alg2-31d68c
Вопрос из «Algorithms Test 2» где-то со страницы 226.
Тут вставьте перевод вопроса.
Используйте возможности разметки, включая формулы и т.п, если будут графы — посмотрите как задать их текстом https://wiki.4intra.net/Graphviz (реально оценю, полезный навык). Если код — теги «code-pascal», «code-c» или «code-python» (не «source lang»).
В IT вообще не принято писать романы, всегда старайтесь писать структурированные (списками-абзацами тексты). Списки в MediaWiki — это просто «*». Не забывайте о них.
Преформатированный моноширинный текст — просто отступ.
Старайтесь нетривиальные понятия, особенно незнакомые вам, найти ссылку на википедию и вставить (нейросети лажают!).
Это важно, чтобы найти корректный перевод (то, что в википедии, или на худой конец — точно массово гуглится).
Потом конечно сотрите эти инструкции, которые тут курсивом или в блоке цитирования.
Ответы
Если ответы простые, однострочные, используйте простой способ задания ответов списком, типа так (префикс «Правильный ответ:» — это дословно, для правильного ответа, неважно, какой он будет в списке)
- Правильный ответ: тут реально правильный ответ
- неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
Если ответы длинные, многострочные, или там графы, используйте способ задания ответов разделами, Но такое очень редко встречается, например 2011-gre-cs-practice-book.pdf/Q05.
Объяснение
Сначала заполните номер страницы с этим вопросом Исходники — вопрос 5 на тут-номер-страницы-с-вопросом-5 странице книги «2019-gate-computer-science-and-it-practice.pdf»
Если все сделаете правильно, по ссылке выше будет открываться правильная страница в правильном PDFе.
Ну и наконец, вики-разметкой напишите ваше понимание, почему правильный ответ — правильный, а неправильные варианты — неправильны.
Тут тоже могут быть полезны ссылки на википедию, решение вами рекуррентных уравнений в sympy.
Задача зарезервирована: StasFomin 00:30, 25 декабря 2024 (UTC)
Задача «2019-gate-computer-science-and-it-practice.pdf/Q01-alg2»
Вопрос: Q01-alg2-31d68c
Вопрос из «Algorithms Test 2» где-то со страницы 226.
Тут вставьте перевод вопроса.
Используйте возможности разметки, включая формулы и т.п, если будут графы — посмотрите как задать их текстом https://wiki.4intra.net/Graphviz (реально оценю, полезный навык). Если код — теги «code-pascal», «code-c» или «code-python» (не «source lang»).
В IT вообще не принято писать романы, всегда старайтесь писать структурированные (списками-абзацами тексты). Списки в MediaWiki — это просто «*». Не забывайте о них.
Преформатированный моноширинный текст — просто отступ.
Старайтесь нетривиальные понятия, особенно незнакомые вам, найти ссылку на википедию и вставить (нейросети лажают!).
Это важно, чтобы найти корректный перевод (то, что в википедии, или на худой конец — точно массово гуглится).
Потом конечно сотрите эти инструкции, которые тут курсивом или в блоке цитирования.
Ответы
Если ответы простые, однострочные, используйте простой способ задания ответов списком, типа так (префикс «Правильный ответ:» — это дословно, для правильного ответа, неважно, какой он будет в списке)
- Правильный ответ: тут реально правильный ответ
- неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
Если ответы длинные, многострочные, или там графы, используйте способ задания ответов разделами, Но такое очень редко встречается, например 2011-gre-cs-practice-book.pdf/Q05.
Объяснение
Сначала заполните номер страницы с этим вопросом Исходники — вопрос 1 на тут-номер-страницы-с-вопросом-1 странице книги «2019-gate-computer-science-and-it-practice.pdf»
Если все сделаете правильно, по ссылке выше будет открываться правильная страница в правильном PDFе.
Ну и наконец, вики-разметкой напишите ваше понимание, почему правильный ответ — правильный, а неправильные варианты — неправильны.
Тут тоже могут быть полезны ссылки на википедию, решение вами рекуррентных уравнений в sympy.
Задача зарезервирована: StasFomin 00:30, 25 декабря 2024 (UTC)
Задача «2019-gate-computer-science-and-it-practice.pdf/Q35-alg1»
Вопрос: Q35-alg1-31d68c
Вопрос из «Algorithms Test 1» где-то со страницы 222.
Тут вставьте перевод вопроса.
Используйте возможности разметки, включая формулы и т.п, если будут графы — посмотрите как задать их текстом https://wiki.4intra.net/Graphviz (реально оценю, полезный навык). Если код — теги «code-pascal», «code-c» или «code-python» (не «source lang»).
В IT вообще не принято писать романы, всегда старайтесь писать структурированные (списками-абзацами тексты). Списки в MediaWiki — это просто «*». Не забывайте о них.
Преформатированный моноширинный текст — просто отступ.
Старайтесь нетривиальные понятия, особенно незнакомые вам, найти ссылку на википедию и вставить (нейросети лажают!).
Это важно, чтобы найти корректный перевод (то, что в википедии, или на худой конец — точно массово гуглится).
Потом конечно сотрите эти инструкции, которые тут курсивом или в блоке цитирования.
Ответы
Если ответы простые, однострочные, используйте простой способ задания ответов списком, типа так (префикс «Правильный ответ:» — это дословно, для правильного ответа, неважно, какой он будет в списке)
- Правильный ответ: тут реально правильный ответ
- неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
Если ответы длинные, многострочные, или там графы, используйте способ задания ответов разделами, Но такое очень редко встречается, например 2011-gre-cs-practice-book.pdf/Q05.
Объяснение
Сначала заполните номер страницы с этим вопросом Исходники — вопрос 35 на тут-номер-страницы-с-вопросом-35 странице книги «2019-gate-computer-science-and-it-practice.pdf»
Если все сделаете правильно, по ссылке выше будет открываться правильная страница в правильном PDFе.
Ну и наконец, вики-разметкой напишите ваше понимание, почему правильный ответ — правильный, а неправильные варианты — неправильны.
Тут тоже могут быть полезны ссылки на википедию, решение вами рекуррентных уравнений в sympy.
Задача зарезервирована: StasFomin 20:48, 24 декабря 2024 (UTC)
Задача «2019-gate-computer-science-and-it-practice.pdf/Q33-alg1»
Вопрос: Q33-alg1-31d68c
Вопрос из «Algorithms Test 1» где-то со страницы 222.
Тут вставьте перевод вопроса.
Используйте возможности разметки, включая формулы и т.п, если будут графы — посмотрите как задать их текстом https://wiki.4intra.net/Graphviz (реально оценю, полезный навык). Если код — теги «code-pascal», «code-c» или «code-python» (не «source lang»).
В IT вообще не принято писать романы, всегда старайтесь писать структурированные (списками-абзацами тексты). Списки в MediaWiki — это просто «*». Не забывайте о них.
Преформатированный моноширинный текст — просто отступ.
Старайтесь нетривиальные понятия, особенно незнакомые вам, найти ссылку на википедию и вставить (нейросети лажают!).
Это важно, чтобы найти корректный перевод (то, что в википедии, или на худой конец — точно массово гуглится).
Потом конечно сотрите эти инструкции, которые тут курсивом или в блоке цитирования.
Ответы
Если ответы простые, однострочные, используйте простой способ задания ответов списком, типа так (префикс «Правильный ответ:» — это дословно, для правильного ответа, неважно, какой он будет в списке)
- Правильный ответ: тут реально правильный ответ
- неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
Если ответы длинные, многострочные, или там графы, используйте способ задания ответов разделами, Но такое очень редко встречается, например 2011-gre-cs-practice-book.pdf/Q05.
Объяснение
Сначала заполните номер страницы с этим вопросом Исходники — вопрос 33 на тут-номер-страницы-с-вопросом-33 странице книги «2019-gate-computer-science-and-it-practice.pdf»
Если все сделаете правильно, по ссылке выше будет открываться правильная страница в правильном PDFе.
Ну и наконец, вики-разметкой напишите ваше понимание, почему правильный ответ — правильный, а неправильные варианты — неправильны.
Тут тоже могут быть полезны ссылки на википедию, решение вами рекуррентных уравнений в sympy.
Задача зарезервирована: StasFomin 20:48, 24 декабря 2024 (UTC)
Задача «2019-gate-computer-science-and-it-practice.pdf/Q34-alg1»
Вопрос: Q34-alg1-31d68c
Вопрос из «Algorithms Test 1» где-то со страницы 222.
Тут вставьте перевод вопроса.
Используйте возможности разметки, включая формулы и т.п, если будут графы — посмотрите как задать их текстом https://wiki.4intra.net/Graphviz (реально оценю, полезный навык). Если код — теги «code-pascal», «code-c» или «code-python» (не «source lang»).
В IT вообще не принято писать романы, всегда старайтесь писать структурированные (списками-абзацами тексты). Списки в MediaWiki — это просто «*». Не забывайте о них.
Преформатированный моноширинный текст — просто отступ.
Старайтесь нетривиальные понятия, особенно незнакомые вам, найти ссылку на википедию и вставить (нейросети лажают!).
Это важно, чтобы найти корректный перевод (то, что в википедии, или на худой конец — точно массово гуглится).
Потом конечно сотрите эти инструкции, которые тут курсивом или в блоке цитирования.
Ответы
Если ответы простые, однострочные, используйте простой способ задания ответов списком, типа так (префикс «Правильный ответ:» — это дословно, для правильного ответа, неважно, какой он будет в списке)
- Правильный ответ: тут реально правильный ответ
- неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
Если ответы длинные, многострочные, или там графы, используйте способ задания ответов разделами, Но такое очень редко встречается, например 2011-gre-cs-practice-book.pdf/Q05.
Объяснение
Сначала заполните номер страницы с этим вопросом Исходники — вопрос 34 на тут-номер-страницы-с-вопросом-34 странице книги «2019-gate-computer-science-and-it-practice.pdf»
Если все сделаете правильно, по ссылке выше будет открываться правильная страница в правильном PDFе.
Ну и наконец, вики-разметкой напишите ваше понимание, почему правильный ответ — правильный, а неправильные варианты — неправильны.
Тут тоже могут быть полезны ссылки на википедию, решение вами рекуррентных уравнений в sympy.
Задача зарезервирована: StasFomin 20:48, 24 декабря 2024 (UTC)
Задача «2019-gate-computer-science-and-it-practice.pdf/Q30-alg1»
Вопрос: Q30-alg1-31d68c
Вопрос из «Algorithms Test 1» где-то со страницы 222.
Тут вставьте перевод вопроса.
Используйте возможности разметки, включая формулы и т.п, если будут графы — посмотрите как задать их текстом https://wiki.4intra.net/Graphviz (реально оценю, полезный навык). Если код — теги «code-pascal», «code-c» или «code-python» (не «source lang»).
В IT вообще не принято писать романы, всегда старайтесь писать структурированные (списками-абзацами тексты). Списки в MediaWiki — это просто «*». Не забывайте о них.
Преформатированный моноширинный текст — просто отступ.
Старайтесь нетривиальные понятия, особенно незнакомые вам, найти ссылку на википедию и вставить (нейросети лажают!).
Это важно, чтобы найти корректный перевод (то, что в википедии, или на худой конец — точно массово гуглится).
Потом конечно сотрите эти инструкции, которые тут курсивом или в блоке цитирования.
Ответы
Если ответы простые, однострочные, используйте простой способ задания ответов списком, типа так (префикс «Правильный ответ:» — это дословно, для правильного ответа, неважно, какой он будет в списке)
- Правильный ответ: тут реально правильный ответ
- неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
Если ответы длинные, многострочные, или там графы, используйте способ задания ответов разделами, Но такое очень редко встречается, например 2011-gre-cs-practice-book.pdf/Q05.
Объяснение
Сначала заполните номер страницы с этим вопросом Исходники — вопрос 30 на тут-номер-страницы-с-вопросом-30 странице книги «2019-gate-computer-science-and-it-practice.pdf»
Если все сделаете правильно, по ссылке выше будет открываться правильная страница в правильном PDFе.
Ну и наконец, вики-разметкой напишите ваше понимание, почему правильный ответ — правильный, а неправильные варианты — неправильны.
Тут тоже могут быть полезны ссылки на википедию, решение вами рекуррентных уравнений в sympy.
Задача зарезервирована: StasFomin 20:48, 24 декабря 2024 (UTC)
Задача «2019-gate-computer-science-and-it-practice.pdf/Q26-alg1»
Вопрос: Q26-alg1-31d68c
Вопрос из «Algorithms Test 1» где-то со страницы 222.
Тут вставьте перевод вопроса.
Используйте возможности разметки, включая формулы и т.п, если будут графы — посмотрите как задать их текстом https://wiki.4intra.net/Graphviz (реально оценю, полезный навык). Если код — теги «code-pascal», «code-c» или «code-python» (не «source lang»).
В IT вообще не принято писать романы, всегда старайтесь писать структурированные (списками-абзацами тексты). Списки в MediaWiki — это просто «*». Не забывайте о них.
Преформатированный моноширинный текст — просто отступ.
Старайтесь нетривиальные понятия, особенно незнакомые вам, найти ссылку на википедию и вставить (нейросети лажают!).
Это важно, чтобы найти корректный перевод (то, что в википедии, или на худой конец — точно массово гуглится).
Потом конечно сотрите эти инструкции, которые тут курсивом или в блоке цитирования.
Ответы
Если ответы простые, однострочные, используйте простой способ задания ответов списком, типа так (префикс «Правильный ответ:» — это дословно, для правильного ответа, неважно, какой он будет в списке)
- Правильный ответ: тут реально правильный ответ
- неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
Если ответы длинные, многострочные, или там графы, используйте способ задания ответов разделами, Но такое очень редко встречается, например 2011-gre-cs-practice-book.pdf/Q05.
Объяснение
Сначала заполните номер страницы с этим вопросом Исходники — вопрос 26 на тут-номер-страницы-с-вопросом-26 странице книги «2019-gate-computer-science-and-it-practice.pdf»
Если все сделаете правильно, по ссылке выше будет открываться правильная страница в правильном PDFе.
Ну и наконец, вики-разметкой напишите ваше понимание, почему правильный ответ — правильный, а неправильные варианты — неправильны.
Тут тоже могут быть полезны ссылки на википедию, решение вами рекуррентных уравнений в sympy.
Задача зарезервирована: StasFomin 20:48, 24 декабря 2024 (UTC)
Задача «2019-gate-computer-science-and-it-practice.pdf/Q27-alg1»
Вопрос: Q27-alg1-31d68c
Вопрос из «Algorithms Test 1» где-то со страницы 222.
Тут вставьте перевод вопроса.
Используйте возможности разметки, включая формулы и т.п, если будут графы — посмотрите как задать их текстом https://wiki.4intra.net/Graphviz (реально оценю, полезный навык). Если код — теги «code-pascal», «code-c» или «code-python» (не «source lang»).
В IT вообще не принято писать романы, всегда старайтесь писать структурированные (списками-абзацами тексты). Списки в MediaWiki — это просто «*». Не забывайте о них.
Преформатированный моноширинный текст — просто отступ.
Старайтесь нетривиальные понятия, особенно незнакомые вам, найти ссылку на википедию и вставить (нейросети лажают!).
Это важно, чтобы найти корректный перевод (то, что в википедии, или на худой конец — точно массово гуглится).
Потом конечно сотрите эти инструкции, которые тут курсивом или в блоке цитирования.
Ответы
Если ответы простые, однострочные, используйте простой способ задания ответов списком, типа так (префикс «Правильный ответ:» — это дословно, для правильного ответа, неважно, какой он будет в списке)
- Правильный ответ: тут реально правильный ответ
- неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
Если ответы длинные, многострочные, или там графы, используйте способ задания ответов разделами, Но такое очень редко встречается, например 2011-gre-cs-practice-book.pdf/Q05.
Объяснение
Сначала заполните номер страницы с этим вопросом Исходники — вопрос 27 на тут-номер-страницы-с-вопросом-27 странице книги «2019-gate-computer-science-and-it-practice.pdf»
Если все сделаете правильно, по ссылке выше будет открываться правильная страница в правильном PDFе.
Ну и наконец, вики-разметкой напишите ваше понимание, почему правильный ответ — правильный, а неправильные варианты — неправильны.
Тут тоже могут быть полезны ссылки на википедию, решение вами рекуррентных уравнений в sympy.
Задача зарезервирована: StasFomin 20:48, 24 декабря 2024 (UTC)
Задача «2019-gate-computer-science-and-it-practice.pdf/Q28-alg1»
Вопрос: Q28-alg1-31d68c
Вопрос из «Algorithms Test 1» где-то со страницы 222.
Тут вставьте перевод вопроса.
Используйте возможности разметки, включая формулы и т.п, если будут графы — посмотрите как задать их текстом https://wiki.4intra.net/Graphviz (реально оценю, полезный навык). Если код — теги «code-pascal», «code-c» или «code-python» (не «source lang»).
В IT вообще не принято писать романы, всегда старайтесь писать структурированные (списками-абзацами тексты). Списки в MediaWiki — это просто «*». Не забывайте о них.
Преформатированный моноширинный текст — просто отступ.
Старайтесь нетривиальные понятия, особенно незнакомые вам, найти ссылку на википедию и вставить (нейросети лажают!).
Это важно, чтобы найти корректный перевод (то, что в википедии, или на худой конец — точно массово гуглится).
Потом конечно сотрите эти инструкции, которые тут курсивом или в блоке цитирования.
Ответы
Если ответы простые, однострочные, используйте простой способ задания ответов списком, типа так (префикс «Правильный ответ:» — это дословно, для правильного ответа, неважно, какой он будет в списке)
- Правильный ответ: тут реально правильный ответ
- неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
Если ответы длинные, многострочные, или там графы, используйте способ задания ответов разделами, Но такое очень редко встречается, например 2011-gre-cs-practice-book.pdf/Q05.
Объяснение
Сначала заполните номер страницы с этим вопросом Исходники — вопрос 28 на тут-номер-страницы-с-вопросом-28 странице книги «2019-gate-computer-science-and-it-practice.pdf»
Если все сделаете правильно, по ссылке выше будет открываться правильная страница в правильном PDFе.
Ну и наконец, вики-разметкой напишите ваше понимание, почему правильный ответ — правильный, а неправильные варианты — неправильны.
Тут тоже могут быть полезны ссылки на википедию, решение вами рекуррентных уравнений в sympy.
Задача зарезервирована: StasFomin 20:48, 24 декабря 2024 (UTC)
Задача «2019-gate-computer-science-and-it-practice.pdf/Q24-alg1»
Вопрос: Q24-alg1-31d68c
Вопрос из «Algorithms Test 1» где-то со страницы 222.
Тут вставьте перевод вопроса.
Используйте возможности разметки, включая формулы и т.п, если будут графы — посмотрите как задать их текстом https://wiki.4intra.net/Graphviz (реально оценю, полезный навык). Если код — теги «code-pascal», «code-c» или «code-python» (не «source lang»).
В IT вообще не принято писать романы, всегда старайтесь писать структурированные (списками-абзацами тексты). Списки в MediaWiki — это просто «*». Не забывайте о них.
Преформатированный моноширинный текст — просто отступ.
Старайтесь нетривиальные понятия, особенно незнакомые вам, найти ссылку на википедию и вставить (нейросети лажают!).
Это важно, чтобы найти корректный перевод (то, что в википедии, или на худой конец — точно массово гуглится).
Потом конечно сотрите эти инструкции, которые тут курсивом или в блоке цитирования.
Ответы
Если ответы простые, однострочные, используйте простой способ задания ответов списком, типа так (префикс «Правильный ответ:» — это дословно, для правильного ответа, неважно, какой он будет в списке)
- Правильный ответ: тут реально правильный ответ
- неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
Если ответы длинные, многострочные, или там графы, используйте способ задания ответов разделами, Но такое очень редко встречается, например 2011-gre-cs-practice-book.pdf/Q05.
Объяснение
Сначала заполните номер страницы с этим вопросом Исходники — вопрос 24 на тут-номер-страницы-с-вопросом-24 странице книги «2019-gate-computer-science-and-it-practice.pdf»
Если все сделаете правильно, по ссылке выше будет открываться правильная страница в правильном PDFе.
Ну и наконец, вики-разметкой напишите ваше понимание, почему правильный ответ — правильный, а неправильные варианты — неправильны.
Тут тоже могут быть полезны ссылки на википедию, решение вами рекуррентных уравнений в sympy.
Задача зарезервирована: StasFomin 20:47, 24 декабря 2024 (UTC)
Задача «2019-gate-computer-science-and-it-practice.pdf/Q25-alg1»
Вопрос: Q25-alg1-31d68c
Вопрос из «Algorithms Test 1» где-то со страницы 222.
Тут вставьте перевод вопроса.
Используйте возможности разметки, включая формулы и т.п, если будут графы — посмотрите как задать их текстом https://wiki.4intra.net/Graphviz (реально оценю, полезный навык). Если код — теги «code-pascal», «code-c» или «code-python» (не «source lang»).
В IT вообще не принято писать романы, всегда старайтесь писать структурированные (списками-абзацами тексты). Списки в MediaWiki — это просто «*». Не забывайте о них.
Преформатированный моноширинный текст — просто отступ.
Старайтесь нетривиальные понятия, особенно незнакомые вам, найти ссылку на википедию и вставить (нейросети лажают!).
Это важно, чтобы найти корректный перевод (то, что в википедии, или на худой конец — точно массово гуглится).
Потом конечно сотрите эти инструкции, которые тут курсивом или в блоке цитирования.
Ответы
Если ответы простые, однострочные, используйте простой способ задания ответов списком, типа так (префикс «Правильный ответ:» — это дословно, для правильного ответа, неважно, какой он будет в списке)
- Правильный ответ: тут реально правильный ответ
- неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
Если ответы длинные, многострочные, или там графы, используйте способ задания ответов разделами, Но такое очень редко встречается, например 2011-gre-cs-practice-book.pdf/Q05.
Объяснение
Сначала заполните номер страницы с этим вопросом Исходники — вопрос 25 на тут-номер-страницы-с-вопросом-25 странице книги «2019-gate-computer-science-and-it-practice.pdf»
Если все сделаете правильно, по ссылке выше будет открываться правильная страница в правильном PDFе.
Ну и наконец, вики-разметкой напишите ваше понимание, почему правильный ответ — правильный, а неправильные варианты — неправильны.
Тут тоже могут быть полезны ссылки на википедию, решение вами рекуррентных уравнений в sympy.
Задача зарезервирована: StasFomin 20:48, 24 декабря 2024 (UTC)
Задача «2019-gate-computer-science-and-it-practice.pdf/Q22-alg1»
Вопрос: Q22-alg1-31d68c
Вопрос из «Algorithms Test 1» где-то со страницы 222.
Тут вставьте перевод вопроса.
Используйте возможности разметки, включая формулы и т.п, если будут графы — посмотрите как задать их текстом https://wiki.4intra.net/Graphviz (реально оценю, полезный навык). Если код — теги «code-pascal», «code-c» или «code-python» (не «source lang»).
В IT вообще не принято писать романы, всегда старайтесь писать структурированные (списками-абзацами тексты). Списки в MediaWiki — это просто «*». Не забывайте о них.
Преформатированный моноширинный текст — просто отступ.
Старайтесь нетривиальные понятия, особенно незнакомые вам, найти ссылку на википедию и вставить (нейросети лажают!).
Это важно, чтобы найти корректный перевод (то, что в википедии, или на худой конец — точно массово гуглится).
Потом конечно сотрите эти инструкции, которые тут курсивом или в блоке цитирования.
Ответы
Если ответы простые, однострочные, используйте простой способ задания ответов списком, типа так (префикс «Правильный ответ:» — это дословно, для правильного ответа, неважно, какой он будет в списке)
- Правильный ответ: тут реально правильный ответ
- неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
Если ответы длинные, многострочные, или там графы, используйте способ задания ответов разделами, Но такое очень редко встречается, например 2011-gre-cs-practice-book.pdf/Q05.
Объяснение
Сначала заполните номер страницы с этим вопросом Исходники — вопрос 22 на тут-номер-страницы-с-вопросом-22 странице книги «2019-gate-computer-science-and-it-practice.pdf»
Если все сделаете правильно, по ссылке выше будет открываться правильная страница в правильном PDFе.
Ну и наконец, вики-разметкой напишите ваше понимание, почему правильный ответ — правильный, а неправильные варианты — неправильны.
Тут тоже могут быть полезны ссылки на википедию, решение вами рекуррентных уравнений в sympy.
Задача зарезервирована: StasFomin 20:47, 24 декабря 2024 (UTC)
Задача «2019-gate-computer-science-and-it-practice.pdf/Q23-alg1»
Вопрос: Q23-alg1-31d68c
Вопрос из «Algorithms Test 1» где-то со страницы 222.
Тут вставьте перевод вопроса.
Используйте возможности разметки, включая формулы и т.п, если будут графы — посмотрите как задать их текстом https://wiki.4intra.net/Graphviz (реально оценю, полезный навык). Если код — теги «code-pascal», «code-c» или «code-python» (не «source lang»).
В IT вообще не принято писать романы, всегда старайтесь писать структурированные (списками-абзацами тексты). Списки в MediaWiki — это просто «*». Не забывайте о них.
Преформатированный моноширинный текст — просто отступ.
Старайтесь нетривиальные понятия, особенно незнакомые вам, найти ссылку на википедию и вставить (нейросети лажают!).
Это важно, чтобы найти корректный перевод (то, что в википедии, или на худой конец — точно массово гуглится).
Потом конечно сотрите эти инструкции, которые тут курсивом или в блоке цитирования.
Ответы
Если ответы простые, однострочные, используйте простой способ задания ответов списком, типа так (префикс «Правильный ответ:» — это дословно, для правильного ответа, неважно, какой он будет в списке)
- Правильный ответ: тут реально правильный ответ
- неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
Если ответы длинные, многострочные, или там графы, используйте способ задания ответов разделами, Но такое очень редко встречается, например 2011-gre-cs-practice-book.pdf/Q05.
Объяснение
Сначала заполните номер страницы с этим вопросом Исходники — вопрос 23 на тут-номер-страницы-с-вопросом-23 странице книги «2019-gate-computer-science-and-it-practice.pdf»
Если все сделаете правильно, по ссылке выше будет открываться правильная страница в правильном PDFе.
Ну и наконец, вики-разметкой напишите ваше понимание, почему правильный ответ — правильный, а неправильные варианты — неправильны.
Тут тоже могут быть полезны ссылки на википедию, решение вами рекуррентных уравнений в sympy.
Задача зарезервирована: StasFomin 20:47, 24 декабря 2024 (UTC)
Задача «2019-gate-computer-science-and-it-practice.pdf/Q18-alg1»
Вопрос: Q18-alg1-31d68c
Вопрос из «Algorithms Test 1» где-то со страницы 222.
Тут вставьте перевод вопроса.
Используйте возможности разметки, включая формулы и т.п, если будут графы — посмотрите как задать их текстом https://wiki.4intra.net/Graphviz (реально оценю, полезный навык). Если код — теги «code-pascal», «code-c» или «code-python» (не «source lang»).
В IT вообще не принято писать романы, всегда старайтесь писать структурированные (списками-абзацами тексты). Списки в MediaWiki — это просто «*». Не забывайте о них.
Преформатированный моноширинный текст — просто отступ.
Старайтесь нетривиальные понятия, особенно незнакомые вам, найти ссылку на википедию и вставить (нейросети лажают!).
Это важно, чтобы найти корректный перевод (то, что в википедии, или на худой конец — точно массово гуглится).
Потом конечно сотрите эти инструкции, которые тут курсивом или в блоке цитирования.
Ответы
Если ответы простые, однострочные, используйте простой способ задания ответов списком, типа так (префикс «Правильный ответ:» — это дословно, для правильного ответа, неважно, какой он будет в списке)
- Правильный ответ: тут реально правильный ответ
- неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
Если ответы длинные, многострочные, или там графы, используйте способ задания ответов разделами, Но такое очень редко встречается, например 2011-gre-cs-practice-book.pdf/Q05.
Объяснение
Сначала заполните номер страницы с этим вопросом Исходники — вопрос 18 на тут-номер-страницы-с-вопросом-18 странице книги «2019-gate-computer-science-and-it-practice.pdf»
Если все сделаете правильно, по ссылке выше будет открываться правильная страница в правильном PDFе.
Ну и наконец, вики-разметкой напишите ваше понимание, почему правильный ответ — правильный, а неправильные варианты — неправильны.
Тут тоже могут быть полезны ссылки на википедию, решение вами рекуррентных уравнений в sympy.
Задача зарезервирована: StasFomin 20:47, 24 декабря 2024 (UTC)
Задача «2019-gate-computer-science-and-it-practice.pdf/Q19-alg1»
Вопрос: Q19-alg1-31d68c
Вопрос из «Algorithms Test 1» где-то со страницы 222.
Тут вставьте перевод вопроса.
Используйте возможности разметки, включая формулы и т.п, если будут графы — посмотрите как задать их текстом https://wiki.4intra.net/Graphviz (реально оценю, полезный навык). Если код — теги «code-pascal», «code-c» или «code-python» (не «source lang»).
В IT вообще не принято писать романы, всегда старайтесь писать структурированные (списками-абзацами тексты). Списки в MediaWiki — это просто «*». Не забывайте о них.
Преформатированный моноширинный текст — просто отступ.
Старайтесь нетривиальные понятия, особенно незнакомые вам, найти ссылку на википедию и вставить (нейросети лажают!).
Это важно, чтобы найти корректный перевод (то, что в википедии, или на худой конец — точно массово гуглится).
Потом конечно сотрите эти инструкции, которые тут курсивом или в блоке цитирования.
Ответы
Если ответы простые, однострочные, используйте простой способ задания ответов списком, типа так (префикс «Правильный ответ:» — это дословно, для правильного ответа, неважно, какой он будет в списке)
- Правильный ответ: тут реально правильный ответ
- неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
Если ответы длинные, многострочные, или там графы, используйте способ задания ответов разделами, Но такое очень редко встречается, например 2011-gre-cs-practice-book.pdf/Q05.
Объяснение
Сначала заполните номер страницы с этим вопросом Исходники — вопрос 19 на тут-номер-страницы-с-вопросом-19 странице книги «2019-gate-computer-science-and-it-practice.pdf»
Если все сделаете правильно, по ссылке выше будет открываться правильная страница в правильном PDFе.
Ну и наконец, вики-разметкой напишите ваше понимание, почему правильный ответ — правильный, а неправильные варианты — неправильны.
Тут тоже могут быть полезны ссылки на википедию, решение вами рекуррентных уравнений в sympy.
Задача зарезервирована: StasFomin 20:47, 24 декабря 2024 (UTC)
Задача «2019-gate-computer-science-and-it-practice.pdf/Q20-alg1»
Вопрос: Q20-alg1-31d68c
Вопрос из «Algorithms Test 1» где-то со страницы 222.
Тут вставьте перевод вопроса.
Используйте возможности разметки, включая формулы и т.п, если будут графы — посмотрите как задать их текстом https://wiki.4intra.net/Graphviz (реально оценю, полезный навык). Если код — теги «code-pascal», «code-c» или «code-python» (не «source lang»).
В IT вообще не принято писать романы, всегда старайтесь писать структурированные (списками-абзацами тексты). Списки в MediaWiki — это просто «*». Не забывайте о них.
Преформатированный моноширинный текст — просто отступ.
Старайтесь нетривиальные понятия, особенно незнакомые вам, найти ссылку на википедию и вставить (нейросети лажают!).
Это важно, чтобы найти корректный перевод (то, что в википедии, или на худой конец — точно массово гуглится).
Потом конечно сотрите эти инструкции, которые тут курсивом или в блоке цитирования.
Ответы
Если ответы простые, однострочные, используйте простой способ задания ответов списком, типа так (префикс «Правильный ответ:» — это дословно, для правильного ответа, неважно, какой он будет в списке)
- Правильный ответ: тут реально правильный ответ
- неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
Если ответы длинные, многострочные, или там графы, используйте способ задания ответов разделами, Но такое очень редко встречается, например 2011-gre-cs-practice-book.pdf/Q05.
Объяснение
Сначала заполните номер страницы с этим вопросом Исходники — вопрос 20 на тут-номер-страницы-с-вопросом-20 странице книги «2019-gate-computer-science-and-it-practice.pdf»
Если все сделаете правильно, по ссылке выше будет открываться правильная страница в правильном PDFе.
Ну и наконец, вики-разметкой напишите ваше понимание, почему правильный ответ — правильный, а неправильные варианты — неправильны.
Тут тоже могут быть полезны ссылки на википедию, решение вами рекуррентных уравнений в sympy.
Задача зарезервирована: StasFomin 20:47, 24 декабря 2024 (UTC)
Задача «2019-gate-computer-science-and-it-practice.pdf/Q16-alg1»
Вопрос: Q16-alg1-31d68c
Вопрос из «Algorithms Test 1» где-то со страницы 222.
Тут вставьте перевод вопроса.
Используйте возможности разметки, включая формулы и т.п, если будут графы — посмотрите как задать их текстом https://wiki.4intra.net/Graphviz (реально оценю, полезный навык). Если код — теги «code-pascal», «code-c» или «code-python» (не «source lang»).
В IT вообще не принято писать романы, всегда старайтесь писать структурированные (списками-абзацами тексты). Списки в MediaWiki — это просто «*». Не забывайте о них.
Преформатированный моноширинный текст — просто отступ.
Старайтесь нетривиальные понятия, особенно незнакомые вам, найти ссылку на википедию и вставить (нейросети лажают!).
Это важно, чтобы найти корректный перевод (то, что в википедии, или на худой конец — точно массово гуглится).
Потом конечно сотрите эти инструкции, которые тут курсивом или в блоке цитирования.
Ответы
Если ответы простые, однострочные, используйте простой способ задания ответов списком, типа так (префикс «Правильный ответ:» — это дословно, для правильного ответа, неважно, какой он будет в списке)
- Правильный ответ: тут реально правильный ответ
- неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
Если ответы длинные, многострочные, или там графы, используйте способ задания ответов разделами, Но такое очень редко встречается, например 2011-gre-cs-practice-book.pdf/Q05.
Объяснение
Сначала заполните номер страницы с этим вопросом Исходники — вопрос 16 на тут-номер-страницы-с-вопросом-16 странице книги «2019-gate-computer-science-and-it-practice.pdf»
Если все сделаете правильно, по ссылке выше будет открываться правильная страница в правильном PDFе.
Ну и наконец, вики-разметкой напишите ваше понимание, почему правильный ответ — правильный, а неправильные варианты — неправильны.
Тут тоже могут быть полезны ссылки на википедию, решение вами рекуррентных уравнений в sympy.
Задача зарезервирована: StasFomin 20:47, 24 декабря 2024 (UTC)
Задача «2019-gate-computer-science-and-it-practice.pdf/Q13-alg1»
Вопрос: Q13-alg1-31d68c
Вопрос из «Algorithms Test 1» где-то со страницы 222.
Тут вставьте перевод вопроса.
Используйте возможности разметки, включая формулы и т.п, если будут графы — посмотрите как задать их текстом https://wiki.4intra.net/Graphviz (реально оценю, полезный навык). Если код — теги «code-pascal», «code-c» или «code-python» (не «source lang»).
В IT вообще не принято писать романы, всегда старайтесь писать структурированные (списками-абзацами тексты). Списки в MediaWiki — это просто «*». Не забывайте о них.
Преформатированный моноширинный текст — просто отступ.
Старайтесь нетривиальные понятия, особенно незнакомые вам, найти ссылку на википедию и вставить (нейросети лажают!).
Это важно, чтобы найти корректный перевод (то, что в википедии, или на худой конец — точно массово гуглится).
Потом конечно сотрите эти инструкции, которые тут курсивом или в блоке цитирования.
Ответы
Если ответы простые, однострочные, используйте простой способ задания ответов списком, типа так (префикс «Правильный ответ:» — это дословно, для правильного ответа, неважно, какой он будет в списке)
- Правильный ответ: тут реально правильный ответ
- неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
Если ответы длинные, многострочные, или там графы, используйте способ задания ответов разделами, Но такое очень редко встречается, например 2011-gre-cs-practice-book.pdf/Q05.
Объяснение
Сначала заполните номер страницы с этим вопросом Исходники — вопрос 13 на тут-номер-страницы-с-вопросом-13 странице книги «2019-gate-computer-science-and-it-practice.pdf»
Если все сделаете правильно, по ссылке выше будет открываться правильная страница в правильном PDFе.
Ну и наконец, вики-разметкой напишите ваше понимание, почему правильный ответ — правильный, а неправильные варианты — неправильны.
Тут тоже могут быть полезны ссылки на википедию, решение вами рекуррентных уравнений в sympy.
Задача зарезервирована: StasFomin 20:47, 24 декабря 2024 (UTC)
Задача «2019-gate-computer-science-and-it-practice.pdf/Q08-alg1»
Вопрос: Q08-alg1-31d68c
Вопрос из «Algorithms Test 1» где-то со страницы 222.
Тут вставьте перевод вопроса.
Используйте возможности разметки, включая формулы и т.п, если будут графы — посмотрите как задать их текстом https://wiki.4intra.net/Graphviz (реально оценю, полезный навык). Если код — теги «code-pascal», «code-c» или «code-python» (не «source lang»).
В IT вообще не принято писать романы, всегда старайтесь писать структурированные (списками-абзацами тексты). Списки в MediaWiki — это просто «*». Не забывайте о них.
Преформатированный моноширинный текст — просто отступ.
Старайтесь нетривиальные понятия, особенно незнакомые вам, найти ссылку на википедию и вставить (нейросети лажают!).
Это важно, чтобы найти корректный перевод (то, что в википедии, или на худой конец — точно массово гуглится).
Потом конечно сотрите эти инструкции, которые тут курсивом или в блоке цитирования.
Ответы
Если ответы простые, однострочные, используйте простой способ задания ответов списком, типа так (префикс «Правильный ответ:» — это дословно, для правильного ответа, неважно, какой он будет в списке)
- Правильный ответ: тут реально правильный ответ
- неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
Если ответы длинные, многострочные, или там графы, используйте способ задания ответов разделами, Но такое очень редко встречается, например 2011-gre-cs-practice-book.pdf/Q05.
Объяснение
Сначала заполните номер страницы с этим вопросом Исходники — вопрос 8 на тут-номер-страницы-с-вопросом-8 странице книги «2019-gate-computer-science-and-it-practice.pdf»
Если все сделаете правильно, по ссылке выше будет открываться правильная страница в правильном PDFе.
Ну и наконец, вики-разметкой напишите ваше понимание, почему правильный ответ — правильный, а неправильные варианты — неправильны.
Тут тоже могут быть полезны ссылки на википедию, решение вами рекуррентных уравнений в sympy.
Задача зарезервирована: StasFomin 20:47, 24 декабря 2024 (UTC)
Задача «2019-gate-computer-science-and-it-practice.pdf/Q09-alg1»
Вопрос: Q09-alg1-31d68c
Вопрос из «Algorithms Test 1» где-то со страницы 222.
Тут вставьте перевод вопроса.
Используйте возможности разметки, включая формулы и т.п, если будут графы — посмотрите как задать их текстом https://wiki.4intra.net/Graphviz (реально оценю, полезный навык). Если код — теги «code-pascal», «code-c» или «code-python» (не «source lang»).
В IT вообще не принято писать романы, всегда старайтесь писать структурированные (списками-абзацами тексты). Списки в MediaWiki — это просто «*». Не забывайте о них.
Преформатированный моноширинный текст — просто отступ.
Старайтесь нетривиальные понятия, особенно незнакомые вам, найти ссылку на википедию и вставить (нейросети лажают!).
Это важно, чтобы найти корректный перевод (то, что в википедии, или на худой конец — точно массово гуглится).
Потом конечно сотрите эти инструкции, которые тут курсивом или в блоке цитирования.
Ответы
Если ответы простые, однострочные, используйте простой способ задания ответов списком, типа так (префикс «Правильный ответ:» — это дословно, для правильного ответа, неважно, какой он будет в списке)
- Правильный ответ: тут реально правильный ответ
- неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
Если ответы длинные, многострочные, или там графы, используйте способ задания ответов разделами, Но такое очень редко встречается, например 2011-gre-cs-practice-book.pdf/Q05.
Объяснение
Сначала заполните номер страницы с этим вопросом Исходники — вопрос 9 на тут-номер-страницы-с-вопросом-9 странице книги «2019-gate-computer-science-and-it-practice.pdf»
Если все сделаете правильно, по ссылке выше будет открываться правильная страница в правильном PDFе.
Ну и наконец, вики-разметкой напишите ваше понимание, почему правильный ответ — правильный, а неправильные варианты — неправильны.
Тут тоже могут быть полезны ссылки на википедию, решение вами рекуррентных уравнений в sympy.
Задача зарезервирована: StasFomin 20:47, 24 декабря 2024 (UTC)
Задача «2019-gate-computer-science-and-it-practice.pdf/Q10-alg1»
Вопрос: Q10-alg1-31d68c
Вопрос из «Algorithms Test 1» где-то со страницы 222.
Тут вставьте перевод вопроса.
Используйте возможности разметки, включая формулы и т.п, если будут графы — посмотрите как задать их текстом https://wiki.4intra.net/Graphviz (реально оценю, полезный навык). Если код — теги «code-pascal», «code-c» или «code-python» (не «source lang»).
В IT вообще не принято писать романы, всегда старайтесь писать структурированные (списками-абзацами тексты). Списки в MediaWiki — это просто «*». Не забывайте о них.
Преформатированный моноширинный текст — просто отступ.
Старайтесь нетривиальные понятия, особенно незнакомые вам, найти ссылку на википедию и вставить (нейросети лажают!).
Это важно, чтобы найти корректный перевод (то, что в википедии, или на худой конец — точно массово гуглится).
Потом конечно сотрите эти инструкции, которые тут курсивом или в блоке цитирования.
Ответы
Если ответы простые, однострочные, используйте простой способ задания ответов списком, типа так (префикс «Правильный ответ:» — это дословно, для правильного ответа, неважно, какой он будет в списке)
- Правильный ответ: тут реально правильный ответ
- неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
Если ответы длинные, многострочные, или там графы, используйте способ задания ответов разделами, Но такое очень редко встречается, например 2011-gre-cs-practice-book.pdf/Q05.
Объяснение
Сначала заполните номер страницы с этим вопросом Исходники — вопрос 10 на тут-номер-страницы-с-вопросом-10 странице книги «2019-gate-computer-science-and-it-practice.pdf»
Если все сделаете правильно, по ссылке выше будет открываться правильная страница в правильном PDFе.
Ну и наконец, вики-разметкой напишите ваше понимание, почему правильный ответ — правильный, а неправильные варианты — неправильны.
Тут тоже могут быть полезны ссылки на википедию, решение вами рекуррентных уравнений в sympy.
Задача зарезервирована: StasFomin 20:47, 24 декабря 2024 (UTC)
Задача «2019-gate-computer-science-and-it-practice.pdf/Q11-alg1»
Вопрос: Q11-alg1-31d68c
Вопрос из «Algorithms Test 1» где-то со страницы 222.
Тут вставьте перевод вопроса.
Используйте возможности разметки, включая формулы и т.п, если будут графы — посмотрите как задать их текстом https://wiki.4intra.net/Graphviz (реально оценю, полезный навык). Если код — теги «code-pascal», «code-c» или «code-python» (не «source lang»).
В IT вообще не принято писать романы, всегда старайтесь писать структурированные (списками-абзацами тексты). Списки в MediaWiki — это просто «*». Не забывайте о них.
Преформатированный моноширинный текст — просто отступ.
Старайтесь нетривиальные понятия, особенно незнакомые вам, найти ссылку на википедию и вставить (нейросети лажают!).
Это важно, чтобы найти корректный перевод (то, что в википедии, или на худой конец — точно массово гуглится).
Потом конечно сотрите эти инструкции, которые тут курсивом или в блоке цитирования.
Ответы
Если ответы простые, однострочные, используйте простой способ задания ответов списком, типа так (префикс «Правильный ответ:» — это дословно, для правильного ответа, неважно, какой он будет в списке)
- Правильный ответ: тут реально правильный ответ
- неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
Если ответы длинные, многострочные, или там графы, используйте способ задания ответов разделами, Но такое очень редко встречается, например 2011-gre-cs-practice-book.pdf/Q05.
Объяснение
Сначала заполните номер страницы с этим вопросом Исходники — вопрос 11 на тут-номер-страницы-с-вопросом-11 странице книги «2019-gate-computer-science-and-it-practice.pdf»
Если все сделаете правильно, по ссылке выше будет открываться правильная страница в правильном PDFе.
Ну и наконец, вики-разметкой напишите ваше понимание, почему правильный ответ — правильный, а неправильные варианты — неправильны.
Тут тоже могут быть полезны ссылки на википедию, решение вами рекуррентных уравнений в sympy.
Задача зарезервирована: StasFomin 20:47, 24 декабря 2024 (UTC)
Задача «2019-gate-computer-science-and-it-practice.pdf/Q12-alg1»
Вопрос: Q12-alg1-31d68c
Вопрос из «Algorithms Test 1» где-то со страницы 222.
Тут вставьте перевод вопроса.
Используйте возможности разметки, включая формулы и т.п, если будут графы — посмотрите как задать их текстом https://wiki.4intra.net/Graphviz (реально оценю, полезный навык). Если код — теги «code-pascal», «code-c» или «code-python» (не «source lang»).
В IT вообще не принято писать романы, всегда старайтесь писать структурированные (списками-абзацами тексты). Списки в MediaWiki — это просто «*». Не забывайте о них.
Преформатированный моноширинный текст — просто отступ.
Старайтесь нетривиальные понятия, особенно незнакомые вам, найти ссылку на википедию и вставить (нейросети лажают!).
Это важно, чтобы найти корректный перевод (то, что в википедии, или на худой конец — точно массово гуглится).
Потом конечно сотрите эти инструкции, которые тут курсивом или в блоке цитирования.
Ответы
Если ответы простые, однострочные, используйте простой способ задания ответов списком, типа так (префикс «Правильный ответ:» — это дословно, для правильного ответа, неважно, какой он будет в списке)
- Правильный ответ: тут реально правильный ответ
- неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
Если ответы длинные, многострочные, или там графы, используйте способ задания ответов разделами, Но такое очень редко встречается, например 2011-gre-cs-practice-book.pdf/Q05.
Объяснение
Сначала заполните номер страницы с этим вопросом Исходники — вопрос 12 на тут-номер-страницы-с-вопросом-12 странице книги «2019-gate-computer-science-and-it-practice.pdf»
Если все сделаете правильно, по ссылке выше будет открываться правильная страница в правильном PDFе.
Ну и наконец, вики-разметкой напишите ваше понимание, почему правильный ответ — правильный, а неправильные варианты — неправильны.
Тут тоже могут быть полезны ссылки на википедию, решение вами рекуррентных уравнений в sympy.
Задача зарезервирована: StasFomin 20:47, 24 декабря 2024 (UTC)
Задача «2019-gate-computer-science-and-it-practice.pdf/Q03-alg1»
Вопрос: Q03-alg1-31d68c
Вопрос из «Algorithms Test 1» где-то со страницы 222.
Тут вставьте перевод вопроса.
Используйте возможности разметки, включая формулы и т.п, если будут графы — посмотрите как задать их текстом https://wiki.4intra.net/Graphviz (реально оценю, полезный навык). Если код — теги «code-pascal», «code-c» или «code-python» (не «source lang»).
В IT вообще не принято писать романы, всегда старайтесь писать структурированные (списками-абзацами тексты). Списки в MediaWiki — это просто «*». Не забывайте о них.
Преформатированный моноширинный текст — просто отступ.
Старайтесь нетривиальные понятия, особенно незнакомые вам, найти ссылку на википедию и вставить (нейросети лажают!).
Это важно, чтобы найти корректный перевод (то, что в википедии, или на худой конец — точно массово гуглится).
Потом конечно сотрите эти инструкции, которые тут курсивом или в блоке цитирования.
Ответы
Если ответы простые, однострочные, используйте простой способ задания ответов списком, типа так (префикс «Правильный ответ:» — это дословно, для правильного ответа, неважно, какой он будет в списке)
- Правильный ответ: тут реально правильный ответ
- неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
Если ответы длинные, многострочные, или там графы, используйте способ задания ответов разделами, Но такое очень редко встречается, например 2011-gre-cs-practice-book.pdf/Q05.
Объяснение
Сначала заполните номер страницы с этим вопросом Исходники — вопрос 3 на тут-номер-страницы-с-вопросом-3 странице книги «2019-gate-computer-science-and-it-practice.pdf»
Если все сделаете правильно, по ссылке выше будет открываться правильная страница в правильном PDFе.
Ну и наконец, вики-разметкой напишите ваше понимание, почему правильный ответ — правильный, а неправильные варианты — неправильны.
Тут тоже могут быть полезны ссылки на википедию, решение вами рекуррентных уравнений в sympy.
Задача зарезервирована: StasFomin 20:47, 24 декабря 2024 (UTC)
Задача «2019-gate-computer-science-and-it-practice.pdf/Q04-alg1»
Вопрос: Q04-alg1-31d68c
Вопрос из «Algorithms Test 1» где-то со страницы 222.
Тут вставьте перевод вопроса.
Используйте возможности разметки, включая формулы и т.п, если будут графы — посмотрите как задать их текстом https://wiki.4intra.net/Graphviz (реально оценю, полезный навык). Если код — теги «code-pascal», «code-c» или «code-python» (не «source lang»).
В IT вообще не принято писать романы, всегда старайтесь писать структурированные (списками-абзацами тексты). Списки в MediaWiki — это просто «*». Не забывайте о них.
Преформатированный моноширинный текст — просто отступ.
Старайтесь нетривиальные понятия, особенно незнакомые вам, найти ссылку на википедию и вставить (нейросети лажают!).
Это важно, чтобы найти корректный перевод (то, что в википедии, или на худой конец — точно массово гуглится).
Потом конечно сотрите эти инструкции, которые тут курсивом или в блоке цитирования.
Ответы
Если ответы простые, однострочные, используйте простой способ задания ответов списком, типа так (префикс «Правильный ответ:» — это дословно, для правильного ответа, неважно, какой он будет в списке)
- Правильный ответ: тут реально правильный ответ
- неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
Если ответы длинные, многострочные, или там графы, используйте способ задания ответов разделами, Но такое очень редко встречается, например 2011-gre-cs-practice-book.pdf/Q05.
Объяснение
Сначала заполните номер страницы с этим вопросом Исходники — вопрос 4 на тут-номер-страницы-с-вопросом-4 странице книги «2019-gate-computer-science-and-it-practice.pdf»
Если все сделаете правильно, по ссылке выше будет открываться правильная страница в правильном PDFе.
Ну и наконец, вики-разметкой напишите ваше понимание, почему правильный ответ — правильный, а неправильные варианты — неправильны.
Тут тоже могут быть полезны ссылки на википедию, решение вами рекуррентных уравнений в sympy.
Задача зарезервирована: StasFomin 20:47, 24 декабря 2024 (UTC)
Задача «2019-gate-computer-science-and-it-practice.pdf/Q05-alg1»
Вопрос: Q05-alg1-31d68c
Вопрос из «Algorithms Test 1» где-то со страницы 222.
Тут вставьте перевод вопроса.
Используйте возможности разметки, включая формулы и т.п, если будут графы — посмотрите как задать их текстом https://wiki.4intra.net/Graphviz (реально оценю, полезный навык). Если код — теги «code-pascal», «code-c» или «code-python» (не «source lang»).
В IT вообще не принято писать романы, всегда старайтесь писать структурированные (списками-абзацами тексты). Списки в MediaWiki — это просто «*». Не забывайте о них.
Преформатированный моноширинный текст — просто отступ.
Старайтесь нетривиальные понятия, особенно незнакомые вам, найти ссылку на википедию и вставить (нейросети лажают!).
Это важно, чтобы найти корректный перевод (то, что в википедии, или на худой конец — точно массово гуглится).
Потом конечно сотрите эти инструкции, которые тут курсивом или в блоке цитирования.
Ответы
Если ответы простые, однострочные, используйте простой способ задания ответов списком, типа так (префикс «Правильный ответ:» — это дословно, для правильного ответа, неважно, какой он будет в списке)
- Правильный ответ: тут реально правильный ответ
- неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
Если ответы длинные, многострочные, или там графы, используйте способ задания ответов разделами, Но такое очень редко встречается, например 2011-gre-cs-practice-book.pdf/Q05.
Объяснение
Сначала заполните номер страницы с этим вопросом Исходники — вопрос 5 на тут-номер-страницы-с-вопросом-5 странице книги «2019-gate-computer-science-and-it-practice.pdf»
Если все сделаете правильно, по ссылке выше будет открываться правильная страница в правильном PDFе.
Ну и наконец, вики-разметкой напишите ваше понимание, почему правильный ответ — правильный, а неправильные варианты — неправильны.
Тут тоже могут быть полезны ссылки на википедию, решение вами рекуррентных уравнений в sympy.
Задача зарезервирована: StasFomin 20:47, 24 декабря 2024 (UTC)
Задача «2019-gate-computer-science-and-it-practice.pdf/Q07-alg1»
Вопрос: Q07-alg1-31d68c
Вопрос из «Algorithms Test 1» где-то со страницы 222.
Тут вставьте перевод вопроса.
Используйте возможности разметки, включая формулы и т.п, если будут графы — посмотрите как задать их текстом https://wiki.4intra.net/Graphviz (реально оценю, полезный навык). Если код — теги «code-pascal», «code-c» или «code-python» (не «source lang»).
В IT вообще не принято писать романы, всегда старайтесь писать структурированные (списками-абзацами тексты). Списки в MediaWiki — это просто «*». Не забывайте о них.
Преформатированный моноширинный текст — просто отступ.
Старайтесь нетривиальные понятия, особенно незнакомые вам, найти ссылку на википедию и вставить (нейросети лажают!).
Это важно, чтобы найти корректный перевод (то, что в википедии, или на худой конец — точно массово гуглится).
Потом конечно сотрите эти инструкции, которые тут курсивом или в блоке цитирования.
Ответы
Если ответы простые, однострочные, используйте простой способ задания ответов списком, типа так (префикс «Правильный ответ:» — это дословно, для правильного ответа, неважно, какой он будет в списке)
- Правильный ответ: тут реально правильный ответ
- неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
Если ответы длинные, многострочные, или там графы, используйте способ задания ответов разделами, Но такое очень редко встречается, например 2011-gre-cs-practice-book.pdf/Q05.
Объяснение
Сначала заполните номер страницы с этим вопросом Исходники — вопрос 7 на тут-номер-страницы-с-вопросом-7 странице книги «2019-gate-computer-science-and-it-practice.pdf»
Если все сделаете правильно, по ссылке выше будет открываться правильная страница в правильном PDFе.
Ну и наконец, вики-разметкой напишите ваше понимание, почему правильный ответ — правильный, а неправильные варианты — неправильны.
Тут тоже могут быть полезны ссылки на википедию, решение вами рекуррентных уравнений в sympy.
Задача зарезервирована: StasFomin 20:47, 24 декабря 2024 (UTC)
Задача «2019-gate-computer-science-and-it-practice.pdf/Q01-alg1»
Вопрос: Q01-alg1-31d68c
Вопрос из «Algorithms Test 1» где-то со страницы 222.
Тут вставьте перевод вопроса.
Используйте возможности разметки, включая формулы и т.п, если будут графы — посмотрите как задать их текстом https://wiki.4intra.net/Graphviz (реально оценю, полезный навык). Если код — теги «code-pascal», «code-c» или «code-python» (не «source lang»).
В IT вообще не принято писать романы, всегда старайтесь писать структурированные (списками-абзацами тексты). Списки в MediaWiki — это просто «*». Не забывайте о них.
Преформатированный моноширинный текст — просто отступ.
Старайтесь нетривиальные понятия, особенно незнакомые вам, найти ссылку на википедию и вставить (нейросети лажают!).
Это важно, чтобы найти корректный перевод (то, что в википедии, или на худой конец — точно массово гуглится).
Потом конечно сотрите эти инструкции, которые тут курсивом или в блоке цитирования.
Ответы
Если ответы простые, однострочные, используйте простой способ задания ответов списком, типа так (префикс «Правильный ответ:» — это дословно, для правильного ответа, неважно, какой он будет в списке)
- Правильный ответ: тут реально правильный ответ
- неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
Если ответы длинные, многострочные, или там графы, используйте способ задания ответов разделами, Но такое очень редко встречается, например 2011-gre-cs-practice-book.pdf/Q05.
Объяснение
Сначала заполните номер страницы с этим вопросом Исходники — вопрос 1 на тут-номер-страницы-с-вопросом-1 странице книги «2019-gate-computer-science-and-it-practice.pdf»
Если все сделаете правильно, по ссылке выше будет открываться правильная страница в правильном PDFе.
Ну и наконец, вики-разметкой напишите ваше понимание, почему правильный ответ — правильный, а неправильные варианты — неправильны.
Тут тоже могут быть полезны ссылки на википедию, решение вами рекуррентных уравнений в sympy.
Задача зарезервирована: StasFomin 20:47, 24 декабря 2024 (UTC)
Задача «2001-gre-vs-practice.pdf/Q27»
Вопрос: Q27-e5724f
Тут вставьте перевод вопроса. Используйте возможности разметки, включая формулы и т.п, если будут графы — посмотрите как задать их текстом https://wiki.4intra.net/Graphviz (реально оценю, полезный навык). Если код — теги «code-pascal», «code-c» или «code-python» (не «source lang»).
В IT вообще не принято писать романы, всегда старайтесь писать структурированные (списками-абзацами тексты). Списки в MediaWiki — это просто «*». Не забывайте о них.
Преформатированный моноширинный текст — просто отступ.
Старайтесь нетривиальные понятия, особенно незнакомые вам, найти ссылку на википедию и вставить (нейросети лажают!).
Это важно, чтобы найти корректный перевод (то, что в википедии, или на худой конец — точно массово гуглится).
Потом конечно сотрите эти инструкции, которые тут курсивом или в блоке цитирования.
Ответы
Если ответы простые, однострочные, используйте простой способ задания ответов списком, типа так (префикс «Правильный ответ:» — это дословно, для правильного ответа, неважно, какой он будет в списке)
- Правильный ответ: тут реально правильный ответ
- неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
Если ответы длинные, многострочные, или там графы, используйте способ задания ответов разделами, Но такое очень редко встречается, например 2011-gre-cs-practice-book.pdf/Q05.
Объяснение
Сначала заполните номер страницы с этим вопросом Исходники — вопрос 27 на тут-номер-страницы-с-вопросом-27 странице книги «2001-gre-vs-practice.pdf»
Если все сделаете правильно, по ссылке выше будет открываться правильная страница в правильном PDFе.
Ну и наконец, вики-разметкой напишите ваше понимание, почему правильный ответ — правильный, а неправильные варианты — неправильны.
Тут тоже могут быть полезны ссылки на википедию, решение вами рекуррентных уравнений в sympy.
Задача зарезервирована: KoshelevEA 06:21, 8 января 2025 (UTC)
Задача «2001-gre-vs-practice.pdf/Q20»
Вопрос: Q20-e5724f
Задача зарезервирована: илья52 10:57, 21 декабря 2024 (UTC)
Тут вставьте перевод вопроса. Используйте возможности разметки, включая формулы и т.п, если будут графы — посмотрите как задать их текстом https://wiki.4intra.net/Graphviz (реально оценю, полезный навык). Если код — теги «code-pascal», «code-c» или «code-python» (не «source lang»).
В IT вообще не принято писать романы, всегда старайтесь писать структурированные (списками-абзацами тексты). Списки в MediaWiki — это просто «*». Не забывайте о них.
Преформатированный моноширинный текст — просто отступ.
Старайтесь нетривиальные понятия, особенно незнакомые вам, найти ссылку на википедию и вставить (нейросети лажают!).
Это важно, чтобы найти корректный перевод (то, что в википедии, или на худой конец — точно массово гуглится).
Потом конечно сотрите эти инструкции, которые тут курсивом или в блоке цитирования.
Ответы
Если ответы простые, однострочные, используйте простой способ задания ответов списком, типа так (префикс «Правильный ответ:» — это дословно, для правильного ответа, неважно, какой он будет в списке)
- Правильный ответ: тут реально правильный ответ
- неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
Если ответы длинные, многострочные, или там графы, используйте способ задания ответов разделами, Но такое очень редко встречается, например 2011-gre-cs-practice-book.pdf/Q05.
Объяснение
Сначала заполните номер страницы с этим вопросом Исходники — вопрос 20 на тут-номер-страницы-с-вопросом-20 странице книги «2001-gre-vs-practice.pdf»
Если все сделаете правильно, по ссылке выше будет открываться правильная страница в правильном PDFе.
Ну и наконец, вики-разметкой напишите ваше понимание, почему правильный ответ — правильный, а неправильные варианты — неправильны.
Тут тоже могут быть полезны ссылки на википедию, решение вами рекуррентных уравнений в sympy.
Задача «2001-gre-vs-practice.pdf/Q12»
Вопрос: Q12-e5724f
Определение для «word» в БНФ дано следующими правилами:
- I. word
- II. words
- III. c22
Ответы
- Ни одного
- Только I и II
- Только I и III
- Правильный ответ: Только II и III
- I, II и III
Объяснение
Исходники — вопрос 12 на 18 странице книги «2001-gre-vs-practice.pdf»
Проверка утверждений:
I. `word` состоит из 4 букв. Посмотрим, можно ли это получить из <word>:
II. `words` состоит из 5 букв. Посмотрим, можно ли это получить из <word>:
Задача зарезервирована: ZharovG 16:13, 20 декабря 2024 (UTC)
Задача «2011-gre-cs-practice-book.pdf/Q68»
Вопрос: Q68-08c765
Тут вставьте перевод вопроса. Используйте возможности разметки, включая формулы и т.п, если будут графы — посмотрите как задать их текстом https://wiki.4intra.net/Graphviz . Если код — теги «code-pascal», «code-c» или «code-python».
Старайтесь нетривиальные понятия, особенно незнакомые вам, найти ссылку на википедию и вставить (нейросети лажают!).
Это важно, чтобы найти корректный перевод (то, что в википедии, или на худой конец — точно массово гуглится).
Потом конечно сотрите инструкции, которые тут курсивом.
Ответы
Если ответы простые, однострочные, используйте простой способ задания ответов списком, типа так (префикс «Правильный ответ:» — это дословно, для правильного ответа, неважно, какой он будет в списке)
- Правильный ответ: тут реально правильный ответ
- неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
- еще какой-то неправильный ответ
Если ответы длинные, многострочные, или там графы, используйте способ задания ответов разделами, Но такое очень редко встречается.
Объяснение
Сначала заполните номер страницы с этим вопросом Исходники — вопрос 68 на тут-номер-страницы-с-вопросом-68 странице книги «2011-gre-cs-practice-book.pdf»
Если все сделаете правильно, по ссылке выше будет открываться правильная страница в правильном PDFе.
Ну и наконец, вики-разметкой напишите ваше понимание, почему правильный ответ — правильный, а неправильные варианты — неправильны.
Тут тоже могут быть полезны ссылки на википедию, решение вами рекуррентных уравнений в sympy.
Задача зарезервирована: Nikitashapovalov 20:45, 8 января 2025 (UTC)
Задача «2011-gre-cs-practice-book.pdf/Q63»
Вопрос: Q63-08c765
Алгоритм берет список из
Предположим, что элементы исходного списка — целые числа от 1 до 64 в случайном порядке. Какова вероятность того, что число 63 появится в финальном списке из двух элементов?
Ответы
-
\frac{1}{63} -
\frac{1}{4} - Правильный ответ:
\frac{32}{63} -
\frac{62}{63} -
1
Объяснение
Исходники — вопрос 63 на 44 странице книги «2011-gre-cs-practice-book.pdf»
Задача зарезервирована: Nikitashapovalov 20:51, 8 января 2025 (UTC)
Задача «2011-gre-cs-practice-book.pdf/Q38»
Задача зарезервирована: Yaroslav Klimov М05-304Б 06:09, 21 декабря 2024 (UTC)
Вопрос: Q38-08c765
Рассмотрим три процесса P1, P2, и P3, с моментами прихода 0 ms, 10 ms, и 20 ms, соответственно, и временем обработки 30 ms, 15 ms, 30 ms.
Все три процесса планируются в системе с 1 ядром, с использованием политики Shortest Remaining Processing Time First (SRPT) — наименьшее оставшееся время обработки.
В каком порядке процессы завершатся (от первого до последнего)?
Ответы
- P1, P2, P3
- P1, P3, P2
- Правильный ответ: P2, P1, P3
- P2, P3, P1
- P3, P1, P2
Объяснение
Исходники — вопрос 38 на 33 странице книги «2011-gre-cs-practice-book.pdf»
SRPT (Shortest Remaining Processing Time First):
- Приоритет отдаётся процессу с наименьшим оставшимся временем обработки.
- Если приходит новый процесс с меньшим оставшимся временем, текущий процесс прерывается.
Таймлайн выполнения процессов:
- Время 0 ms:
- P1 доступен, запускается.
- Активный процесс: P1 (оставшееся время = 30 ms).
- Время 10 ms:
- P2 приходит (время обработки = 15 ms).
- P2 имеет меньшее оставшееся время, чем P1, поэтому P1 прерывается, и запускается P2.
- Активный процесс: P2 (оставшееся время = 15 ms).
- Время 20 ms:
- P3 приходит (время обработки = 30 ms).
- P2 всё ещё имеет меньшее оставшееся время, чем P1 и P3, поэтому P2 продолжает выполнение.
- Активный процесс: P2.
- Время 25 ms:
- P2 завершает выполнение.
- Следующий процесс — P1, так как его оставшееся время (25 ms) меньше, чем у P3 (30 ms).
- Активный процесс: P1.
- Время 55 ms:
- P1 завершает выполнение.
- Остался только P3.
- Активный процесс: P3.
- Время 85 ms:
- P3 завершает выполнение.
Порядок завершения:
Первым завершается P2 (25 ms).
Затем P1 (55 ms).
Последним P3 (85 ms).
Задача «Optprob/Проект киносьемки»
В следующей таблице перечислены мероприятия, на которые делится кинопроект, их продолжительность в днях и зависимости предшествования.
Код | Суть работы | Зависит | Длительность
a | Написать сценарий | | 30 b | Найти местность для сьемки на воздухе | a | 10 c | Получить у местных властей разрешение | b | 10 d | Подбор интерьеров для внутренних сьемок| a | 8 e | Кастинг актеров | a | 10 f | Нанять технический персоналa | a | 8 g | Размещение актеров и техперсонала | ef | 1 h | Костюмы | e | 5 i | Съемка на местности без актеров | cf | 1 j | Съемки с актерами | ihgd | 5
- Визуализируйте граф работ
- Найдите критические пути и ожидаемую продолжительность проекта.
Задача зарезервирована: Vsevolodpl 13:48, 6 января 2025 (UTC)
Задача «Optprob/Оптимизация медицинских служб»
Задача зарезервирована: AlferovIS 14:10, 1 декабря 2024 (UTC)
Три медицинские службы состоят из 10, 6 и 4 врачей соответственно; каждый врач принимает максимум 10 пациентов.
Стоимость лечения каждого пациента составляет
- 10 евро в день для службы 1,
- 20 евро в день для службы 2,
- 25 евро в день для службы 3.
Общий дневной бюджет для трех служб составляет 2400 евро.
Кроме того, первые две службы должны обслуживать как минимум в два раза больше пациентов, чем служба 3.
- Сценарий 1
Сколько пациентов должно приниматься ежедневно в каждой службе, с целью максимизации общего количества принятых людей.
- Сценарий 2
Дневной бюджет был увеличен до €3200.
Больница должна принять решение: открыть четвертую медицинскую службу с 5 новыми врачами и стоимостью обслуживания одного пациента 22 €/день или увеличить каждую из существующих служб на два врача.
Определите, какое решение принять, с целью максимизации общего количества принятых пациентов.
Задача «Optprob/Три изделия на двух из четырех станков»
Предприниматель, производящий три изделия P1, P2, P3, хочет найти дневной объем производства, который позволит ему максимизировать прибыль.
- Эти изделия обрабатываются на двух из четырех имеющихся в его распоряжении станков, либо A и B, либо C и D.
- Количество часов работы каждой машины составляет 190, 210, 170 и 200 соответственно.
- Постоянные дневные затраты на запуск каждого из этих станков составляют 20, 25, 35 и 15 денежных единиц соответственно.
- Доход от этих изделий составляет 5 денежных единиц на единицу изделия P1, 5 денежных единиц на единицу изделия P2 и 10 денежных единиц на единицу изделия P3.
- На каждую единицу станка и изделия необходимо затратить следующие часы:
- Максимизируйте общую дневную прибыль.
Вариация:
- Добавьте ограничение, что при производстве товара P1 должно быть произведено не менее 10 единиц и не более 20 единиц товара P2 и не менее 5 единиц товара P1.
Задача зарезервирована: Vsevolodpl 23:32, 8 января 2025 (UTC)
Задача «MAX-CUT: вероятностное округление/Задачи/eupce-6-20»
Задача зарезервирована: илья52 21:49, 19 декабря 2024 (UTC)
Задача «MAX-CUT: вероятностное округление/Задачи/eupce-6-17»
Проверено: StasFomin 09:07, 27 ноября 2024 (UTC)
Задача зарезервирована: LunevLA 19:21, 25 ноября 2024 (UTC)
Задача «MAX-SAT: дерандомизация/Задачи/eupce-6-15»
Задача зарезервирована: EjenY 15:43, 10 ноября 2024 (UTC)
Задача «MAX-CUT: вероятностное округление/Задачи/eupce-6-14»
Задача зарезервирована: илья52 21:25, 19 декабря 2024 (UTC)
Задача «MAX-CUT: вероятностное округление/Задачи/eupce-6-11»
Задача зарезервирована: AlferovIS 20:54, 1 декабря 2024 (UTC)
Задача «MAX-CUT: вероятностное округление/Задачи/eupce-6-10»
Задача зарезервирована: Trifonov.dv 19:15, 15 декабря 2024 (UTC)
Задача «MAX-CUT: вероятностное округление/Задачи/eupce-6-9»
Задача зарезервирована: илья52 21:50, 19 декабря 2024 (UTC)
Задача «MAX-CUT: вероятностное округление/Задачи/eupce-6-8»
Задача зарезервирована: Конин Георгий 20:59, 3 декабря 2024 (UTC)
Задача «MAX-CUT: вероятностное округление/Задачи/eupce-6-7»
Задача зарезервирована: Glbmkrv 02:35, 15 декабря 2024 (UTC)
Задача «MAX-SAT: вероятностное округление/Задачи/eupce-6-3-a»
Проверено: StasFomin 22:42, 17 декабря 2024 (UTC)
- Дан n-вершинный неориентированный граф G=(V, E).
Рассмотрим следующий метод генерации независимого множества.
Для заданной перестановки вершин σ, определим подмножество S(σ) вершин следующим образом: для каждой вершины i, i ∈ S(σ) тогда и только тогда, когда ни один сосед j вершины i не предшествует i в перестановке σ.
Покажите, что каждый S(σ) будет независимым множеством в G.
Задача зарезервирована: Конин Георгий 10:48, 13 декабря 2024 (UTC)
Задача «MAX-SAT: вероятностное округление/Задачи/eupce-6-1-a»
Рассмотрим K-ESAT, SAT, когда в каждой скобке ровно k литералов.
Предложите Лас-Вегас алгоритм выполняющий минимум
Задача зарезервирована: NikitaAkshaev 11:28, 18 декабря 2024 (UTC)
Задача «Вероятность/Задачи/eupce-2-13-b»
Решите обобщенную версию задачи [[../eupce-2-13]]:
- kn различных купонов, организованных в n непересекающихся наборов из k купонов.
- нужен один купон из каждого набора.
Задача зарезервирована: MordashovAP 14:41, 20 декабря 2024 (UTC)
Задача «Вероятность/Задачи/eupce-2-13»
- Каждая коробка хлопьев содержит один из 2n различных купонов (купон в каждой коробке выбирается независимо и равномерно случайным образом из 2n).
- Купоны организованы в n пар, так что купоны 1 и 2 составляют пару, купоны 3 и 4 составляют пару и так далее.
- Получив по одному купону из каждой пары, вы можете получить приз.
Какое ожидаемое количество коробок, надо для этого купить?
Задача зарезервирована: AlferovIS 16:11, 1 декабря 2024 (UTC)
Задача «Вероятность/Задачи/eupce-2-9»
Задача зарезервирована: Галлямов Ислам М05-304б 13:43, 9 декабря 2024 (UTC)
Дважды бросают честный k-гранный кубик с числами от 1 от k до k на гранях кубика, получая значения X1 и X2.
- E[max(X1, X2)] = ?
- E[min(X1, X2)] = ?
Покажите, что E[max(X1 , X2)] + E[min(X1 , X2)] = E[X1] + E[X2].
Задача «Вероятность/Задачи/eupce-2-8-a»
Алиса и Боб решили заводить детей до тех пор, пока у них не родится девочка или пока у них не будет k ≥ 1 детей.
Предположим, что каждый ребенок будет мальчиком или девочкой независимо с вероятностью 1/2 и что многоплодных родов не бывает.
- Каково ожидаемое число детей женского пола?
- Каково ожидаемое число детей мужского пола?
Задача зарезервирована: LunevLA 15:45, 23 ноября 2024 (UTC)
Задача «Вероятность/Задачи/eupce-2-7-c»
Задача зарезервирована: Solovev 15:16, 10 ноября 2024 (UTC)
X и Y — независимые случайные величины с геометрическим распределением, с параметрами P и Q соответственно.
P(min(X, Y) = k) = ?
Задача «Вероятность/Задачи/eupce-2-7-a»
X и Y — независимые случайные величины с геометрическим распределением, с параметрами P и Q соответственно.
P(X = Y) = ?
Задача зарезервирована: Галлямов Ислам М05-304б 15:36, 13 декабря 2024 (UTC)
Задача «Вероятность/Задачи/eupce-2-6-d»
Предположим, что независимо бросают два стандартных шестисторонних кости, X1 — то, что выпадает на первой, X2 — на второй, а X — сумма обоих значений.
- 2 ≤ k ≤ 12
- E[X1 - X2 | X = k] = ?
Задача зарезервирована: RomanFilonov 20:42, 8 декабря 2024 (UTC)
Задача «Вероятность/Задачи/eupce-2-6-c»
Предположим, что независимо бросают два стандартных шестисторонних кости, X1 — то, что выпадает на первой, X2 — на второй, а X — сумма обоих значений.
E[X1 | X = 9] = ?
Задача зарезервирована: AlferovIS 16:19, 1 декабря 2024 (UTC)
Задача «Вероятность/Задачи/eupce-2-6-b»
Предположим, что независимо бросают два стандартных шестисторонних кости, X1 — то, что выпадает на первой, X2 — на второй, а X — сумма обоих значений.
E[X | X1 = X2] = ?
Задача зарезервирована: LunevLA 15:06, 25 ноября 2024 (UTC)
Задача «Вероятность/Задачи/eupce-2-5»
Если X — случайная величина с биномиальным распределением B(n, 1/2) для n ≥ 1, покажите, что вероятность того,
что X — четное будет 1/2.
Задача зарезервирована: AlferovIS 16:09, 1 декабря 2024 (UTC)
Задача «Вероятность/Задачи/eupce-2-4»
Докажите, что
Задача зарезервирована: Ermakov
Задача «Вероятность/Задачи/eupce-1-26-b»
Обычные крестики-нолики скучные, при оптимальной стратегии в них выигрывают крестики.
Рассмотрим вероятную модификацию этой игры.
- Как обычно, крестики и нолики ходят по очереди и нолик идет первым. Как обычно, выигрывает тот, кто первый добъется «три в ряд», или ничья, если никто.
- Но на каждом ходе позиция и у крестиков и у ноликов выбирается независимо и равномерно среди свободных квадратов.
Найдите вероятность, выигрыша для «крестиков» и для «ноликов».
Задача зарезервирована: MordashovAP 12:33, 19 декабря 2024 (UTC)
Задача «Вероятность/Задачи/eupce-1-26-a»
Задача зарезервирована: Ydanyok 09:03, 13 декабря 2024 (UTC)
Обычные крестики-нолики скучные, при оптимальной стратегии в них выигрывают крестики. Рассмотрим вероятную модификацию этой игры.
- Изначально, бросая честную монетку, разметим каждый из девяти квадратов либо X, либо O.
- Если только один из игроков имеет «три в ряд» → он победил.
- Если оба или никто → ничья.
Определите вероятность, что «X» выиграет.
Задача «Вероятность/Задачи/eupce-1-16-d»
Задача зарезервирована: илья52 21:49, 19 декабря 2024 (UTC)
Рассмотрим игру, основанную на бросках трех стандартных шестисторонних костей. Цель → получить одинаковое число на всех трех костях, кто первый этого добьется, тот выиграл.
- Игрок начинает с броска всех трех кубиков.
- После первого броска игрок может выбрать одну, две или три кости и бросить их снова.
- После второго броска игрок один из трех кубиков и перебросить его.
Предположим, что игрок использует следующую оптимальную стратегию:
- если все три кости одинаковые → останавливаемся и выигрываем;
- если два кубика совпадают, игрок перебрасывает тот, который «выбивается из коллектива».
- если все не совпадают — перебрасываем их всех.
Рассматривая все возможные возможные выпадения костей, найдите вероятность того, что игрок выиграет.
Задача «Вероятность/Задачи/eupce-1-16-a»
Рассмотрим игру, основанную на бросках трех стандартных шестисторонних костей.
Цель → получить одинаковое число на всех трех костях, кто первый этого добьется, тот выиграл.
- Игрок начинает с броска всех трех кубиков.
- После первого броска игрок может выбрать одну, две или три кости и бросить их снова.
- После второго броска игрок один из трех кубиков и перебросить его.
Предположим, что игрок использует следующую оптимальную стратегию:
- если все три кости одинаковые → останавливаемся и выигрываем;
- если два кубика совпадают, игрок перебрасывает тот, который «выбивается из коллектива».
- если все не совпадают — перебрасываем их всех.
Найдите вероятность того, что все три кубика показывают одинаковое число в первом броске.
Задача зарезервирована: MordashovAP 12:37, 19 декабря 2024 (UTC)
Задача «Вероятность/Задачи/eupce-1-15»
Предположим, что бросают десять стандартных шестисторонних костей.
Какова вероятность того, что их сумма будет деленной на 6, предполагая, что броски независимы?
Задача зарезервирована: Ermakov
Задача «Вероятность/Задачи/eupce-1-14»
Задача зарезервирована: Ydanyok 15:32, 13 декабря 2024 (UTC)
Я играю в турнире ракетбола против игрока, против которого раньше не играл, но видел его в игре.
Априори рассматриваю три равновероятные возможности:
- мы одинаково талантливы, каждый из нас в равной степени может выиграть каждую игру;
- Я немного лучше, и поэтому я выигрываю каждую игру независимо с вероятностью 0.6;
- Он немного лучше, и поэтому он выигрывает каждую игру независимо с вероятностью 0.6.
В рокетбол играют, пока один игрок не выиграет три сета. В нашей игре, я выиграл только второй сет, а противник выиграл первый, третий и четвертый.
В апостеорной модели, с какой вероятностью я должен верить, что мой оппонент немного лучше, чем я?
Задача «Вероятность/Задачи/eupce-1-13»
Медицинская компания рекламирует свой новый тест на определенное заболевание.
Частота ошибок первого рода (false negative) мала: если у вас есть расстройство, вероятность того, что тест вернет положительный результат, составляет 0.999.
Частота ошибок второго рода (false positive) тоже невелика: если у вас нет расстройства, вероятность того, что тест вернет положительный результат, составляет всего 0.005.
Предположим, что эту болезнь имеет 2% населения.
Если мы проверяем человека, выбранного равномерно из популяции, и получается положительный результат, какова вероятность того, что эта болезнь у него действительно есть?
Задача зарезервирована: Ermakov
Задача «Вероятность/Задачи/eupce-1-11-c»
Пытаемся передать один бит (0 или 1) через «n» промежуточных узлов, каждый из которых независимо
может инвертировать бит с вероятностью «p».
Докажите, что вероятность получения корректного бита:
\frac{1+(1-2p)^n}{2}
Задача зарезервирована: RomanFilonov 19:10, 8 декабря 2024 (UTC)
Задача «Вероятность/Задачи/eupce-1-9»
- Честную монету бросили «n» раз.
- Для k>0, найдите верхнюю границу вероятности, что будет последовательность из
\log_2 n + k последовательных орлов.
Задача зарезервирована: RomanFilonov 15:46, 8 декабря 2024 (UTC)
Задача «Open Exercises»
Задача «Hardprob/Minimum Sum Of Squares»
- Конечное множество A, задан размер
s(a)∈ Z^+ для каждого a ∈ A, и целое K ≥ 2 . - Найти разбиение A на множество из K непересекающихся множеств A1, A2, …, AK.
- Минимизировать сумму квадратов их размеров
\begin{displaymath}
\sum_{i=1}^{K}\left(\sum_{a∈ A_i} s(a)\right)^2 → \min. \end{displaymath}
Код в «minimum-sum-of-squares.ipynb» на гитлаб или живьем в лабе
-
 — есть тестовые данные и визуализация.
— есть тестовые данные и визуализация. -
 — есть Pyomo-формулировка для ЦЛП.
— есть Pyomo-формулировка для ЦЛП.
- Но надо проверять и рефакторить.
Задача зарезервирована: StasFomin 20:22, 21 мая 2025 (UTC)
- Задача в базе NP-полных задач Вигго Кана
- Код задачи в книге «ГД» → «SP19»
Задача «Hardprob/Minimum Test Collection»
- Коллекция C подмножеств конечного множества S.
- Найти подколлекцию C'⊆ C, такую, что для каждой пары различных элементов (и для каждого элемента этой пары)
x_1, x_2 ∈ S , есть некоторое подмножествоc∈C' , которое содержит точно один элемент из этой пары. - Минимизировать мощность этой подколлекции |C'|.
Для понимания названия задачи, представим, что S — это множество возможных болезней, а подмножества — это симптомы (или «тесты»), которые могут быть характерны для нескольких болезней. И мы должны выбрать такой набор симптомов-тестов, чтобы имея результаты, мы могли отличить у пациента любые пары болезней.
Код в «minimum-test-collection.ipynb» на гитлаб или живьем в лабе
-
 — есть тестовые данные и визуализация.
— есть тестовые данные и визуализация. -
 — есть Pyomo-формулировка для ЦЛП.
— есть Pyomo-формулировка для ЦЛП. -
 — есть сведение на Python NP-полной задачи к данной.
— есть сведение на Python NP-полной задачи к данной.
- Вроде как все есть, но надо бы прорефакторить решение студента
- Задача в базе NP-полных задач Вигго Кана
- Код задачи в книге «ГД» → «SP6»
Задача зарезервирована: StasFomin 20:35, 21 мая 2025 (UTC)
Задача «Hardprob/Minimum Metric Traveling Salesperson Problem»
- Набор C из m городов с заданными расстояниями между ними
d(c_i,c_j)∈ N для каждой пары городов. Расстояния удовлетворяют неравенству треугольника! - Найти тур C, т.е. перестановка
\pi: [1..m]→ [1..m] . - Минимизировать длину этого тура
d\left(\{c_{\pi(m)},c_{\pi(1)}\}\right)+\displaystyle\sum\limits_{i=1}^{m-1} d\left(\{c_{\pi(i)},c_{\pi(i+1)}\}\right)
Код в «minimum-metric-traveling-salesperson-problem.ipynb» на гитлаб или живьем в лабе
-
 — есть тестовые данные и визуализация.
— есть тестовые данные и визуализация. -
 — есть Pyomo-формулировка для ЦЛП.
— есть Pyomo-формулировка для ЦЛП.
- StasFomin 17:00, 21 мая 2025 (UTC): но надо бы прорефакторить все.
Задача зарезервирована: StasFomin 17:01, 21 мая 2025 (UTC)
Задача «Open Classic Hard Problems»
Задача «Optprob/Планируем генерацию электричества»
Долгосрочный план выработки электроэнергии учитывает график работы существующих энергоблоков и график установки новых электростанций для удовлетворения спроса на электроэнергию в течение ряда будущих (5) лет при минимально возможных затратах.
- Период планирования; 5 лет
Потребность в электроэнергии описывается кривой продолжительности нагрузки (LDC), как показано на рис (цифры на картинке приблизительны, точные будут дальше текстом), по оси ординат — мегаватты, по оси абсцисс — часы.
Площадь под графиком соответствует потребностям производства электроэнергии в мегаватт-часах.
Чтобы модель была простой, например линейной, график аппроксимируется кусочно-постоянной функцией, показанной в виде гистограммы (ступенчатой функции), с
- «Bars=4».
- TD — отсечки по горизонтали
2920 3650 1280 910
Первый столбец обозначает минимальную нагрузку, столбец «4» — пиковую нагрузку, а два промежуточных — представляют потребность в средней нагрузке.
В любой компании или стране для производства электроэнергии используется несколько различных типов (n=5) технологий, таких как
- паровые турбины
- газовые турбины
- гидроэлектростанции
- дизель-генераторы
- комбинированные генераторы
Эти энергоблоки требуют различных затрат, затрат на установку и переменных затрат, и переменная по времени генерации (что-то ломается, что-то амортизируется, что-то улучшается).
- ; — планируемые мощности существующих генерирующих типов по времени.
15000 18000 20000 21000 21000
40000 350000 300000 280000 280000
50000 400000 400000 400000 300000
10000 100000 120000 130000 150000
1000 11000 12000 14000 16000
- ; Переменная (на мегаватт) годовая стоимость старой установки типа «i»
4 4 4 4 4
5 5 5 5 5
3 3 3 3 3
3 3 3 3 3
1 1 1 1 1
Кроме того, в будущем могут быть добавлены дополнительные мощности.
Например, предположим, что модель решила установить новую установку типа «j=1» мощностью 50 МВт в период «1», она будет существовать в системе до истечения технического срока службы этой установки (Это потому, что продолжительность горизонта планирования, рассматриваемого в этой задаче, короче, чем технический срок службы любого нового энергоблока, доступного на рынке).
- ; Фиксированная годовая стоимость новой установки типа «j»
100 110 110 120 120
200 200 200 200 200
300 290 290 285 285
200 190 190 180 180
50 50 50 50 50 ~
- ; Фиксированная годовая стоимость новой установки типа «j»
!AF; 80 80 85 85 85
85 85 85 85 85
90 90 90 90 90
90 90 95 95 95
85 85 90 90 90~
!PD; 6000 6000 6000 6000 6000
9000 10000 110000 12000 13000
25000 27000 27000 27000 27000
50000 58000 58000 58000 57000~
!W; 20 50 10 10 10~
Кроме того, они имеют разный технический срок службы и придерживаются разных правил технического обслуживания.
Задача планирования состоит в том, чтобы определить
- график работы существующих установок,
- установок нового поколения, которые будут запущены в будущем,
- и график введения новых установок путем минимизации суммы затрат на установку и эксплуатацию за заданное количество
лет, соблюдая при этом технические и финансовые ограничения.
Как только будет добавлен новый энергоблок с заданной мощностью, этот энергоблок будет эксплуатироваться на протяжении всего горизонта планирования.
С другой стороны, администрация имеет предпочтение между различными типами технологий, то есть между различными генерирующими установками в случае новых установок.
Это предпочтение описывается процентным коэффициентом от минимума, который должен иметь каждый новый блок, по сравнению с общей энергией, установленной в новых блоках.
Пока не додумано, надо доработать
Задача зарезервирована: StasFomin 16:33, 27 ноября 2022 (UTC)
Задача «Полиномиальные сводимости и NP-полные задачи. Классы NP, coNP, NPC/Задачи/accept-after-t-steps-in-npc»
Задача зарезервирована: Ydanyok 09:10, 13 декабря 2024 (UTC)
- M
- одноленточная машина Тьюринга над бинарным алфавитом.
- t
- число t единичной системе (t единиц).
- Существует вход x, M(x) останавливается и возвращает 1, после t шагов.
Покажите, что это NP-полная задача.
Задача «Введение в теорию вычислимости/Задачи/NP-sums»
Проверить принадлежность классу
Задача зарезервирована: LunevLA 16:01, 23 ноября 2024 (UTC)
Задача «Полиномиальные сводимости и NP-полные задачи. Классы NP, coNP, NPC/Задачи/unary-in-p-then-time2kn-in-time2cn»
Докажите, что если каждый унарный язык из NP также лежит в P, то
то для любого языка из
Задача зарезервирована: Nikitashapovalov 23:51, 19 декабря 2024 (UTC)
Задача «Полиномиальные сводимости и NP-полные задачи. Классы NP, coNP, NPC/Задачи/conp-as-yes»
Покажите, что язык L лежит в co-NP тогда и только тогда, если существует недетерминированная машина M, и полином p, такой, что M останавливается за время p(n) для всех входов x длины n, и L состоит точно только из таких строк x, у которых все пути вычисления M(x) приводят к ответу «1».
Задача зарезервирована: Nikitashapovalov 23:59, 19 декабря 2024 (UTC)
Задача «Полиномиальные сводимости и NP-полные задачи. Классы NP, coNP, NPC/Задачи/DHAM3»
Пусть
-
SHAM_{3} — задача поиска гамильтонового цикла в графеG=(V,E) , где V — делиться на 3. -
DHAM_{3} — задача подтверждения наличия гамильтонового цикла в таком графе.
Докажите, что
Задача зарезервирована: Nikitashapovalov 00:03, 20 декабря 2024 (UTC)
Задача «Полиномиальные сводимости и NP-полные задачи. Классы NP, coNP, NPC/Задачи/MAX-CUT-NPC»
Докажите, что задача MAX-CUT, в форме задачи разрешения («правда, ли, что для графа G есть разрез больше K?») NP-полна.
Задача зарезервирована: Ermakov
Задача «Полиномиальные сводимости и NP-полные задачи. Классы NP, coNP, NPC/Задачи/NTIME-NlogN-reduction-3SAT»
Покажите, что для любого языка
Задача зарезервирована: Nikitashapovalov 00:04, 20 декабря 2024 (UTC)
Задача «Полиномиальная иерархия/Задачи/Свойство Sigma i=PH»
Задача зарезервирована: Nikitashapovalov 23:54, 19 декабря 2024 (UTC)
Задача «Полиномиальная иерархия/Задачи/P^BPP»
Какой класс будет
Задача зарезервирована: NikitaAkshaev 11:40, 18 декабря 2024 (UTC)
Задача «Жадный алгоритм покрытия для почти всех исходных данных/Задачи/Жадное вершинное покрытие для почти всех исходных данных»
Задача зарезервирована: Ydanyok 09:03, 13 декабря 2024 (UTC)
- n-вершин
- ребра между любой парой вершин возникают с вероятностью p.
Какова точность алгоритма для почти всех исходных данных?
(упрощенный вариант — для фиксированного p=½).
Задача «Полиномиальные сводимости и NP-полные задачи. Классы NP, coNP, NPC/Задачи/Квадрат букв»
Задача зарезервирована: илья52 21:51, 19 декабря 2024 (UTC)
Покажите, что следующая задача является NP-полной: дан набор из не более чем $n$ типов квадратиков $1\times1$, на сторонах которых написаны какие-то буквы; дан список допустимых пар букв и список граничных букв; спрашивается, можно ли корректно сложить из квадратиков набора большой квадрат размера $n\times n$ (так, чтобы на примыкающих сторонах квадратиков были только допустимые пары букв, а на границе квадрата~--- только граничные буквы).
- ↑ Т.е. это не как упаковка в многомерном тетрисе
- ↑ Largest Processing Time
- ↑ Largest Processing Time
- ↑ Largest Processing Time