SocialGraphs/Social Random Graphs Models — различия между версиями

Текущая версия на 20:11, 3 апреля 2011

Social Random Graphs Models

Introduction

Recently there has been much interest in studying large-scale real-world networks and attempting to model their properties using random graphs. Although the study of real-world networks as graphs goes back some time, recent activity perhaps started with the paper of Watts and Strogatz [WattsStrogatz1998] about the ‘small-world phenomenon’.

Since then the main focus of attention has shifted to the ‘scale-free’ nature of the networks concerned, evidenced by, for example, power-law degree distributions.

It was quickly observed that the classical models of random graphs introduced by Erdős and Rényi [ErdosRenyi1959] and Gilbert [Gilbert1956] are not appropriate for studying these networks, so many new models have been introduced.

One of the most rapidly growing types of networks are social networks.

Social networks are defined as a set of actors or network members whom are tied by one or more type of relations.

The actors are most commonly persons or organizations however they could be any entities such as web pages, countries, proteins, documents, etc. and sometimes under a more general name, information networks.

There could also be many different types of relationships, to name a few, collaborations, friendships, web links, citations, information flow, etc.

These relations represented by the edges in the network connecting the actors and may have direction (shows the flow from one actor to the other) and strength (shows how much, how often, how important).

Recently, following an interest in studying social networks structure among mathematicians and physicists, researchers investigated statistical properties of networks and methods for modeling networks either analytically or numerically.

It was observed that in many networks the distribution of nodes degrees is highly skewed with a small number of nodes having an unusually large degrees.

Moreover they observed that degree sequences of such networks satisfyied so-called 'power-low'.

This means that the probability of a node to have degree k is equal to , where parameter characterises concrete type of networks.

The work in studying such networks falls very roughly into the following categories.

1. Direct studies of the real-world networks themselves, measuring various properties such as degree-distribution, diameter, clustering, etc.
2. Introdusing new random graph models motivated by this study.
3. Computer simulations of the new models, measuring their properties.
4. Heuristic analysis of the new models to predict their properties.
5. Rigorous mathematical study of the new models in order to prove theorems about their properties.

Although many interesting papers have been written in this area (see, for example, the survey [AlbertBarabasi2002]), so far almost all of this work comes under 1-4. To date there has been little rigorous mathematical work in the field.

In the rest of this chapter we briefly mention the classical models of random graphs and state some results about these models chosen for comparison with recent results about the new models. Then we consider the scale-free models and note that they fall into two types.

The first takes a power-law degree distribution as given, and then generates a graph with this distribution. The second type arises from attempts to explain the power law starting from basic assumptions about the growth of the graph. We will consider models of second type preferably.

We describe

• the Barabási-Albert (BA) model,
• the LCD model, a generalization due to Buckley and Osthus [BuckleyOsthus2001],
• the copying models of Kumar, Raghavan, Rajagopalan, Sivakumar, Tomkins and Upfal [KumarRaghavan2000],
• the very general models defined by Cooper and Frieze [CooperFrieze2003].

Concerning mathematical results we concentrate on the degree distribution, presenting results showing that the models are indeed scale-free and briefly discuss results about properties other than degree sequence: the clustering coefficient, the diameter, and ‘robustness’.

Classical models of random graphs

The theory of random graphs was founded by Erdős and Rényi in a series of papers published in the late 1950s and early 1960s.

Erdős and Rényi set out to investigate what a ‘typical’ graph with n labelled vertices and M edges looks like.

They were not the first to study statistical properties of graphs; what set their work apart was the probabilistic point of view: they considered a probability space of graphs and viewed graph invariants as random variables.

In this setting powerful tools of probability theory could be applied to what had previously been viewed as enumeration questions.

The model of random graphs introduced by Gilbert [Gilbert1956] (precisely at the time that Erdős and Rényi started their investigations) is, perhaps, even more convenient to use.

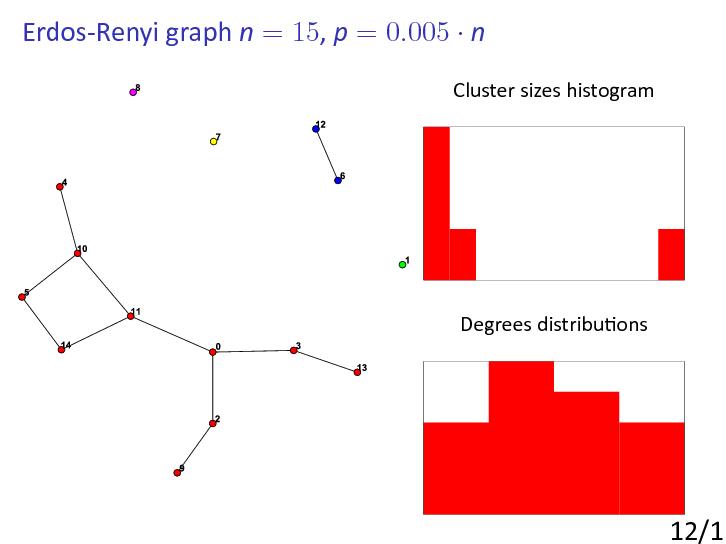
Let G_n,p be the random graph on n nodes in which two nodes i and j are adjacent (connected by an edge) with probability p (independently of all other edges).

So, to construct a random , put in edges with probability p' independently of each other.

It is important that p is often a function of n, though the case p constant, 0 < p < 1, makes perfect sense.

The important study is so-called 'evolution' of random graphs G_n,p that is the study for what functions some parameters or properties of random graphs appear ([ErdosRenyi1960]).

We are interested in what happens as n goes to infinity and we say that G_n,p has a certain property P with high probability (whp) if the probability that G_n,p has this property tends to 1.

For example, it was shown that if then component structure depends on the value of c.

If c < 1 then whp every component of G_n,p has order .

If c > 1 then whp G_n,p has a component with nodes, where a(c) > 0 and all other components have nodes.

Another observation was made for the degree sequence ditribution.

If with c>0 constant the probability of node to have degree k is asyptotically equal to as n goes to infinity (so-called Poisson distribution).

It was proved that in wide range of the diameter of is asymptotic to

.

For many other important properties (connectivity, perfect matchings, hamiltonicity, etc) similar results was proved as well.

Many other interesting results in classical probabilistic models of random graphs can be found in [JansonLuczakRucinski2000].

Watts-Strogatz model

In 1998, Watts and Strogatz [WattsStrogatz1998] raised the possibility of constructing random graphs that have some of the important properties of real-world networks.

The real-world networks they considered included

• neural networks,
• the power grid of the western United States
• the collaboration graph of film actors.

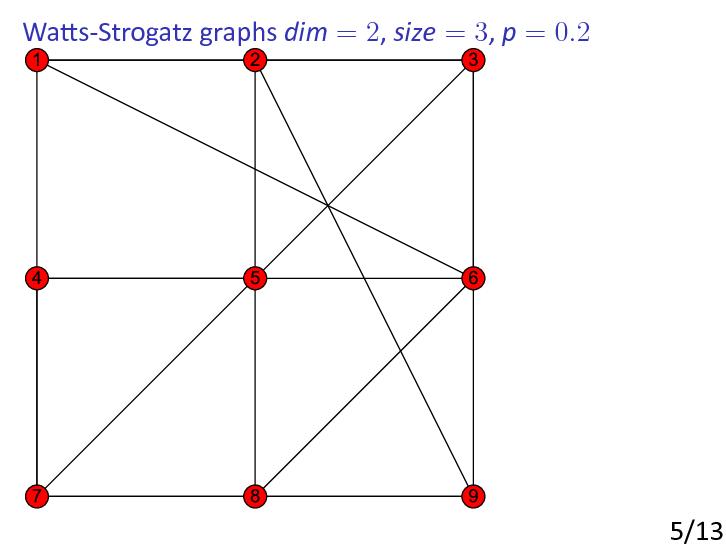
Watts and Strogatz noticed that these networks were ‘small-world’ networks: their diameters were considerably smaller than those of regularly constructed graphs (such as lattices, or grid graphs) with the same number of vertices and edges.

More precisely, Watts and Strogatz found that real-world networks tend to be highly clustered, like lattices, but have small diameters, like random graphs.

That large social networks have rather small diameters had been noticed considerably earlier, in the 1960s, by Milgram [Milgram1967] and others, and was greatly popularized by Guare’s popular play ‘six degrees of separation’ in 1990.

The importance of the Watts and Strogatz paper is due to the fact that it started the active and important field of modelling large-scale networks by random graphs defined by simple rules.

As it happens, from a mathematical point of view, the experimental results in [WattsStrogatz1998] were far from surprising. Instead of the usual diameter diam(G) of a graph G, Watts and Strogatz considered the average distance.

As pointed out by Watts and Strogatz, many real-world networks tend to have a largish clustering coefficient and small diameter. To construct graphs with these properties, Watts and Strogatz suggested starting with a fixed graph with large clustering coefficient and ‘rewiring’ some of the edges. It was shown that introduction of a little randomness makes the diameter small.

Scale-free models

In 1999, Faloutsos, Faloutsos and Faloutsos [Faloutsos1999] suggested certain ‘scale-free’ power laws for the graph of the Internet, and showed that these power laws fit the real data very well.

In particular, they suggested that the degree distribution follows a power law, in contrast to the Poisson distribution for classical random graphs G_n,p.

This was soon followed by work on rather vaguely described random graph models aiming to explain these power laws, and others seen in features of many real-world networks.

In fact, power-law distributions had been observed considerably earlier; in particular, in 1926 Lotka claimed that citations in academic literature follow a power law, and in 1997 Gilbert suggested a probabilistic model supporting Lotka's law.

The degree distribution of the graph of telephone calls seems to follow a power law as well; motivated by this, Aiello, Chung and Lu [AielloChungLu2001] proposed a model for massive graphs.

This model ensures that the degree distribution follows a power law by fixing a degree sequence in advance to fit the required power law, and then taking the space of random graphs with this degree sequence.

The Barabási-Albert model

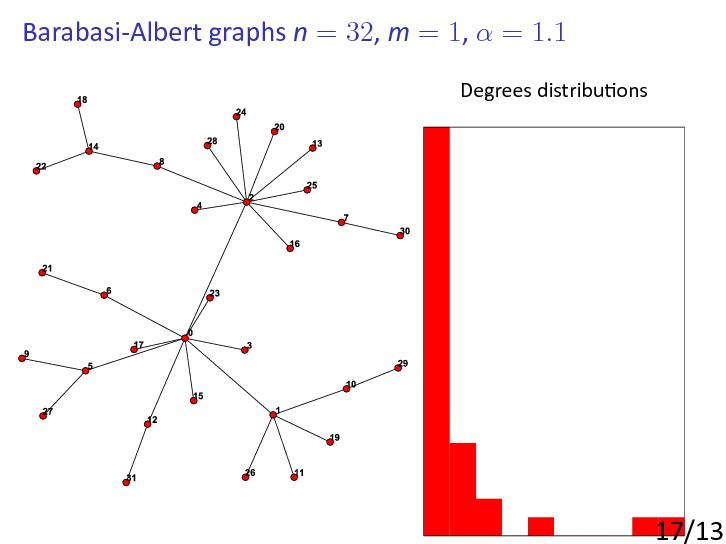
Perhaps the most basic and important of the scale-free random graph models, i.e., models producing power-law or scale-free behaviour from simple rules, is the BA model.

This was introduced by Barabási and Albert in [AlbertBarabasi1999]:

• ... starting with a small number m₀ of vertices,
• at every step we add a new vertex with m edges that link the new vertex to m different vertices

already present in the system assume that the probability P that a new vertex will be connected to a vertex i depends on the connectivity k_i of that vertex, so that .

• After t steps the model leads to a random network with t + m₀ vertices and mt edges.

The basic motivation is to provide a highly simplified model of the growth of, for example, the world-wide web.

New sites (or pages) are added one at a time, and link to earlier sites chosen with probabilities depending on their current popularity — this is the principle that «popularity is attractive».

Barabási and Albert themselves, and many other people, gave experimental and heuristic results about the BA model.

The Buckley-Osthus model

Two groups,

• Dorogovtsev, Mendes and Samukhin [DorogovtsevMendesSamukhin2000]
• Drinea, Enachescu and Mitzenmacher [DrineaEnachescuMitzenmacher2001],

introduced a variation on the BA model in which vertices have an initial attractiveness: the probability that an old vertex is chosen to be a neighbour of the new vertex is proportional to its in-degree plus a constant initial attractiveness, which we shall write as .

The case is just the BA model, since there total degree is used, and each out-degree is m.

The LCD model

The LCD (linearized chord diagram) proposed in [BollobasRiordan2000] has a simple static description and very useful for obtaining mathematical results for scale-free graphs.

In [BollobasRiordan2001] it was proved that random graphs generated according the LCD model are indeed scale-free graphs.

In fact in [BollobasRiordan2004] it was proved that the diameter of scale-free graphs in this model is asymptotically in contrast to known conjecrute (based on experiments) that the diameter is for some constant c.

The copying model

Around the same time as the BA model, Kumar, Raghavan, Rajagopalan, Sivakumar, Tomkins and Upfal [KumarRaghavan2000] gave rather different models to explain the observed power laws in the web graph. The basic idea is that a new web page is often made by copying an old one, and then changing some of the links.

The linear growth copying model is parametrized by a copy factor and a constant out-degree d > 1.

• At each time step, one vertex u is added, and u is then given d out-links for some constant d.
• To generate the out-links, we begin by choosing a prototype vertex p uniformly at random from V_t (the old vertices).

The i-th out-link of u is then chosen as follows.

• With probability α, the destination is chosen uniformly at random from V_t, and with the remaining probability the out-link is taken to be the i th out-link of p.
• Thus, the prototype is chosen once in advance.

The d out-links are chosen by -biased independent coin flips, either randomly from V_t, or by copying the corresponding out-link of the prototype.

The intuition behind this model is the following.

When an author decides to create a new web page, the author is likely to have some topic in mind. The choice of prototype represents the choice of topic—larger topics are more likely to be chosen. The Bernoulli copying events reflect the following intuition: a new viewpoint about the topic will probably link to many pages «within» the topic (i.e., pages already linked to by existing resource lists about the topic), but will also probably introduce a new spin on the topic, linking to some new pages whose connection to the topic was previously unrecognized.

As for the BA model, it was proved that the degree distribution does follow a power law and the probability of node to have degree k is asymptotically

The Cooper-Frieze model

Recently, Cooper and Frieze [CooperFrieze2003] introduced a model with many parameters which includes the last three models as special cases, and proved a very general result about the power-law distribution of degrees. In the undirected case, the model describes a (multi-)graph process G(t), starting from G(0) a single vertex with no edges. Their attachment rule is a mixture of preferential (by degree) and uniform (uniformly at random, or ‘u.a.r’).

Initially, at step t = 0, there is a single vertex . At any step t = 1, 2, ..., T, ... there is a birth process in which either new vertices or new edges are added.

Specifically, either a procedure NEW is followed with probability , or a procedure OLD is followed with probability .

In procedure NEW, a new vertex v is added to G(t − 1) with one or more edges added between v and G(t − 1).

In procedure OLD, an existing vertex v is selected and extra edges are added at v.

The recipe for adding edges typically permits the choice of initial vertex v (in the case of old) and the terminal vertices (in both cases) to be made either u.a.r or according to vertex degree, or a mixture of these two based on further sampling. The number of edges added to vertex v at step t by the procedures (NEW, OLD) is given by distributions specific to the procedure.

The details of these choices are to complicated to be presented here and depend on a lot of parameters.

The results say that the ‘expected degree sequence’ converges in a strong sense to the solution of a certain recurrence relation, and that under rather weak conditions, this solution follows a power law with an explicitly determined exponent and a bound on the error term. Cooper and Frieze also prove a simple concentration result, which we will not state, showing the number of vertices of a certain degree is close to its expectation.

One of the basic properties of the scale-free random graphs considered in many papers is the clustering coefficient C. This coefficient describes ‘what proportion of the acquaintances of a vertex know each other’.

Formally, given a simple graph G (without loops and multiple edges), and a vertex v (with at least two neighbours, say), the local clustering coefficient at v is the number of edges between neighbours of v divided by the number of all possible edges between neighbours of v. The clustering coefficient for the whole graph is the average of local clustering coefficients over all verticies of a graph.

Robustness and vulnerability

Another property of scale-free graphs and the real-world networks inspiring them which has received much attention is their robustness.

Suppose we delete vertices independently at random from G, each with probability q.

• What is the structure of the remaining graph?
• Is it connected?
• Does it have a giant component?

A precise form of the question is: fix 0 < q < 1.

Suppose vertices of G are deleted independently at random with probability q = 1 − p.

Let the graph resulting be denoted G_p.

For which p is there a constant c = c(p) > 0 independent of n such that with high probability G_p has a component with at least cn vertices?

The answer to this natural question was obtained in [BollobasRiordan2003]: with high probability the largest component of G_p has order c(p)n for some constant c(p) > 0.

However, it turns out that this giant component becomes very small as p approaches zero and has order

.

Conclusions

There is a great need for models of real-life networks that incorporate many of the important features of these systems, but can still be analyzed rigorously. The models defined above are too simple for many applications, but there is also a danger in constructing models which take into account too many features of the real-life networks. Beyond a certain point, a complicated model hardly does more than describe the particular network that inspired it. In fact some balance between simplicity of model and correspondence to real-life social networks is needed.

If the right balance can be achieved, well constructed models and their careful analysis should give a sound understanding of growing networks that can be used to answer practical questions about their current state, and, moreover, to predict their future development.

References

• [AielloChungLu2001] W. Aiello, F. Chung and L. Lu, A random graph model for power law graphs, Experiment. Math. 10 (2001), 53-66.
• [AlbertBarabasi2002] R. Albert and A.-L. Barabási, Statistical mechanics of complex networks, Rev. Mod. Phys. 74 (2002), 47-97.
• [AlbertBarabasi1999] A.-L. Barabási and R. Albert, Emergence of scaling in random networks, Science 286 (1999), 509—512.
• [BollobasRiordan2000] B. Bollobas and O.M. Riordan, Linearized chord diagrams and an upper bound for Vassiliev invariants, J. Knot Theory Ramifications 9 (2000), 847-853.
• [BollobasRiordan2003] Bollobas B., Riordan O.M., Robustness and vulnerability of a scale-free random graph, Internet Mathematics, 2003, v. 1, N 1, p. 1-35.
• [BollobasRiordan2004] Bollobas B., Riordan O.M., The diameter of a scale-free random graph, Combinatorica, 2004, v. 24, N 1, p. 5-34.
• [BollobasRiordan2001] B. Bollobas, O. Riordan, J. Spencer and G. Tusn´ady, The degree sequence of a scale-free random graph process, Random Structures and Algorithms 18 (2001), 279—290.
• [BuckleyOsthus2001] Buckley, P.G. and Osthus, D., Popularity based random graph models leading to a scale-free degree sequence, Discrete Mathematics, 2001, volume 282, 53-68
• [CooperFrieze2003] C. Cooper and A. Frieze, A general model of web graphs, Journal Random Structures & Algorithms, Volume 22 Issue 3, May 2003
• [DrineaEnachescuMitzenmacher2001] E. Drinea, M. Enachescu and M. Mitzenmacher, Variations on random graph models for the web, technical report, Harvard University, Department of Computer Science, 2001.
• [DorogovtsevMendesSamukhin2000] S.N. Dorogovtsev, J.F.F. Mendes, A.N. Samukhin, Structure of growing networks with preferential linking Phys. Rev. Lett. 85 (2000), 4633.
• [ErdosRenyi1959] Erdős, P., and Rényi, A., On random graphs I., Publicationes Mathematicae Debrecen 5 (1959), 290—297.
• [ErdosRenyi1960] Erdős, P., and Rényi, A., On the evolution of random graphs, Magyar Tud. Akad. Mat. Kutat´o Int. K¨ozl. 5 (1960), 17-61.
• [Faloutsos1999] M. Faloutsos, P. Faloutsos and C. Faloutsos, On power-law relationships of the internet topology, SIGCOMM 1999, Comput. Commun. Rev. 29 (1999), 251.
• [Gilbert1956] Gilbert, E.N., Enumeration of labelled graphs, Canad. J. Math. 8 (1956), 405—411.
• [JansonLuczakRucinski2000] Janson, S., Luczak, T., and Rucinski, A. (2000). Random Graphs. John Wiley and Sons, New York, xi+ 333pp.
• [KumarRaghavan2000] R. Kumar, P. Raghavan, S. Rajagopalan, D. Sivakumar, A. Tomkins and E. Upfal, Stochastic models for the web graph, FOCS 2000.
• [Milgram1967] Milgram, S., The small world phenomenon, Psychol. Today 2 (1967), 60-67.
• [NewmanStrogatzWatts2001] M.E.J. Newman, S.H. Strogatz and D.J. Watts, Random graphs with arbitrary degree distribution and their applications, Physical Review E 64 (2001), 026118.
• [WattsStrogatz1998] D. J. Watts and S. H. Strogatz, Collective dynamics of small-world networks, Nature 393 (1998), 440—442.
• [NewmanPark2003] M. Newman, J. Park, Why social networks are different from other types of networks, Phys. Rev. E, 2003, v. 68, P036122.
• [LibenNovak2005] D. Liben-Nowell, J. Novak, R. Kumar, P. Raghavan, A. Tomkins, Geographic routing in social networks, Proc. of the National Academy of Sciences, 2005, v. 102(33), p. 11623-11628.