Решенные бизнес задачи
Всего страниц найдено: 31.
----
Задача «Optprob/Транспортировка нефти»
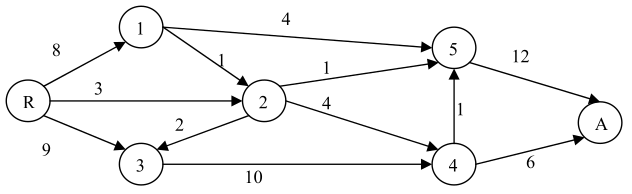
У государственной нефтяной компании есть сеть трубопроводов, по которым она транспортирует нефть с нефтеперерабатывающего завода R в хранилище A, как показано на графе ниже.
Каждая дуга оценивается по максимальному дневному объему, который может быть доставлен, в тысячах литров.
Определите время, необходимое для транспортировки 60000 литров с нефтеперерабатывающего завода в центр хранения, если каждый
день отгружается максимально возможное количество.
Если мощность дуги (2,5) увеличить с 1 до 4, на сколько сократится полученное время?
Задача «Optprob/Производство двух продуктов на трех станках»
Компания производит два продукта A и B, которые обрабатываются на трех станках M1 , M2 и M3. Время обработки в часах каждой единицы продукта на каждом станке, выручка от продажи каждого продукта и недельная готовность каждого станка приведены в следующей таблице:
. A B ЧасовВНеделю
M1 3 5 20
M2 1 10 35
M3 2 8 40
ДоходНаЕдиницу 1000 2000
Компания рассматривает возможность увеличения недельной производительности станка M1 на 10 часов и/или станка M2 на 15 часов и/или станка M3 на 20 часов при затратах в €400, €600 и €500 соответственно (еженедельних).
При этом общие затраты не могут быть больше €1200.
Производительность станка M2 может быть увеличена только при условии увеличения производительности станка M1.
Надо максимизировать прибыль.
Задача «Optprob/Критический путь проекта по графу - 02»
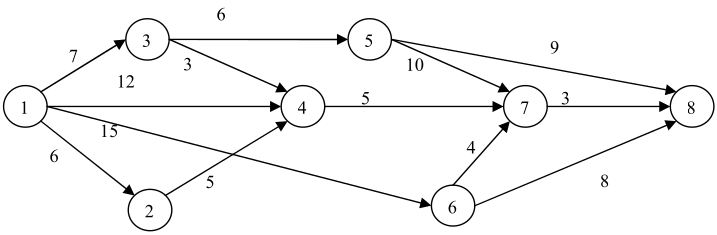
Следующая сеть представляет собой проект, а значения, присвоенные каждой дуге, обозначают продолжительность работ в проекте в днях.
- Определите ожидаемую продолжительность проекта и критический путь, напечатайте таблицу работ с временами начала, окончания, возможностью задержек и т.п.
Задача «Optprob/Художник продает картины галереям»
Престижный художник создал 4 произведения искусства. Галереи A, B и C заинтересованы в их приобретении и готовы заплатить за каждую работу суммы (в миллионах денежных единиц), указанные в таблице:
. Картина1 Картина2 Картина3 Картина4
А 12 10 8 10
B 14 11 6 7
C 15 13 8 9
Художник собирается продать все произведения искусства, и каждая галерея должна приобрести хотя бы одно произведение (им, в общем, все равно, что продадут). Хотя известно, что галерея A купит только одну картину.
Как художник будет распределять произведения искусства между галереями, чтобы максимизировать свой доход?
Вариант: художник добавил следующее ограничение: работы 2 и 4 должны висеть рядом, и быть проданы в одну и ту же галерею.
Задача «Optprob/Оптимизация использования разных станков»
У компании есть два типа станков A и B.
- За каждый час работы на станке A производится 20 деталей, а на станке B — 30 деталей в час.
- В силу возможностей предприятия и всяких рыночных ограничений в день может быть произведено не более 600 и не менее 250 деталей в день.
- Кроме того, из-за характеристик двух станков стоимость единицы продукции, произведенной на станке A, составляет €4, а на станке B — €3.
Определите оптимальное количество часов работы в день для двух станков со следующими целями и приоритетами:
- Приоритет 1. Общая сумма ежедневных расходов не превышает 2000 евро.
- Приоритет 2. Ежедневное рабочее время на станках A и B одинаково.
- Приоритет 3. Максимально увеличить количество изделий в день.
- 📺видео📺
- старая версия 📺видео📺
- Код решения в проекте «adv2022-course-pyomo-business-optimization» в «optprob/Оптимизация_использования_разных_станков.ipynb»
Задача «Optprob/Раздаем задачи сотрудникам, с учетом прошлых оценок»
Менеджер по персоналу компании должен распределить
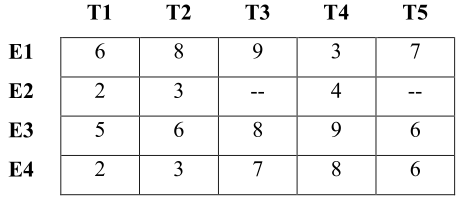
- 5 задач (T1, T2, T3, T4 и T5)
- между 4 сотрудниками (E1, E2, E3 и E4)
- с учетом оценок, сделанных на основе предыдущего опыта, представленного в следующей таблице (0 — плохо, 10 — отлично, "--" никак нельзя давать), надо максимизировать «суммарную оценку»:
Необходимо учитывать следующие ограничения:
- сотрудников нельзя оставлять без задания,
- сотруднику E2 можно поручить только одно задание,
- задания не могут быть общими.
Задача «Optprob/Формируем комиссию в университете»
Университет формирует комиссию. В комиссию были выдвинуты десять человек: A, B, C, D, E, F, G, H, I и J.
Согласно правилам, в комиссию должны войти как минимум одна женщина, один мужчина, один студент,
один администратор и один профессор.
Кроме того, количество женщин должно быть равным количеству мужчин, а количество преподавателей не
должно быть меньше количества административного персонала.
Состав номинантов в следующих категориях выглядит следующим образом:
Категория Лица
Женщины ABCDE
Мужчины FGHIJ
Студенты ABCJ
Административный EF
Учителя DGHI
Комиссия должна быть как можно меньше.
Задача «Optprob/Производство хлеба в пекарне»
Пекарня хочет ввести производство двух новых видов хлеба: цельнозернового и ржаного, поскольку сбыт их продукции гарантирован.
Эти виды хлеба изготавливаются в основном из трех ингредиентов: цельнозерновых отрубей,
пшеничной и ржаной муки.
- Для приготовления 1 кг цельнозернового хлеба требуется 350г цельнозерновых отрубей 150 г пшеничной муки, а для приготовления 1 кг ржаного хлеба — 250 г пшеничной и 250 г ржаной муки.
- Ежедневное наличие цельнозерновых отрубей составляет 210 кг, пшеничной муки — 115 кг, ржаной муки — 100 кг.
- Прибыль на килограмм цельнозернового хлеба составляет 0,40€, а на килограмм ржаного хлеба — 0,60€.
Рассчитайте суточное производство цельнозернового и ржаного хлеба, если в порядке очередности были поставлены следующие задачи:
- Приоритет 1. Желательно, чтобы прибыль составляла не менее 240 евро в день.
- Приоритет 2. Желательно, чтобы количество ежедневно производимого цельнозернового хлеба было как минимум вдвое больше, чем ржаного.
- Приоритет 3. Желательно, чтобы ежедневное количество производимого ржаного хлеба составляло не менее 300 кг.
Какие из предложенных целей могут быть достигнуты?
Задача «Optprob/Планирование производства рождественских игрушек»
Компания по производству игрушек рассматривает возможность выпуска трех новых моделей игрушек для возможного включения в рождественскую кампанию.
- Создание мощностей для производства этих моделей обойдется в €25000, €35000 и €300000
- Прибыль на единицу продукции составит €10, €15 и €13 соответственно.
- У компании есть три завода для производства этих моделей, но, чтобы избежать затрат, только один из них будет производить игрушки, выбор зависит от максимизации прибыли.
Количество человеко-часов, необходимых для производства каждой игрушки на каждом заводе, равно:
Завод Игрушка1 Игрушка2 Игрушка3
Завод1 5 4 6 Завод2 4 2 2 Завод3 3 3 3
- Мощность завода в человеко-часах на заводах составляют 500, 600 и 630 часов в день соответственно
- Руководство решило разработать хотя бы одну из трех игрушек.
- На само производство останется 30 дней.
Надо максимизировать общую прибыль.
Задача «Optprob/Распределение предметов между учителями»
Директор школы должен распределить
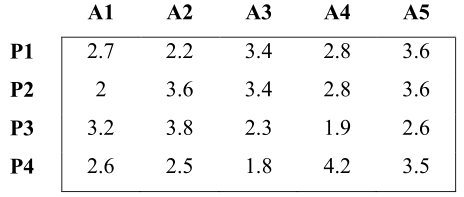
- преподавание 5 предметов, A1, A2, A3, A4 и A5,
- между 4 учителями, P1, P2, P3 и P4,
- принимая во внимание рейтинги опросов учеников и некоторые ограничения, налагаемые МинОбром.
На основе опросов предыдущих лет мы получили следующие средние оценки (шкала: 0 - плохо, 5 - отлично):
Ограничения гласят
- Учитель P3 не может преподавать предметы A1 и A2.
- Учитель P1 должен вести только один предмет.
- Предметы должны преподаваться все.
- Ни один учитель не может остаться без предметов.
Распределите учителей так, чтобы максимизировать среднюю оценку учителя за предмет.
Задача «Optprob/Распределение МРТ по больницам»
Российский олигарх решил пожертвовать E=20 единиц нового технологического оборудования для МРТ (магнитно-резонансной томографии) больницам Московской области, и решено, что каждый житель МО, должен иметь доступ к этим МРТ для диагностики.
В Московской области имеется n=25 государственных больниц.
Количество граждан, относящихся к каждой больнице, известно.
| Больница | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| Район | 1 | 1 | 1 | 2 | 2 | 3 | 3 | 3 | 3 | 4 | 4 | 4 | 4 | 5 | 5 | 5 | 5 | 6 | 6 | 6 | 7 | 7 | 8 | 8 | 8 |
| Граждан | 506500 | 350005 | 275000 | 247156 | 159874 | 236548 | 157489 | 325000 | 259001 | 142000 | 156800 | 247158 | 125698 | 52014 | 69054 | 189456 | 147569 | 458756 | 256478 | 156421 | 152310 | 147150 | 65045 | 89015 | 194520 |
Известно расположение больниц и расстояние между ними.
| |
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 1 | 21 | 23 | 18 | 19 | 12 | 12 | 25 | 72 | 25 | 4 | 25 | 25 | 25 | 18 | 67 | 67 | 67 | 67 | 67 | 25 | 19 | 12 | 12 | 25 | |
| 2 | 0 | 0 | 25 | 5 | 13 | 4 | 4 | 12 | 5 | 12 | 19 | 12 | 12 | 12 | 12 | 75 | 75 | 75 | 75 | 75 | 12 | 13 | 4 | 4 | 12 |
| 3 | 0 | 0 | 0 | 13 | 15 | 19 | 19 | 4 | 9 | 4 | 13 | 4 | 25 | 4 | 25 | 55 | 55 | 55 | 55 | 55 | 4 | 15 | 19 | 19 | 4 |
| 4 | 0 | 0 | 0 | 0 | 59 | 13 | 13 | 19 | 39 | 19 | 15 | 19 | 12 | 19 | 12 | 25 | 25 | 25 | 25 | 25 | 19 | 12 | 13 | 13 | 19 |
| 5 | 0 | 0 | 0 | 0 | 0 | 15 | 15 | 13 | 45 | 13 | 12 | 13 | 12 | 13 | 4 | 12 | 12 | 12 | 12 | 12 | 13 | 12 | 15 | 15 | 13 |
| 6 | 0 | 0 | 0 | 0 | 0 | 0 | 19 | 15 | 23 | 15 | 4 | 15 | 4 | 15 | 19 | 4 | 4 | 4 | 4 | 4 | 15 | 4 | 12 | 12 | 15 |
| 7 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 12 | 22 | 12 | 19 | 12 | 19 | 12 | 13 | 19 | 19 | 19 | 19 | 19 | 12 | 19 | 12 | 19 | 12 |
| 8 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 10 | 4 | 13 | 4 | 13 | 4 | 15 | 4 | 15 | 15 | 4 | 13 | 4 | 13 | 4 | 13 | 4 |
| 9 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 19 | 15 | 19 | 15 | 19 | 12 | 19 | 12 | 12 | 19 | 15 | 19 | 4 | 19 | 15 | 19 |
| 10 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 12 | 13 | 12 | 13 | 4 | 13 | 4 | 4 | 13 | 12 | 13 | 19 | 13 | 12 | 13 |
| 11 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 15 | 4 | 15 | 19 | 15 | 19 | 19 | 15 | 4 | 15 | 13 | 15 | 4 | 15 |
| 12 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 19 | 29 | 13 | 12 | 13 | 13 | 12 | 19 | 12 | 15 | 12 | 19 | 25 |
| 13 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 43 | 15 | 4 | 15 | 15 | 4 | 13 | 4 | 12 | 15 | 13 | 12 |
| 14 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 12 | 19 | 24 | 12 | 19 | 15 | 19 | 4 | 12 | 15 | 4 |
| 15 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 13 | 36 | 4 | 13 | 4 | 13 | 19 | 11 | 78 | 19 |
| 16 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 15 | 19 | 15 | 19 | 15 | 13 | 77 | 49 | 13 |
| 17 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 13 | 32 | 13 | 4 | 15 | 12 | 29 | 15 |
| 18 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 23 | 15 | 19 | 4 | 4 | 43 | 12 |
| 19 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 25 | 13 | 19 | 19 | 9 | 4 |
| 20 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 15 | 13 | 13 | 11 | 19 |
| 21 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 15 | 15 | 12 | 13 |
| 22 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 12 | 23 | 15 |
| 23 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 34 | 20 |
| 24 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 11 |
| 25 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
Наем технического персонала для использования оборудования является обязанностью администрации МО.
- В каждой больнице, где имеется оборудование необходим технический специалист. Стоимость услуг техника составляет Ct=45000.
- Если в больнице
- один МРТ, то стоимость обслуживания C1=50000
- больше одного МРТ, то стоимость обслуживания C2=80000
- У администрации бюджет на это все PP=2000000
- Надо, чтобы в каждом районе был хоть один МРТ.
- Чем больше граждан приписаны к больнице, тем приоритетней больница для установки МРТ — больница, имеющая больше граждан, чем какая-то другая, не может иметь меньше МРТ.
- Общее число граждан, приписанных к больнице, деленное на количество МРТ в больнице не должно быть больше М=400000.
- С другой стороны, если больница не имеет собственного МРТ, необходимо распределить граждан этой больницы к другим, имеющим МРТ. Это грустно, и конечно, порождает недовольство, возможно гражданам теперь дольше добираться до новой больницы (в худшем случае, как раз на расстояние между старой и новой больницами).
- Но если граждане одной больницы переприписаны к другой, расстояние между этими больницами не должно превышать K=50 км (иначе совсем жестоко).
Задача состоит в том, чтобы минимизировать сумму «человеко-километров» по всем перемещенным в другие больницы гражданам.
Задача «Optprob/Управление скидками»
Мы должны купить N=1000 единиц товара. У нас есть три поставщика (A, B и C).
- Первый из них предлагает нам пропорциональную скидку: Три цены (pA1 $/единица, pA2 $/единица, pA3 $/единица), которые будут применяться ко всем единицам в зависимости от количества единиц, которые мы запрашиваем (pA1 > pA2 > pA3), у нас pA1=10, pA2=9, pA3=8. Рассмотрим, соответственно, три интервала: (0, A1], (A1, A2] и (A2, N], (A1=200, A2=5000).
- Второй предлагает нам инкрементную скидку: Три цены (pB1 $/единица, pB2 $/единица, pB3 $/единица, у нас pB1=9.5, pB2=9, PB3=8.5), которые применяются к единицам каждого интервала (pB1 > pB2 > pB3). Интервалы (0, B1], (B1, B2] и (B2, N], соответственно (B1=300, B2=700).
- Третий из них предлагает нам фиксированную цену pC $/единицу (pC=9) и фиксированные скидки: скидка в размере D1$ за заказ свыше C1 единиц и вторую скидку, которая добавляется к первой в размере D2$ при заказе свыше C2 единиц (C1=500, C2=800, D1=300, D2=300).
У кого сколько покупать, чтобы минимизировать стоимость покупки?
StasFomin 01:14, 28 ноября 2022 (UTC): Надо сделать модификацию задачи (генератор?), тут получились скучные цифры.
Задача «Optprob/Назначение инженеров на проекты»
Мы планируем распределять инженеров по проектам компании.
В течение следующего года компания имеет возможность участвовать в десяти инженерных проектах.
Каждый проект требует персонала (для проекта j потребуется Aj инженеров любого типа), приносит доход (G_j) и имеет общие расходы (C_j).
| Projects | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| A | 3 | 3 | 3 | 2 | 2 | 2 | 4 | 4 | 4 | 5 |
| C | 10000 | 20000 | 25000 | 40000 | 10000 | 40000 | 20000 | 25000 | 10000 | 30000 |
| G | 55000 | 60000 | 60000 | 90000 | 30000 | 100000 | 65000 | 50000 | 50000 | 60000 |
Инженеры компании делятся на две категории:
- S: Старший инженер (с опытом)
- JJ: Младший инженер (без достаточного опыта)
Каждый инженер имеет годовую зарплату M.
В настоящее время компания располагает штатом, состоящим из семи старших инженеров и четырех младших инженеров.
| Engineers | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| S | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 |
| JJ | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
| M | 50000 | 45000 | 30000 | 35000 | 28000 | 58000 | 36000 | 55000 | 35000 | 50000 | 33000 |
Каждый инженер, будь то старший или младший, подходит для каждого из проектов, в зависимости от их подготовки. Эта пригодность измеряется в виде непрерывного индекса от 0 (нет) до 1 (оптимально).
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| 1 | 0 | 1 | 0.5 | 0.5 | 0.5 | 1 | 0.3 | 0.2 | 0.4 | 0.8 |
| 2 | 0.5 | 0.5 | 1 | 0.3 | 0.2 | 0.4 | 1 | 1 | 0 | 0 |
| 3 | 1 | 1 | 0 | 0 | 1 | 0 | 0.4 | 0.5 | 0.6 | 0.5 |
| 4 | 2 | 0.5 | 0.5 | 1 | 0.3 | 0.2 | 0.4 | 2 | 0.3 | 0.5 |
| 5 | 0.5 | 1 | 0.3 | 0.2 | 0.4 | 1 | 1 | 1 | 0.3 | 0 |
| 6 | 0.2 | 0.5 | 0.5 | 3 | 0 | 0 | 1 | 1 | 1 | 0.6 |
| 7 | 1 | 0.6 | 0.7 | 0.5 | 0.5 | 1 | 0.3 | 0.2 | 0.4 | 0.6 |
| 8 | 1 | 3 | 3 | 3 | 0.5 | 1 | 0.3 | 0.2 | 0.4 | 1 |
| 9 | 0 | 1 | 1 | 0.5 | 0.5 | 1 | 0.3 | 0.2 | 0.4 | 0.1 |
| 10 | 0.5 | 1 | 0.3 | 0.2 | 0.5 | 1 | 0.3 | 0.2 | 0.4 | 1 |
| 11 | 0.5 | 1 | 0.3 | 0.2 | 0.5 | 1 | 0.3 | 0.2 | 0.4 | 1 |
Компания имеет возможность нанимать новых инженеров.
Затраты, которые компания оценивает для найма новых сотрудников, следующие
следующим образом:
- Старший инженер: $50 000/год
- Младшие инженеры: $35 000/год
Для новых инженеров компания присваивает пригодность 75% старшим инженерам и 50% младшим, так как персонал будет подбираться в соответствии к проектам.
Существует два типа назначений для инженеров:
- частичная занятость
- полный рабочий день
Компания позволяет назначить инженера на неполный или полный рабочий день на проекты. Если он работает полный рабочий день, он может быть занят только в одном проекте.
Если неполный рабочий день — может быть максимум в двух.
Новые инженеры могут быть назначены только эксклюзивно.
На проекте затраты на зарплату инженера, назначенного на неполный рабочий день, будут составлять половину ее оклада.
Количество инженеров, необходимых проекту, всегда является величиной, предполагающей исключительности.
Если инженеры назначены на неполный рабочий день, то два инженера на неполный рабочий день считаются как
один инженер.
Компания хочет, чтобы
- в каждом проекте, в котором она участвует, был как минимум один старший инженер (новый или уже работающий) на полную ставку.
- общая пригодность инженеров, назначенных на проект, была выше 50% — расчет общей пригодности производится как сумма пригодности инженеров, назначенных на проект, деленная на количество назначенных инженеров, независимо от того, работают ли они неполный или полный рабочий день.
Помимо всего этого, существуют и другие спецификации:
- В проекте не должно быть более трех инженеров, работающих неполный рабочий день.
- Проекты 5 и 6 не могут иметь ни одного общего инженера в этих двух проектах.
- Участие в проекте 2 на неполный рабочий день требует участия в проекте 3.
Цель компании — максимизация прибыли: «Доход от проектов» - «Расходы» (расходы на заработную плату + общие расходы).
- 📺видео📺
- * Код решения в проекте «adv2022-course-pyomo-business-optimization» в «optprob/Назначение_инженеров_на_проекты.ipynb»
Задача «Optprob/Иголка в стоге сена»
Создатель «теории ограничений» и пропагандист математической оптимизации в бизнес-задачах Элияху Моше Голдратт, часто прибегал к написанию «производственных бизнес-романов» для иллюстрации своих идей.
Очень рекомендую, для культуры, прочитать хотя бы первый и самый известный роман — «Цель»
В одном из них, в «Синдроме Стога Сена» на 40 страницах текста без малейшей романтики и лирики рассматривается в цифрах оптимизация некоторого модельного производства, и где «на пальцах» читателя убеждают, что для достижения максимальной прибыли нужно жертвовать локальными оптимумами, и принимать решения, часто интуитивно непонятные. Эту книгу десятилетия любят бизнес-тренеры, и консультанты, перерабатывают ее в тренинги…, см. например, тренинг Сергея Мартыненко или вот (→→→), свежий пост из бизнесового телеграмм-чата
Но если попробовать честно математически сформулировать эту задачу, выясняется, что даже сам Голдратт, пропустил оптимальное решение.
В докладе Стас Фомина была приведена модель на MathML и решение на GLPK (увы, вроде остались только слайды и видео), надо повторить это на Pyomo. Может где-то ее уже на Pyomo и решили (не проверял).
Всю книгу там перечитывать не обязательно, но если прочитаете — это будет совсем незря!
Задача «Optprob/Планирование задач с приоритетом и временами перенастройки»
Пусть имеется набор из n=10 производственных задач.
Каждая задача имеет время выполнения.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 12 | 14 | 25 | 10 | 13 | 18 | 7 | 9 | 11 | 18 |
Надо составить график выполнения заданий на производственном станке. Для этого устанавливаются n позиций в последовательности обработки, так что каждая задача должна быть назначена на позицию.
Кроме того:
- Между задачами существуют условные прецеденты: Задача i должна быть обработана после j, если задача t была обработана до i. Это собрано в бинарном атрибуте A_ijt.
| I | j | t |
| 1 | 2 | 3 |
| 4 | 6 | 3 |
| 3 | 10 | 8 |
| 8 | 7 | 1 |
| 10 | 5 | 8 |
- Между задачами нужна перенастройка станка. Если задача i находится на позиции k, а задача j — на позиции k + 1, добавляется дополнительное машинное время, s_ij.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| 1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 2 | 1 | 0 | 2 | 2 | 2 | 2 | 1 | 1 | 0 | 9 |
| 3 | 1 | 1 | 0 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 4 | 2 | 2 | 3 | 0 | 1 | 2 | 2 | 13 | 12 | 11 |
| 5 | 4 | 1 | 10 | 20 | 0 | 2 | 1 | 1 | 2 | 2 |
| 6 | 4 | 15 | 6 | 3 | 0 | 0 | 1 | 10 | 1 | 20 |
| 7 | 1 | 2 | 2 | 2 | 0 | 0 | 0 | 1 | 1 | 0 |
| 8 | 1 | 3 | 3 | 3 | 0 | 0 | 0 | 0 | 1 | 2 |
| 9 | 9 | 1 | 1 | 1 | 4 | 3 | 3 | 4 | 0 | 3 |
| 10 | 8 | 2 | 4 | 4 | 4 | 4 | 4 | 4 | 7 | 0 |
Цель задачи — минимизировать общее время производства.
Задача «Optprob/Группировка людей»
Пусть имеется группа из n=50 человек, с которыми будет создано m=10 рабочих групп.
Каждая группа будет состоять из фиксированного числа людей.
1 2 3 4 5 6 7 8 9 10 5 4 4 3 6 4 5 7 6 6
Некоторые люди знают друг друга.
| Known | |
|---|---|
| Person1 | Person2 |
| 1 | 2 |
| 1 | 3 |
| 1 | 4 |
| 2 | 6 |
| 2 | 8 |
| 3 | 6 |
| 4 | 6 |
| 4 | 7 |
| 4 | 23 |
| 4 | 27 |
| 4 | 30 |
| 5 | 10 |
| 5 | 15 |
| 5 | 20 |
| 6 | 18 |
| 7 | 40 |
| 7 | 45 |
| 7 | 48 |
| 8 | 10 |
| 8 | 12 |
| 8 | 26 |
| 8 | 28 |
| 9 | 19 |
| 9 | 20 |
| 10 | 11 |
| 10 | 35 |
| 10 | 45 |
| 11 | 21 |
| 11 | 29 |
| 12 | 41 |
| 12 | 42 |
| 13 | 46 |
| 14 | 47 |
| 14 | 49 |
| 14 | 50 |
| 15 | 30 |
| 15 | 32 |
| 16 | 38 |
| 16 | 45 |
| 17 | 23 |
| 17 | 24 |
| 18 | 29 |
| 19 | 39 |
| 21 | 30 |
| 22 | 40 |
| 22 | 41 |
| 23 | 43 |
| 24 | 34 |
| 24 | 36 |
| 25 | 37 |
| 26 | 39 |
| 27 | 40 |
| 28 | 41 |
| 29 | 41 |
| 30 | 42 |
| 31 | 32 |
| 32 | 34 |
| 33 | 35 |
| 34 | 38 |
| 35 | 39 |
| 36 | 41 |
| 37 | 44 |
| 38 | 44 |
| 39 | 45 |
| 40 | 41 |
| 40 | 42 |
| 41 | 46 |
| 42 | 47 |
| 43 | 48 |
Надо так распределить людей по группам (возможно будут лишние, это нормально), чтобы максимизировать число людей, которые всех знают в своей группе.
Задача «Optprob/Размещение административных учреждений»
Есть некий регион, с n=25 городами-поселками, который можно представить неориентированным графом дорожной связности, и стоит задача размещения там административных учреждений (МФЦ, госуслуги, и т.п.).
| Городок | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| Население | 16547 | 10269 | 9845 | 1987 | 1254 | 69845 | 3458 | 10059 | 35001 | 26987 | 13658 | 15874 | 6987 | 2657 | 4589 | 3547 | 875 | 945 | 11536 | 16895 | 12458 | 25478 | 50145 | 8450 | 6547 |
| Стоимость учреждения | 10000 | 10000 | 10000 | 5000 | 5000 | 10000 | 6400 | 9000 | 15000 | 47000 | 6500 | 19800 | 9000 | 9000 | 10000 | 10000 | 9000 | 9000 | 10000 | 10000 | 10000 | 10000 | 10000 | 6400 | 10000 |
- T
- лимит административных расходов на эти учреждения → 150000
- M
- сколько максимально населения можно приписать и обслуживать этим учреждением → 70000
- R
- если в городе больше R=25000, можно поставить два учреждения.
Учреждением можно обслуживать города в которых нет своих учреждений, приписал все население поселка к учреждению из другого города, но тогда этим людям придется ездить.
Как обычно, верхнетреугольная матрица расстояний (пусть в километрах)
| |
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 1 | 0 | 21 | 23 | 18 | 19 | 12 | 12 | 25 | 72 | 25 | 4 | 25 | 25 | 25 | 18 | 67 | 67 | 67 | 67 | 67 | 25 | 19 | 12 | 12 | 25 |
| 2 | 0 | 0 | 25 | 5 | 13 | 4 | 4 | 12 | 5 | 12 | 19 | 12 | 12 | 12 | 12 | 75 | 75 | 75 | 75 | 75 | 12 | 13 | 4 | 4 | 12 |
| 3 | 0 | 0 | 0 | 13 | 15 | 19 | 19 | 4 | 9 | 4 | 13 | 4 | 25 | 4 | 25 | 55 | 55 | 55 | 55 | 55 | 4 | 15 | 19 | 19 | 4 |
| 4 | 0 | 0 | 0 | 0 | 59 | 13 | 13 | 19 | 39 | 19 | 15 | 19 | 12 | 19 | 12 | 25 | 25 | 25 | 25 | 25 | 19 | 12 | 13 | 13 | 19 |
| 5 | 0 | 0 | 0 | 0 | 0 | 15 | 15 | 13 | 45 | 13 | 12 | 13 | 12 | 13 | 4 | 12 | 12 | 12 | 12 | 12 | 13 | 12 | 15 | 15 | 13 |
| 6 | 0 | 0 | 0 | 0 | 0 | 0 | 19 | 15 | 23 | 15 | 4 | 15 | 4 | 15 | 19 | 4 | 4 | 4 | 4 | 4 | 15 | 4 | 12 | 12 | 15 |
| 7 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 12 | 22 | 12 | 19 | 12 | 19 | 12 | 13 | 19 | 19 | 19 | 19 | 19 | 12 | 19 | 12 | 19 | 12 |
| 8 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 10 | 4 | 13 | 4 | 13 | 4 | 15 | 4 | 15 | 15 | 4 | 13 | 4 | 13 | 4 | 13 | 4 |
| 9 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 19 | 15 | 19 | 15 | 19 | 12 | 19 | 12 | 12 | 19 | 15 | 19 | 4 | 19 | 15 | 19 |
| 10 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 12 | 13 | 12 | 13 | 4 | 13 | 4 | 4 | 13 | 12 | 13 | 19 | 13 | 12 | 13 |
| 11 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 15 | 4 | 15 | 19 | 15 | 19 | 19 | 15 | 4 | 15 | 13 | 15 | 4 | 15 |
| 12 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 19 | 29 | 13 | 12 | 13 | 13 | 12 | 19 | 12 | 15 | 12 | 19 | 25 |
| 13 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 43 | 15 | 4 | 15 | 15 | 4 | 13 | 4 | 12 | 15 | 13 | 12 |
| 14 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 12 | 19 | 24 | 12 | 19 | 15 | 19 | 4 | 12 | 15 | 4 |
| 15 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 13 | 36 | 4 | 13 | 4 | 13 | 19 | 11 | 78 | 19 |
| 16 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 15 | 19 | 15 | 19 | 15 | 13 | 77 | 49 | 13 |
| 17 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 13 | 32 | 13 | 4 | 15 | 12 | 29 | 15 |
| 18 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 23 | 15 | 19 | 4 | 4 | 43 | 12 |
| 19 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 25 | 13 | 19 | 19 | 9 | 4 |
| 20 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 15 | 13 | 13 | 11 | 19 |
| 21 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 15 | 15 | 12 | 13 |
| 22 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 12 | 23 | 15 |
| 23 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 34 | 20 |
| 24 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 11 |
| 25 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
Надо, в рамках выданного бюджета, расставить учреждения по поселкам-городкам так, чтобы сумма человеко-километров по тем, кому не достанется своих учреждений (считаем, что внутри поселков добираются до своих чиновников мгновенно), была минимальной.
Задача «Optprob/Домостроительство»
Застройщик хочет оптимизировать использование прямоугольной площади микрорайона, который он выбил для жилищного строительства.
Площадь блока составляет 25000 м2 (500м в длину на 50м в ширину).
Он собирается построить дома в два ряда (длина каждого ряда 500 м, ширина 20 м) — ну такой классический американский минигородок с одной улицей (симпсоны, саус-парк).
В середине есть участок шириной 10 м для улицы-проезда.
Застройщик должен решить сколько домов построить в каждом ряду в рамках трех моделей:
- Элитка
- Отдельные элитные такие дома на участках площадью 400м2 (20м в длину 20м в ширину).
- Таунхаус
Совмещенные блоки из двух домов на участках площадью 700м2 (35м в длину 20м в ширину).
- Эконом-пенал
- Небольшие, но раздельные эконом-домики на участках площадью 200м2 (10м в длину 20м в ширину) для каждого дома.
Стоимость строительства каждого дома равна
190000 150000 100000
Цена продажи для каждого типа дома составляет
250000 200000 120000
Городской совет устанавливает минимальное количество домов каждого типа,
4 4 6
- если количество таунхаус-блоков больше, чем количество элитных домов, это влечет за собой дополнительные расходы в размере CA=15000 на каждый дополнительный двухдомный блок.
- «Эконом-пенал» дома могут располагаться только в одном ряду (из двух, требования архитектора).
- Установленный потолок инвестиций составляет TI=3000000 долларов.
- Инвестиционные деньги имеют стоимость CI=3%.
- Застройщик не обязан строить весь ряд — можно строить дома в упор друг-другу, или с промежутками, или вовсе не до конца.
Предложите модель, которая максимизирует выгоду.
- Код решения в проекте «adv2022-course-pyomo-business-optimization» в «optprob/Домостроительство.ipynb»
- 📺видео📺
Задача «Optprob/Назначение студентов в группы»
После получения оценок первой оценки ВУЗ рассматривает вопрос об улучшении успеваемости своих учеников по математике.
- Оценка каждого ученика по этому предмету известна, от 0 до 10.
- Закон о персданных конечно запрещает узнать (нам, оптимизаторам) у кого какая оценка, даже под «анонимным номером», но известно, что после разбития на категории, у нас такое грубое распределение студентов:
- v=1, «неудовлетворительно [0-5]» → 24
- v=2, «хорошо» [5,7], → 58
- v=3, «отлично» [7,9], → 11
- v=4, «блестяще» [9,10] → 7
ВУЗ решил создать учебные группы с целью, чтобы ученики с худшими оценками были связаны с учениками с лучшими оценками.
- Для этого, создается 15 учебных групп.
- В каждой группе может быть не более 10 учеников.
- В каждой группе по возможности нужно поместить ученика с «блестящей» оценкой.
- Если в группе нет «блестящих», в ней должно быть по крайней мере, не меньше отличников, чем и в любой группе с «блестящими».
- У группы есть «уровень» , где
x_{ij} — число студентов «уровня i» назначенных в группу «j» — мы, оптимизаторы, работаем только с «уровнями» и «группами», не с отдельными студентами.
Цель состоит в том, чтобы сбалансировать уровень оценок групп, чтобы разница минимального и максимального «уровня» у групп было минимальным.
- Код решения в проекте «adv2022-course-pyomo-business-optimization» в «optprob/Назначение_студентов_в_группы.ipynb»
- Blog:Advanced_Algorithms/Разбор_задачи_«Назначение_студентов_в_группы»
Задача «Optprob/Управление загрязняющими продуктами»
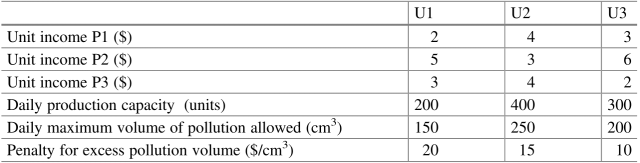
Компания рассматривает возможность производства трех своих продуктов P1, P2 и P3 в одном из мест U1, U2 и U3.
При производстве каждого продукта образуется объем загрязнения в объеме 0,5, 2 и 1 см3, соответственно, на единицу произведенной продукции, независимо от местоположения.
В таблице показаны для каждого из мест:
- удельный доход ($) от каждого продукта,
- суточная производственная мощность (единиц).
- дневная производственная мощность (единиц),
- максимальные объемы загрязнения (см3),
- штраф за превышение объема загрязнения ($/см3).
Компания, осознавая экологические проблемы, предлагает цели с порядком приоритетов:
- Приоритет 1. Максимизировать ежедневный доход.
- Приоритет 2. Не превышать максимальный уровень загрязнения местности.
- Приоритет 3. Компания не хочет тратить более $9000 в день из-за превышения уровня загрязнения.
Давайте сформулируем модель, которая позволит нам определить, сколько ежедневных единиц каждого продукта должно быть произведено и в каком месте.
Задача «Optprob/Производство подразделяемых задач»
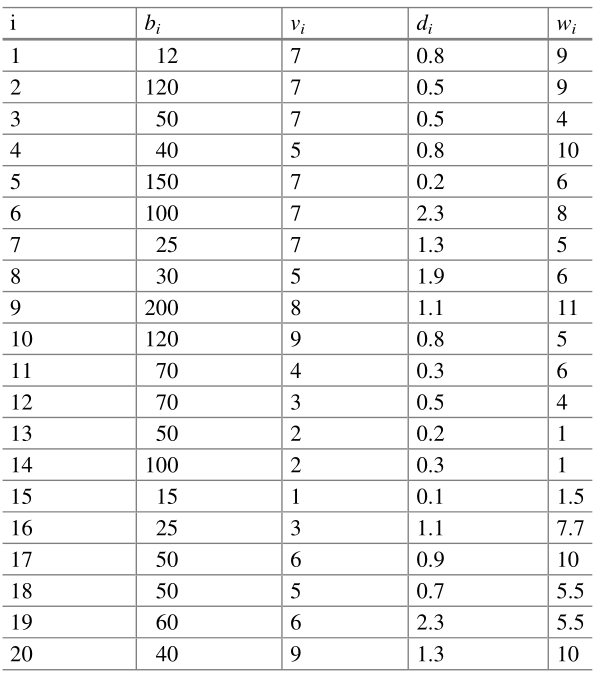
Дано множество из n=15 производственных задач, каждая из которых имеет…
| Tasks | |
|---|---|
| Id | Time |
| 1 | 12 |
| 2 | 4 |
| 3 | 11 |
| 4 | 3 |
| 5 | 23 |
| 6 | 12 |
| 7 | 5 |
| 8 | 3 |
| 9 | 23 |
| 10 | 34 |
| 11 | 23 |
| 12 | 23 |
| 13 | 21 |
| 14 | 56 |
| 15 | 45 |
Имеется набор 5 машин для обработки заданий.
- Все задачи должны быть обработаны.
- Задание считается обработанной, если сумма времени обработки на каждой машине равна времени выполнения задания.
- Задание может быть частично обработано не более чем на трех машинах, но всегда одна машина должна обрабатывать не менее одной трети времени выполнения задания.
- Каждое задание, которое обрабатывается на любой машине, приводит к тому, что машина затрачивает время на установку TT=100 плюс время, которое машина обрабатывает задание.
Надо сбалансировать распределение задач на машины, чтобы минимизировать время той машины, которая работает больше всего.
Для простоты: Нет необходимости учитывать перекрытие: то есть, нет необходимости
контролировать или решать, когда задача обрабатывается на машине.
- Код решения в проекте «adv2022-course-pyomo-business-optimization» в «optprob/Производство_подразделяемых_задач.ipynb»
- Участник:PankratovViktor/Производство подразделяемых задач
Задача «Optprob/Хранение артефактов на складе»
Представим склад на котором надо хранить какие-то артефакты.
На складе есть m мест хранения, каждое из которых поддерживает определенный вес.
- m
- 15
Максимальный вес для места:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 15 | 25 | 25 | 30 | 30 | 40 | 40 | 30 | 30 | 25 | 25 | 15 | 15 | 10 | 10 |
Между местами также есть расстояние, и есть (антипожарно-антимагическое) правило, что между любыми двумя занятыми местами хранения, должно быть не меньше 3х метров.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | |
| 1 | 0 | 10 | 2 | 1 | 1.5 | 2.5 | 3.5 | 4 | 5 | 5.5 | 6 | 6.5 | 7 | 7.7 | 7 |
| 2 | 0 | 0 | 1.5 | 2 | 1.5 | 3 | 4 | 5 | 2 | 3 | 2 | 3 | 4 | 5 | 5 |
| 3 | 0 | 0 | 0 | 1.5 | 4 | 1.5 | 1.5 | 4 | 2 | 2 | 2 | 2 | 5 | 3 | 2 |
| 4 | 0 | 0 | 0 | 0 | 2 | 4 | 4 | 1.5 | 4 | 2 | 2 | 1 | 1 | 1 | 1 |
| 5 | 0 | 0 | 0 | 0 | 0 | 3 | 4 | 2 | 1 | 2 | 2 | 2 | 2 | 3 | 2.5 |
| 6 | 0 | 0 | 0 | 0 | 0 | 0 | 3.5 | 2.5 | 1 | 2 | 1 | 4.6 | 1 | 2.7 | 4 |
| 7 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 2 | 1 | 2.6 | 1 | 2.7 | 1.5 | 1.5 |
| 8 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 3 | 4 | 6 | 3.5 | 2.5 |
| 9 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 2 | 1 | 2.6 | 1 | 2.7 |
| 10 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 2 | 1 | 1.5 | 2.5 |
| 11 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 3.4 | 3.5 | 2.7 |
| 12 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 4 | 2.5 | 1 |
| 13 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 2.5 | 2 |
| 14 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 3 |
| 15 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
Есть n=25 артефактов.
Вес артефактов:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 12 | 14 | 15 | 16 | 4 | 7 | 5 | 9 | 12 | 15 | 14 | 13 | 12 | 17 | 3 | 5 | 7 | 6 | 3 | 4 | 5 | 5 | 3 | 2 | 2 |
Некоторые артефакты совместимы — и их можно размещать в одном месте хранения, если суммарный вес не превышен.
Некоторые нельзя — таблица совместимости (1=совместимы), представлена ниже.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | |
| 1 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 1 |
| 2 | 0 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 |
| 3 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| 4 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 |
| 5 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 |
| 6 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 |
| 7 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 8 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| 9 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 |
| 10 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 11 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 |
| 12 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 0 |
| 13 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 14 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 |
| 15 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| 16 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 17 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 |
| 18 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 19 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 20 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 |
| 21 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 |
| 22 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| 23 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 24 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| 25 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
Не факт, что вообще удастся разместить все артефакты (ну тогда лишние уедут на другие «Хранилища»), но цель — разместить максимум артефактов (в штуках), т.е. каждому артефакту назначить место, или отказать в хранении.
Задача «Optprob/Аренда склада»
Предприниматель хочет арендовать ряд промышленных зданий на следующий год для бизнеса по продаже цемента.
В промышленной зоне, где он собирается открыть бизнес, есть шесть складов («i= 1…6»), доступных для аренды.
Бизнесмен начинает бизнес с 50 тонн цемента и пяти автомобилей для транспортировки.
Склады, которые он арендует, должны вмещать как цемент, так и
транспортные средства.
Промышленные здания предлагают емкости для хранения цемента и собранных транспортных средств, понятно, что хранить можно либо цемент, либо автомобили, ну и стоимость аренды разная.
| Номер склада | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| Стоимость аренды | 35 | 33 | 26 | 23 | 30 | 29 |
| Вместимость машин | 2 | 2 | 2 | 1 | 3 | 3 |
| Вместимость цемента | 20 | 18 | 13 | 19 | 22 | 22 |
Цель состоит в том, чтобы минимизировать общую стоимость аренды на этот год.
Задача «Optprob/Распределение рабочих по производственным центрам»
- Есть L городов
- Есть n рабочих.
- Каждый работник живет в определенном городе.
- Есть m рабочих центров, каждый из которых
- расположен в определенном городе.
- имеет минимальную и максимальную потребность в работниках.
Надо так назначить работников к производственным центрам, чтобы минимизировать полное расстояние, которое проезжают эти рабочие.
| L | 25 |
| m | 40 |
Сколько работников в каждом городе?
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | |
| n | 4 | 8 | 16 | 13 | 10 | 12 | 11 | 10 | 7 | 7 | 7 | 5 | 5 | 3 | 2 | 2 | 1 | 1 | 1 | 2 | 1 | 1 | 2 | 3 | 4 |
Расстояние между 25 городами (расстояния симметричные, представлены верхней треугольной матрицей).
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | |
| 1 | 0 | 21 | 23 | 18 | 19 | 12 | 12 | 25 | 72 | 25 | 4 | 25 | 25 | 25 | 18 | 67 | 67 | 67 | 67 | 67 | 25 | 19 | 12 | 12 | 25 |
| 2 | 0 | 0 | 25 | 5 | 13 | 4 | 4 | 12 | 5 | 12 | 19 | 12 | 12 | 12 | 12 | 75 | 75 | 75 | 75 | 75 | 12 | 13 | 4 | 4 | 12 |
| 3 | 0 | 0 | 0 | 13 | 15 | 19 | 19 | 4 | 9 | 4 | 13 | 4 | 25 | 4 | 25 | 55 | 55 | 55 | 55 | 55 | 4 | 15 | 19 | 19 | 4 |
| 4 | 0 | 0 | 0 | 0 | 35 | 13 | 13 | 19 | 39 | 19 | 15 | 19 | 12 | 19 | 12 | 25 | 25 | 25 | 25 | 25 | 19 | 12 | 13 | 13 | 19 |
| 5 | 0 | 0 | 0 | 0 | 0 | 15 | 15 | 13 | 45 | 13 | 12 | 13 | 12 | 13 | 4 | 12 | 12 | 12 | 12 | 12 | 13 | 12 | 15 | 15 | 13 |
| 6 | 0 | 0 | 0 | 0 | 0 | 0 | 35 | 15 | 23 | 15 | 4 | 15 | 4 | 15 | 19 | 4 | 4 | 4 | 4 | 4 | 15 | 4 | 12 | 12 | 15 |
| 7 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 12 | 22 | 12 | 19 | 12 | 19 | 12 | 13 | 19 | 19 | 19 | 19 | 19 | 12 | 19 | 12 | 19 | 12 |
| 8 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 10 | 4 | 13 | 4 | 13 | 4 | 15 | 4 | 15 | 15 | 4 | 13 | 4 | 13 | 4 | 13 | 4 |
| 9 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 19 | 15 | 19 | 15 | 19 | 12 | 19 | 12 | 12 | 19 | 15 | 19 | 4 | 19 | 15 | 19 |
| 10 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 12 | 13 | 12 | 13 | 4 | 13 | 4 | 4 | 13 | 12 | 13 | 19 | 13 | 12 | 13 |
| 11 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 15 | 4 | 15 | 19 | 15 | 19 | 19 | 15 | 4 | 15 | 13 | 15 | 4 | 15 |
| 12 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 19 | 29 | 13 | 12 | 13 | 13 | 12 | 19 | 12 | 15 | 12 | 19 | 25 |
| 13 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 43 | 15 | 4 | 15 | 15 | 4 | 13 | 4 | 12 | 15 | 13 | 12 |
| 14 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 12 | 19 | 24 | 12 | 19 | 15 | 19 | 4 | 12 | 15 | 4 |
| 15 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 13 | 36 | 4 | 13 | 4 | 13 | 19 | 11 | 78 | 19 |
| 16 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 15 | 15 | 19 | 15 | 19 | 15 | 13 | 77 | 49 | 13 |
| 17 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 13 | 32 | 13 | 4 | 15 | 12 | 29 | 15 |
| 18 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 23 | 15 | 19 | 4 | 4 | 43 | 12 |
| 19 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 25 | 13 | 19 | 19 | 9 | 4 |
| 20 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 15 | 13 | 13 | 11 | 19 |
| 21 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 15 | 15 | 12 | 13 |
| 22 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 12 | 23 | 15 |
| 23 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 34 | 20 |
| 24 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 11 |
| 25 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
Рабочие центры.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | |
| Минимальная потребность | 2 | 3 | 2 | 3 | 4 | 2 | 3 | 4 | 2 | 3 | 4 | 2 | 3 | 4 | 2 | 2 | 2 | 2 | 2 | 3 | 4 | 2 | 2 | 2 | 2 | 3 | 4 | 2 | 2 | 2 | 2 | 3 | 4 | 2 | 2 | 2 | 2 | 4 | 5 | 5 |
| Максимальная потребность | 5 | 5 | 5 | 5 | 7 | 4 | 4 | 6 | 4 | 5 | 7 | 4 | 4 | 5 | 5 | 4 | 4 | 4 | 4 | 5 | 6 | 4 | 4 | 4 | 4 | 4 | 6 | 4 | 4 | 4 | 4 | 5 | 7 | 5 | 4 | 4 | 4 | 6 | 7 | 7 |
| Город для рабочего центра | 1 | 1 | 2 | 2 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 8 | 9 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 17 | 17 | 18 | 18 | 19 | 19 | 20 | 20 | 20 | 21 | 22 | 22 | 23 | 23 | 24 | 24 | 25 | 25 |
Задача «Optprob/Покупка станков»
Задан набор из n=40 производственных задач, каждая из которых имеет заданное время обработки.
Стоимость станков, которые выполняют задачи, составляет C=400 за каждый.
- каждое задание обрабатывается на одном станке (не параллелится)
- и станок не может обрабатывать более пяти задач (M) за раз, в день, без отдыха.
Надо:
- чтобы все задачи обрабатывались менее чем за TT=8 ч (машины начинают работать одновременно, и нет задач продолжительностью более 8 ч).
- минимальную стоимость покупки станков.
- Код решения в проекте «adv2022-course-pyomo-business-optimization» в «optprob/Покупка_станков.ipynb»
- Blog:Advanced_Algorithms/Хорошие_практики_компактных_Pyomo-формулировок_на_примере_решения_«Задачи_о_станках»
- Участник:Cherniavskii/BusinessProblems/Покупка_станков
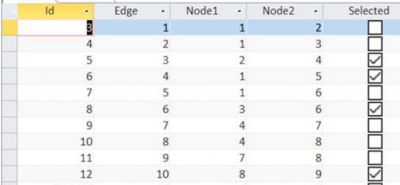
Задача «Optprob/Независимое множество ребер»
Дан неориентированный граф G (N, E), надо получить множество с наибольшим числом несвязанных ребер (два ребра соединяются, когда они разделяют узел).
- 📺видео📺
- * Код решения в проекте «adv2022-course-pyomo-business-optimization» в «optprob/Независимое_множество_ребер.ipynb»
Задача «Optprob/Поделить поровну»
Задан набор из n элементов, каждый из которых целое положительное число.
S = {7 8 2 5 7 1 5 5 9 9 4 3 2 2 1 3 6 3 11 12}
Как поделить их на две максимально равные части?
Задача «Optprob/Капитальные инвестиции»
У нас есть 2200 долларов, которые можно инвестировать в течение следующих 5 лет.
В начале каждого года мы можем инвестировать часть денег в депозиты сроком на 1 или 2 года.
По годичным депозитам выплачивается 5% годовых, в то время как по 2-летним депозитам выплачивается 11% в конце 2-х лет.
Кроме того, в начале второго года можно вложить деньги в 3-летние облигации компании А, общая доходность которых составляет 17%.
Куда и сколько инвестировать? Добейтесь того, в конце пятилетнего периода капитал был как можно больше.
Задача «Optprob/Портфель ценных бумаг»
Инвестор владеет долями в различных ценных бумагах.
Более конкретно, он владеет b акций некоторых ценных бумаг
Текущие цены этих ценных бумаг равны
Допустим, что можно предсказать дивиденды, которые будут выплачены в конце начинающегося года, и окончательные цены различных ценных бумаг;
то есть ценная бумага
Наша цель — скорректировать наш портфель, то есть количество акций в каждой ценной бумаге, которые будут куплены и проданы по текущей цене, таким образом, чтобы дивиденды были максимизированы.
Необходимо обеспечить выполнение определенных условий, которым должен удовлетворять хорошо сбалансированный портфель,
таких как:
- Общий капитал портфеля не должен изменяться при корректировке; то есть общий капитал, который покупается, такой же, как и проданный.
- Портфель должен избегать чрезмерной зависимости от какой-либо одной ценности. Это условие может быть установлено путем требования, чтобы капитал, связанный с какой-либо конкретной ценной бумагой, после корректировки покупки и продажи составлял по меньшей мере определенный процент r% от текущего общего капитала портфеля.
- Общий капитал в будущем должен составлять не менее текущего капитала плюс определенный процент s% от инвестированного в настоящее время капитала.
Для нашей задачи положим r=3%; s=5%;
Задача «Optprob/Продажа фруктов»
Торговцу фруктами нужно
- 16 коробок апельсинов,
- 5 коробок бананов
- 20 коробок яблок.
Он пользуется услугами оптовиков, которые в состоянии удовлетворить его потребности, но продают фрукты только в полных контейнерах.
Оптовик А отправляет в каждом контейнере по
- 8 коробок апельсинов,
- 1 коробку бананов и
- 2 коробки яблок.
Оптовый продавец B отправляет
- 2 коробки апельсинов,
- одну коробку бананов,
- 7 коробок яблок в каждом контейнере.
Зная, что оптовик А находится в 150 км, а оптовик В - в 300 км, подсчитайте, сколько контейнеров нам придется купить у каждого оптовика, чтобы сэкономить время и свести к минимуму расстояние (каждый контейнер означает поездку).
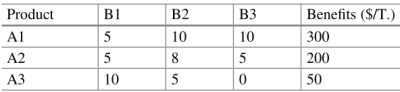
Задача «Optprob/производство продукта»
Компания располагает
- 1000 тоннами минерала В1,
- 2000 тоннами минерала В2
- 500 тоннами B3.
Из этих материалов могут быть получены продукты A1, A2 и A3.
Компания хочет определить количество каждого продукта, которое должно быть произведено, чтобы получить максимальную экономическую выгоду от операции.
Далее подробно указывается необходимое количество каждого минерала для получения 1 тонны каждого
продукта и польза, получаемая от каждого из них.
Компания также должна учитывать:
- что он не должен производить более 10 тонн А2, поскольку на рынке не так много спроса.
- что есть компания, которая покупает минерал В2 по цене 20 долларов за тонну.
Максимизируйте прибыль компании.




























[ Хронологический вид ]Комментарии
Войдите, чтобы комментировать.